Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 6 - Circle

Let O be the centre of the circle.

AB = 12 cm

OC = 12 cm

OC ⊥ AB

As we know that,

Perpendicular drawn from the centre of the circle to the chord, bisects the chord.

So, AC = 6cm

In ∆ OCA,

OC²+AC² = AO²

∴8²+6² = AO²

∴AO² = 100

∴AO = 10

Thus, AO 10 cm

Diameter = 2 x 10 cm = 20 cm.

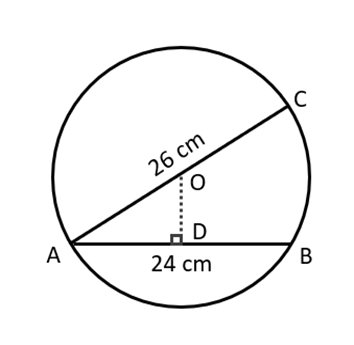
We have given that,

Diameter = 26 cm

Chord = 24 cm

Perpendicular drawn from the centre of the circle to the chord bisects the chord.

OD ⊥ AB

So, AD = DB

AO = OC ………………………(radius of circle)

In ∆ ODA,

OD² + AD² = OA²

∴OD² + 12² = 13²

∴OD² + 144 = 169

∴OD² = 169-144 = 25

∴OD = 5 cm

Thus, the distance of the chord from the centre is 5 cm.

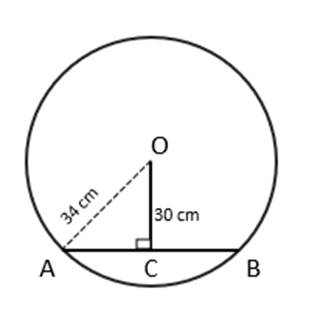
Let the chord be AB.

O be the centre of the circle.

OC be the perpendicular drawn from the centre to the chord AB.

We know that,

perpendicular drawn from the centre of the circle to the chord bisects the chord.

So, OC ⊥ AB.

In ∆ OCA,

OC² + AC² = OA²

∴30² + AC² = 34²

∴900 + AC² = 1156

∴AC² = 256

∴AC = 16 cm

Thus, AB = 2 x AC = 2 x 16 = 32

∴ The length of the chord is 32 cm.

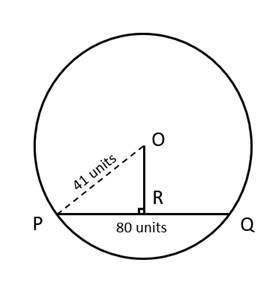
We know that,

perpendicular drawn from the centre of the circle to the chord bisects the chord.

∴ PR = RQ = 40 unit

In ∆ OPR.

OR² + PR² = OP²

∴ OR² + 40² = 41²

∴ OR² = 1681 - 1600

∴ OR² = 81

∴ OR = 9 unit

Thus, the distance of the chord from the centre of the circle is 9 units.

Draw a perpendicular from O to line AB.

So,

OC ⊥ PQ and OC ⊥ AB

We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.

So,

PE = EQ .....(1)

and

AE = EB .....(2)

Now, equation (2) - equation (1)

AE - PE = EB - EQ

∴AP=BQ

Hence proved

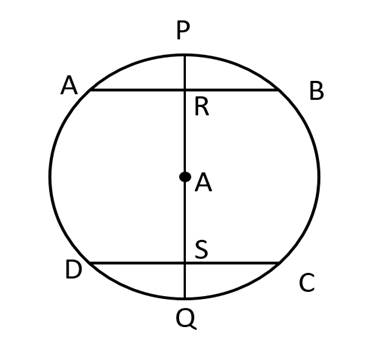
Let AB and CD be the two chords of the circle. The centre of the circle be O through which the diameter PQ passes.

Let the diameter PQ bisect the two chords and point R and S.

We know that the when the line passing through the centre of the circle bisects the chord then the line is perpendicular to the chord.

Thus, ∠ARS = ∠DSR = 90°

AB will be thus parallel to CD and cut by the transversal PS as interior angle on the same side of the transversal are equal.

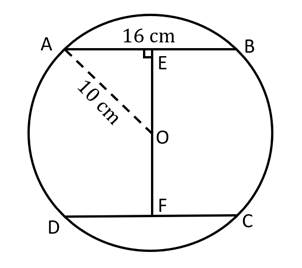
Let AB and CD be the two chords.

AB = CD = 16 cm

Radius = AO = 10 cm

Let OE be the perpendicular drawn from the Centre of the circle to the chord AB.

Perpendicular drawn from the Centre of the circle to the chord bisects the chord.

So, AE = EB = 8 cm

In Δ ΑΕΟ,

EO² + AE² = AO²

∴ EO² + 8² = 10²

∴ EO² = 100 - 64

∴ EO² = 36

∴ EO = 6 cm

We know that,

congruent chords of a circle are equidistant from the Centre.

So,

EO = OF = 6 cm

Distance of these chords from the Centre is 6 + 6 = 12 cm.

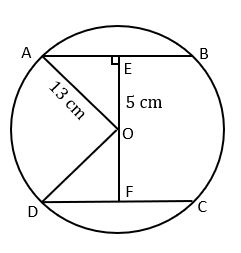
Let the two chords be AB and CD.

Radius = AO = 13 cm

Let OE be the perpendicular drawn from the centre of the circle to the chord AB.

Perpendicular drawn from the centre of the circle to the chord bisects the chord.

So, AE = EB

In Δ ΑΕΟ,

EO² + AE² = AO²

∴ 5²+ AE² = 13²

∴ AE² + 25 = 169

∴ AE² = 144

∴ AE = 12 cm

And AE = EB = 12 + 12 = 24 cm

Thus, AB = CD = 24 cm as chords of a circle equidistant from the centre are congruent.

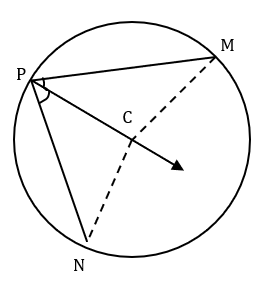
Join CN and CM.

In Δ CPN and Δ CPM,

PM ≅ PN………………………..(Given)

PC = PC…………………………(Common)

CN = CM………………………..(Radius)

Thus, Δ CPN ≅ Δ CPM ….….(By SSS congurency)

So, ∠ CPN = ∠ CPM………..(CPCT)

Thus, ray PC is the bisector of ∠NPM.

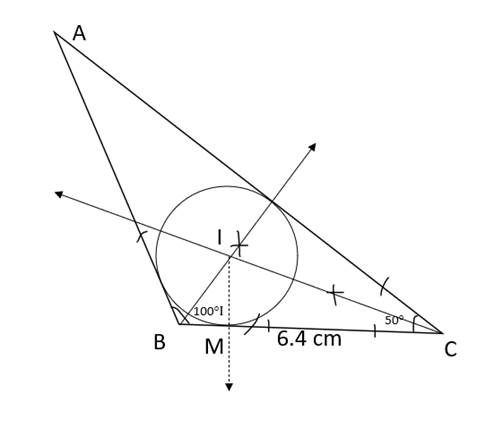
Steps of construction:

1. Draw ABC of given measures.

2. Draw angle bisectors of B and C

3. Name the point of intersection of angle bisectors as I.

4. Draw a perpendicular IM on side BC. Point M is the foot of the perpendicular

5. With I as center and IM as radius, draw a circle that touches all sides of the triangle.

By angle sum property of triangles,

In ∆ PQR

∠P + ∠Q + ∠R = 180°

70° + ∠Q + 50 ° = 180°

∠Q= 60°

Steps of construction:

1. Draw a line QR = 7.3 cm.

2. With Q as centre, draw an angle of 60° using the protractor. Similarly, draw an angle of 50% with R as centre. Where the rays RY and XQ meet, name the point as P. Thus, ∆ PQR is obtained.

3. Draw the perpendicular bisectors of the lines PR and QR.

Let these perpendicular bisectors meet at point 0.

4. With O as centre and OP as radius, construct a circle touching all the vertices of the A PQR This circle is thus the required circumcircle.

Steps of construction:

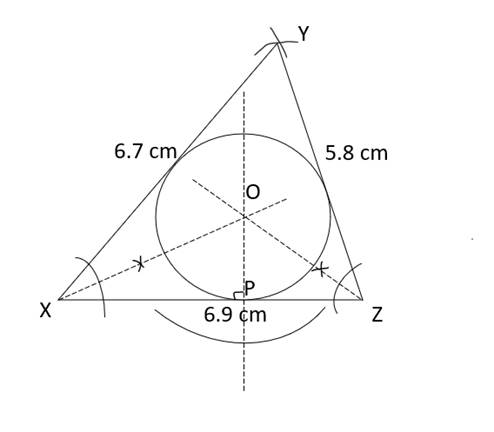
1. Draw XZ 6.9 cm

2. With X as centre and 6.7 cm as radius, draw an arc above the line XZ Also, with Z as centre and 5.8 cm as radius, draw an arc cutting the previous drawn arc at point Y. A XYZ is thus obtained.

3. Construct the angle bisectors of ∠X and ∠Z and let them meet at point 0.

4. Through point O, draw a perpendicular to line XZ. Let the perpendicular meet the line XZ at point P

5. With O as centre and OP as radius, draw a circle inside the ∆XYZ

This is the required incircle.

Steps of construction:

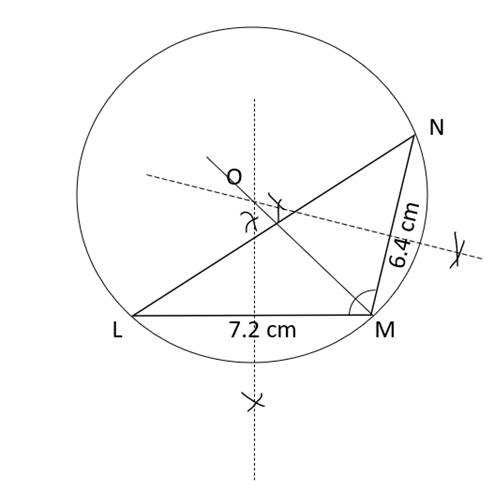
1. Draw a line LM = 7.2 cm.

2. With M as centre, draw an angle of 105° using the protractor.

3. With M as centre and 6.4 cm as radius, cut an arc on ray MX and name it as N.

4. Join LN. A LMN is thus obtained.

5. Draw the perpendicular bisectors of the lines NM and LM. Let these perpendicular bisectors meet at point O.

4. With O as centre and OM as radius, construct a circle touching all the vertices of the ∆LMN.

This circle is thus the required circumcircle.

Steps of construction:

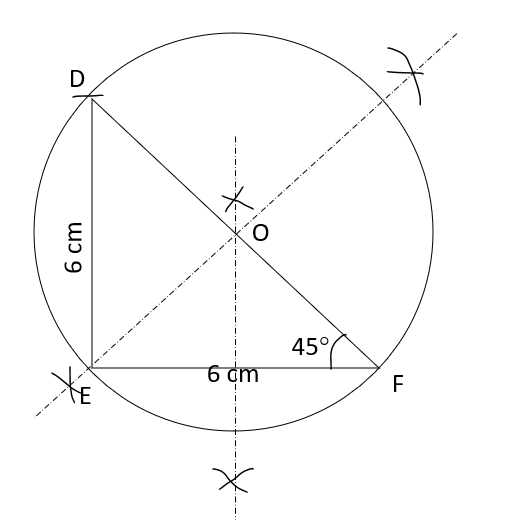
1. Draw a line EF 6 cm.

2. With F as centre, draw an angle of 45° using the protractor

3. With E as centre and 6 cm as radius, cut an arc on ray FX and name it as D.

4. Join DE ∆DEF is thus obtained

5. Draw the perpendicular bisectors of the lines DF and EF Let these perpendicular bisectors meet at point 0.

6. With O as centre and OE as radius, construct a circle touching all the vertices of the A DEF This circle is thus the required circumcircle.

Let the chord be AB.

O be the centre and OC be the perpendicular drawn from the centre of the circle to the chord AB

Perpendicular drawn from the centre of the circle to the chord bisects the chord.

AC = CB

OA is the radius = 10 cm

In ∆ OAC

OC² + AC² = OA²

6² + AC² = 10²

36+ AC² = 100

AC² = 64

AC = 8 cm

AC = CB = 8 cm

AB = AC+ CB = 8 + 8 = 16 cm

Hence, the correct answer is option A

(C) Incentre

(A) Circumcircle

The circle which passes through all vertices of a triangle is called circumcircle.

Let the chord be AB = 24 cm

Distance of the chord from the centre O is 5 cm.

AO is the radius of the circle.

Perpendicular from the centre of the circle to the chord bisects the chord.

So, AC = CB

In ∆AOC,

OC² + AC² = AO²

5² + 12² = AO²

AO² = 25 + 144 = 169

AO = 13 cm

Thus, the radius of the circle is 13 cm.

The longest chord of the circle is the diameter.

Radius 2.9 cm.

So, diameter 2.9 + 2.9 = 5.8 cm

Radius = 4 cm

OP = 4.2 cm

OP will be thus outside the circle as it is greater than the radius.

Let the chords be AB = 6 cm and CD = 8 cm

O be the centre with OA= OC = 5 cm as radius.

OE ⊥ AB and OF ⊥ CD.

In ∆ AEO,

AE² + EO² = AO²

3²+ EO² = 5²

9 + EO² = 25

EO² = 16

EO = 4 cm

Similarly, in In ∆OFC,

OF²+ CF2²= OC²

OF²+ 4² = 5²

OF² + 16 = 25

OF² = 9

OF = 3 cm

Thus, the distance between the two chords is,

EO + OF = 4 + 3 cm = 7 cm.

Steps of construction:

1. Draw a line SP = 7.5 cm.

2. With S as centre and 7.5 cm as radius, draw an arc above the line SP.

3. With P as centre and 7.5 cm as radius, cut an arc on on the previous drawn arc and name the point of intersection as D.

4. Join DS and DP. ∆ DSP is thus obtained.

5. Draw the perpendicular bisectors of the lines DP and SP. Let these perpendicular bisectors meet at point 0.

4. With O as centre and OP as radius, construct a circle touching all the vertices of the ∆ DSP.

This circle is thus the required circumcircle.

Radius = 4 cm

Steps of construction

1. Draw a line SP = 7.5 cm.

2. With S as centre and 7.5 cm as radius, draw an arc above the line SP.

3. With P as centre and 7.5 cm as radius, cut an arc on on the previous drawn arc and name the point of intersection as D.

4. Join DS and DP. ∆DSP is thus obtained.

5. Draw the angle bisectors of angle S and P and let them meet at point O.

6. Draw the perpendicular from point O to the line SP. Join OA.

7. With O as centre and OA as radius, draw a circle touching all the sides of the triangle.

This is the required incircle.

Radius = 2 cm

ratio of radius of circumcircle to the radius of incircle = 4 : 2 = 2 : 1

Steps of construction:

1. Draw a line ST = 7.5 cm.

2. With T as centre draw an angle ∠ STX = 110°.

3. With T as centre and 5.7 cm as radius, cut an arc on XT and name the point of intersection as N.

4. Join SN. ∆ NTS is thus obtained.

5. Draw the perpendicular bisectors of the lines ST and NT. Let these perpendicular bisectors meet at point O.

4. With O as centre and OT as radius, construct a circle touching all the vertices of the ∆ NTS.

This circle is thus the required circumcircle.

Steps of construction:

1. Draw a line ST = 7.5 cm.

2. With T as centre draw an angle ∠STX = 110°.

3. With T as centre and 5.7 cm as radius, cut an arc on XT and name the point of intersection as N.

4. Join SN. ∆NTS is thus obtained.

5. Draw the angle bisectors of angle S and T and let them meet at point O.

6. Draw the perpendicular from point O to the line ST. Join OP.

7. With O as centre and OP as radius, draw a circle touching all the sides of the triangle.

This is the required incircle.

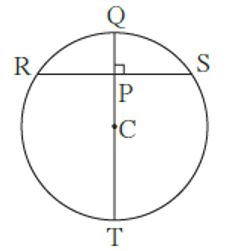
Join RC and CS.

Perpendicular drawn from the centre of the circle to the chord bisects the chord.

So, RP = PS

In ∆ RPC,

RP² + PC² = RC²

RP² +5² = 13²

RP² = 169 - 25 = 144

RP = 12 cm

Thus, RP = PS = 12 cm

So, RS = RP + PS = 12+12 + 24 cm.

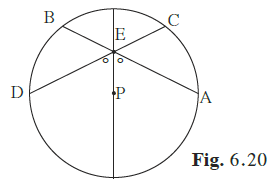
Construction: Draw perpendicular from point P to the chords CD and AB.

To prove: AB = CD

Proof: In ∆ MEP and ∆ NEP,

∠EMP = ∠ENP = 90°…………… (Given)

AEP = DEP

Thus, by AAS congruence rule, A MEP A NEP.

So, MP = NP…………………………(CPCT)

We know that chords equidistant from the centre are equal to each other.

Hence, AB = CD.

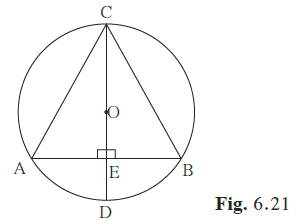
In ∆AEC and ∆BEC,

AE = BE…………(Perpendicular drawn from the centre of the circle to the chord bisects the chord)

CE = CE………….(Common)

∠ CEA = ∠ CEB = 90°

Thus, ∆AEC ≅ ∆BEC by SAS congruency

So, by CPCT, AC = CB

Thus, ∆ABC is an isosceles triangle.