Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 1 - Basic Concepts in Geometry

(i)

Co-ordinate of the point B is 2.

Co-ordinate of the point E is 5.

Since, 5 > 2

∴ d(B, E) = 5 - 2

∴ d(B, E) = 3

(ii)

Co-ordinate of the point J is -2.

Co-ordinate of the point A is 1.

Since, 1 > -2

∴ d(J, A) = 1 - (-2) = 1 + 2

∴ d(J, A) = 3

(iii) Co-ordinate of the point P is -4.

Co-ordinate of the point C is 3.

Since, 3 > -4

∴ d(P, C) = 3 - (-4) = 3 + 4

∴ d(P, C) = 7

(iv)

Co-ordinate of the point J is -2.

Co-ordinate of the point H is -1.

Since, -1 > -2

∴ d(J, H) = - 1 - (-2) = -1 + 2

∴ d(J, H) = 1

(v)

Co-ordinate of the point K is -3.

Co-ordinate of the point O is 0.

Since, 0 > -3

∴ d(K, O) = 0 - (-3) = 0 + 3

∴ d(K, O) = 3

(vi)

Co-ordinate of the point O is 0.

∴ Co-ordinate of the point E is 5.

Since, 5 > 0

∴ d(O, E) = 5 - 0

∴ d(O, E) = 5

(vii)

Co-ordinate of the point P is -4.

Co-ordinate of the point J is -2.

Since -2 > -4

∴ d(P, J) = -2 - (-4) = - 2+ 4

∴ d(P, J) = 2

(viii)

Co-ordinate of the point Q is -5.

Co-ordinate of the point B is 2.

Since, 2 > -5

∴ d(Q, B) = 2 - (-5) = 2 + 5

∴ d(Q, B) = 7

(i)

Co-ordinate of point A is x = 1.

Co-ordinate of point B is y = 7

Since, 7 > 1

∴ d(A, B) = 7 - 1

∴ d(A, B) = 6

(ii)

Co-ordinate of point A is x = 6.

Co-ordinate of point B is y = -2.

Since, 6 > -2

∴ d(A, B) = 6 - (-2) = 6 + 2

∴ d(A, B) = 8

(iii)

Co-ordinate of point A is x = -3.

Co-ordinate of point B is y = 7.

Since, 7 > -3

∴ d(A, B) = 7 - (-3) = 7 + 3

∴ d(A, B) = 10

(iv)

Co-ordinate of point A is x = -4.

Co-ordinate of point B is y = -5.

Since, -4 > -5

∴ d(A, B) = -4 - (-5) = -4 + 5

∴ d(A, B) = 1

(v)

Co-ordinate of point A is x = -3.

Co-ordinate of point B is y = -6.

Since, -3 > -6

∴ d(A, B) = -3 - (-6) = -3 + 6

∴ d(A, B) = 3

(vi)

Co-ordinate of point A is x = 4.

Co-ordinate of point B is y = -8.

Since, 4 > -8

∴ d(A, B) = 4 - (-8) = 4 + 8

∴d(A, B) = 12

(i)

Given: d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3

d(P, Q) = 10 … (I)

d(P, R) + d(Q, R) = 7 + 3 = 10 … (II)

∴ d(P, Q) = d(P, R) + d(Q, R) … [From (I) and (II)]

∴ Point R is between the points P and Q

i.e. P - R - Q or Q - R - P.

∴ Points P, R, Q are collinear.

(ii)

Given: d(R, S) = 8, d(S, T) = 6, d(R, T) = 4

d(R, S) = 8 … (I)

d(S, T) + d(R, T) = 6 + 4 = 10 … (II)

∴ d(R, S) ≠ d(S, T) + d(R, T) … [From (I) and (II)]

∴ The given points are not collinear.

(iii)

Given: d(A, B) = 16, d(C, A) = 9, d(B, C) = 7

d(A, B) = 16 … (I)

d(C, A) + d(B, C) = 9 + 7 = 16 … (II)

∴ d(A, B) = d(C, A) + d(B, C) … [From (I) and (II)]

∴ Point C is between the points A and B.

i.e. A - C - B or B - C - A.

∴ Points A, C, B are collinear

(iv)

Given: d(L, M) = 11, d(M, N) = 12, d(N, L) = 8

d(M, N) = 12 … (I)

d(L, M) + d(N, L) = 11 + 8 = 19 … (II)

∴ d(M, N) ≠ d(L, M) + d(N, L) … [From (I) and (II)]

∴ The given points are not collinear.

(v)

Given: d(X, Y) = 15, d(Y, Z) = 7, d(X, Z) = 8

d(X, Y) = 15 … (I)

d(X, Z) + d(Y, Z) = 8 + 7= 15 … (II)

∴ d(X, Y) = d(X, Z) + d(Y, Z) … [From (I) and (II)]

∴ Point Z is between the points X and Y

i.e. X - Z - Y or Y - Z - X.

∴ Points X, Z, Y are collinear.

(vi)

Given: d(D, E) = 5, d(E, F) = 8, d(D, F) = 6

d(E, F) = 8 … (I)

d(D, E) + d(D, F) = 5 + 6 = 11 … (II)

∴ d(E, F) ≠ d(D, E) + d(D, F) … [From (I) and (II)]

∴ The given points are not collinear.

Given: d(A, C) = 10, d(C, B) = 8

Case I: Points A, B, C are such that, A - B - C.

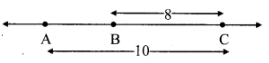
∴ d(A, C) = d(A, B) + d(B, C)

∴ 10 = d(A, B) + 8

∴ d(A, B) = 10 - 8

∴ d(A, B) = 2

Case II: Points A, B, C are such that, A - C - B.

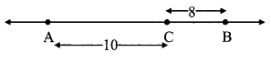
∴ d(A, B) = d(A, C) + d(C, B) = 10 + 8

∴ d(A, B) = 18

Case III: Points A, B, C are such that, B - A - C.

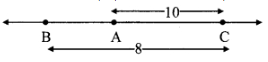
From the diagram,

d (A, C) > d(B, C)

Which is not possible

∴ Point A is not between B and C.

∴ d(A, B) = 2 or d(A, B) = 18.

Given: d(X, Y) = 17, d(Y, Z) = 8

Case I: Points X, Y, Z are such that, X - Y - Z.

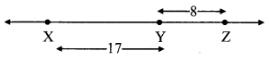
∴ d(X, Z) = d(X, Y) + d(Y, Z) = 17 + 8

∴ d(X, Z) = 25

Case II: Points X, Y, Z are such that, X - Z - Y.

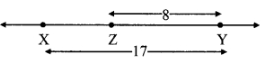
∴ d(X,Y) = d(X,Z) + d(Z,Y)

∴ 17 = d(X, Z) + 8

∴ d(X, Z) = 17 - 8

∴ d(X, Z) = 9

Case III: Points X, Y, Z are such that, Z - X - Y.

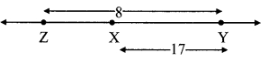
From the diagram,

d(X, Y) > d (Y, Z)

Which is not possible

∴ Point X is not between Z and Y.

∴ d(X, Z) = 25 or d(X, Z) = 9.

Given, l(AC) =11, l(BC) = 6.5

l(AC) = l(AB) + l(BC) … [A - B - C]

∴ 11= l(AB) + 6.5

∴ l(AB) = 11 - 6.5

∴ l(AB) = 4.5

ii. Given, l(ST) = 3.7, l(RS) = 2.5

l(RT) = l(RS) + l(ST) … [R - S - T]

= 2.5 + 3.7

∴ (RT) = 6.2

iii. l(XZ) =  

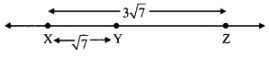
l(XZ) = l(X Y) + l(YZ) … [X - Y - Z]

∴ 3 √7 ⇒ √7 + l(YZ)

∴ l(YZ)= 3√7 - √7

∴ l(YZ) = 2 √7

Three non-collinear points form a triangle.

(i)

As per the table,

Co-ordinate of the point E is 9 and co-ordinate of the point D is -7.

Since, 9 > -7

∴ d(D, E) = 9 - (-7) = 9 + 7 = 16

∴ l(DE) = 16 … (I)

Also, co-ordinate of the point A is -3 and co-ordinate of the point B is 5.

Since, 5 > -3

∴ d(A, B) = 5 - (-3) = 5 + 3 = 8

∴ l(AB) = 8 … (II)

∴ l(DE) ≠ l(AB) … [From (I) and (II)]

∴ seg DE and seg AB are not congruent.

(ii)

As per the table,

Co-ordinate of the point B is 5 and co-ordinate of the point C is 2.

Since, 5 > 2

∴ d(B, C) = 5 - 2 = 3

∴ l(BC) = 3 … (I)

Also, co-ordinate of the point A is -3 and co-ordinate of the point D is -7.

Since, -3 > -7

∴ d(A, D) = -3 - (-7) = -3 + 7 = 4

∴ l(AD) = 4 ... (II)

∴ l(BC) ≠ l(AD) … [From (I) and (II)]

∴ seg BC and seg AD are not congruent.

(iii)

As per the table, co-ordinate of the point E is 9 and co-ordinate of the point B is 5.

Since, 9 > 5

∴ d(B, E) = 9 - 5 = 4

∴ l(BE) = 4 … (I)

Also, co-ordinate of the point A is -3 and co-ordinate of the point D is -7.

Since, -3 > -7

∴ d(A, D) = -3 - (-7) = 4

∴ l(AD) = 4 … (II)

∴ l(BE) =l(AD) … [From (I) and (II)]

∴ seg BE and seg AD are congruent.

Point M is the midpoint of seg AB…(Given)

∴ Length of AM is 4.

Since, point P is the midpoint of seg CD … (Given)

∴ l(CD) = 2 × l(CP)

∴ l(CD) = 2 × 2.5

∴ l(CD) = 5

Given: l(AB) = 5 cm, l(BP) = 2 cm, l(AP) = 3.4 cm

Since, 2 < 3.4 < 5

∴ l(BP) < l(AP) < l(AB)

∴ seg BP < seg AP < seg AB

(i) Ray RS or ray RT

(ii) Ray PQ

(iii) Line QR

(iv) Ray QR, ray QS, ray QT, ray RQ, ray SQ, ray TQ

(v) Ray RP and ray RS, ray RQ and ray RT

(vi) Ray ST, ray SR

(vii) Point S

(i)

Points equidistant from point B are:

A and C, because d(B, A) = d(B, C) = 2

P and D, because d(B, P) = d(B, D) = 4

(ii)

Points equidistant from point Q are:

L and U, because d(Q, L) = d(Q, U) = 1

P and R, because d(P, Q) = d(Q, R) = 2

(iii)

(a)

Co-ordinate of the point U is -5 and of the point V is 5.

Since, 5 > -5

∴ d(U, V) = 5 - (-5) = 5 + 5

∴ d(U, V) = 10

(b)

Co-ordinate of the point P is -2 and co-ordinate of the point C is 4.

Since, 4 > -2

∴ d(P, C) = 4 - (-2) = 4 + 2

∴ d(P, C) = 6

(c)

Co-ordinate of the point V is 5 and co-ordinate of the point B is 2.

Since, 5 > 2

∴ d(V, B) = 5 - 2

∴ d(V, B) = 3

(d)

Co-ordinate of the point U is -5 and co-ordinate of the point L is -3.

Since, -3 > -5

∴ d(U, L) = -3 - (-5) = -3 + 5

∴ d(U, L) = 2

(i)

If a quadrilateral is a parallelogram, then its opposite angles are congruent.

(ii)

If a quadrilateral is a rectangle, then its diagonals are congruent.

(iii)

If a triangle is isosceles triangle, then the segment joining the vertex of a triangle and midpoint of the base is perpendicular to the base.

(i)

If the alternate angles made by two lines and their transversals are congruent, then the two lines are parallel.

(ii)

If two parallel lines are intersected by a transversal, then the interior angles formed by the transversal are supplementary.

(iii)

If the diagonals of a quadrilateral are congruent, then that quadrilateral is a rectangle.

(A)

A segment have only one midpoint.

When two distinct lines intersect, they have only one intersection point.

(C)

When the three points are non-collinear, three lines can be determined with these points.

When the three points are collinear, only one line can be determined joining these points.

So, one or three lines can be determined.

Coordinate of point A is -2 and coordinate of point B is 5.

Since, 5 > -2

∴ d(A, B) = 5 - (-2) = 5 + 2 = 7

Since, P - Q - R

∴ d(P, R) = d(P, Q) + d(Q, R)

∴ 10 = 2 + d(Q, R)

∴ d(Q, R) = 8

Co-ordinate of the point P is 3 co-ordinate of the point Q is -5.

Since, 3 > -5

d(P, Q) = 3 - (-5) = 3 + 5

∴ d(P, Q) = 8

Co-ordinate of the point Q is -5 and co-ordinate of the point R is 6.

Since, 6 > -5

d(Q, R) = 6 - (-5) = 6 + 5

∴ d(Q, R) = 11

Co-ordinate of the point P is 3 and co-ordinate of the point R is 6.

Since, 6 > 3

d(P, R) = 6 - 3

∴ d(P, R) = 3

(i)

d(P, Q) + d(Q, R) = 8 + 11 = 19 … (I)

d(P, R) = 3 … (II)

∴ d(P, Q) + d(Q, R) ≠ d(P, R) … [From (I) and (II)]

∴ The given statement is false.

(ii)

d(P, R) + d(R, Q) = 3 + 11 = 14 … (I)

d(P,Q) = 8 … (II)

∴ d(P, R) + d(R, Q) ≠ d(P, Q) … [From (I) and (II)]

∴ The given statement is false.

(iii)

d(R, P) + d(P, Q) = 3 + 8 = 11 … (I)

d(R, Q) = 11 … (II)

∴ d(R,P) + d(P,Q) = d(R,Q) … [From (I) and (II)]

∴ The given statement is true.

(iv)

d(P, Q) - d(P, R) = 8 - 3 = 5 … (I)

d(Q,R) = 11 … (II)

∴ d(P, Q) - d(P, R) ≠ d(Q, R) … [From (I) and (II)]

∴ The given statement is false.

(i)

Co-ordinate of first point is 3 and co-ordinate of second point is 6.

Since, 6 > 3

∴ Distance between the points = 6 - 3 = 3

(ii)

Co-ordinate of first point is -9 and Co-ordinate of second point is -1.

Since, -1 > -9

∴ Distance between the points = -1 - (-9) = -1+9 = 8

(iii)

Co-ordinate of first point is -4 and co-ordinate of second point is 5.

Since, 5 > -4

∴ Distance between the points = 5 - (-4) = 5 + 4 = 9

(iv)

Co-ordinate of first point is 0 and co-ordinate of second point is -2.

Since, 0 > - 2

∴ Distance between the points = 0 - (-2) = 0 + 2 = 2

(v)

Co-ordinate of first point is x + 3 and co-ordinate of second point is x - 3.

Since, x + 3 > x - 3

∴ Distance between the points = x + 3 - (x - 3) = x + 3 - x + 3 = 3 + 3 = 6

(vi)

Co-ordinate of first point is -25 and co-ordinate of second point is -47.

Since, -25 > -47

∴ Distance between the points = -25 - (-47) = -25 + 47 = 22

(vii)

Co-ordinate of first point is 80 and co-ordinate of second point is -85.

Since, 80 > -85

∴ Distance between the points = 80 - (-85) = 80 + 85 = 165

Let point Q be at a distance of 8 units from P and on left side of P

Let point R be at a distance of 8 units from P and on right side of P.

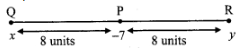
(i)

Let the co-ordinate of point Q be x.

Co-ordinate of point P is -7.

Since, point Q is to the left of point P.

∴ -7 > x

∴ d(P, Q) = -7 - x

∴ 8 = -7 - x

∴ x = - 7 - 8

∴ x = -15

(ii)

Let the co-ordinate of point R be y.

Co-ordinate of point P is -7.

Since, point R is to the right of point P.

∴ y > -7

∴ d(P, R) = y - (-7)

∴ 8 = y + 7

∴ 8 - 7 = y

∴ y = 1

∴ The co-ordinates of the points at a distance of 8 units from P are -15 and 1.

(i)

Given: d(A, C) = 17, d(B, C) = 6.5

d(A, C) = d(A, B) + d(B, C) … [A - B - C]

∴ 17 = d(A, B) + 6.5

∴ d(A, B)= 17 - 6.5

∴ d(A, B) = 10.5

(ii)

Given: d(P, Q) = 3.4, d(Q, R) = 5.7

d(P, R) = d(P, Q) + d(Q, R) …[P - Q - R]

= 3.4 + 5.7

∴ d(P, R) = 9.1

Let point B be at a distance of 7 units from A and on left side of A.

Let point C be at a distance of 7 units from A and on right side of A.

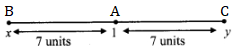
i. Let the co-ordinate of point B be x.

Co-ordinate of point A is 1.

Since, point B is to the left of point A.

∴ 1 > x

∴ d(A, B) = 1 - x

∴ 7 = 1 - x

∴x = 1 - 7

∴ x = -6

ii. Let the co-ordinate of point C be y.

Co-ordinate of point A is 1.

Since, point C is to the right of point A.

∴ y > 1

∴ d(A, C) = 7 - 1

∴ 7 = y - 1

∴ 7 + 1 = y

∴ y = 8

∴ The co-ordinates of the points at a distance of 7 units from A are -6 and 8.

(i) If a quadrilateral is a rhombus, then it is a square.

(ii) If two angles are in a linear pair, then they are supplementary.

(iii) If a figure is a triangle, then it is formed by three segments.

(iv) If a number has only two divisors, then it is a prime number.

(i) If a figure is a triangle, then the sum of the measures of its angles is 180°.

(ii) If two angles are complement of each other, then sum of their measures is 90°.

(iii) If two lines are parallel, then the corresponding angles formed by a transversal of two lines are congruent.

(iv) If a number is divisible by 3, then the sum of its digits is also divisible by 3.

(i)

Antecedent (Given): All the sides of the triangle are congruent.

Consequent (To prove): All the angles are congruent.

(ii)

Conditional statement: "If a quadrilateral is a parallelogram then its diagonals bisect each other.

Antecedent (Given): Quadrilateral is a parallelogram.

Consequent (To prove): Its diagonals bisect each other.

(i)

Conditional statement: "If two triangles are equilateral, then they are similar.

Antecedent (Given): Two triangles are equilateral.

i.e. ∆ABC and ∆PQR are equilateral triangle.

Consequent (To prove): Triangles are similar

i.e. ∆ABC ∼ ∆PQR

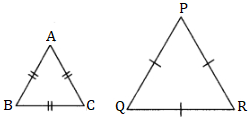
(ii)

Antecedent (Given): Angles in a linear pair are congruent.

∠CDA and ∠CDB are angles in a linear pair i.e. ∠CDA = ∠CDB

Consequent (To prove): Each angle is a right angle.

i.e. ∠CDA = ∠CDB = 90°

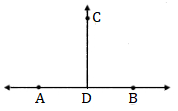
(iii)

Antecedent (Given): Altitude drawn on two sides of a triangle are congruent.

i.e. In ∆ABC, AD ⊥ BC. and BE ⊥ AC, seg AD ≅ seg BE

Consequent (To prove): Two sides are congruent.

i.e. side BC ≅ side AC