Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 1 - Sets
Sets Exercise 1.1
Solution 1
X = {2, 4, 6, 8, 10, 12, …}
Y = {2}
Z = {…., -4, -3, -2, -1}
T = {sa, re, ga, ma, pa, dha, ni}
Solution 2
![]() is
an element of the set Q
is
an element of the set Q
-2 is not an element of set N
Set P is a set of all p's such that p is an odd number
Solution 3
1.Listing method:
A ={ S, U, N, D, A, Y }
Rule method:
A ={ y|y is a letter in the word 'SUNDAY' }
2.Listing method:
B ={ 1, 2, 3, 4, 5,… }
Rule method:
B ={ y|y ![]() N}
N}
Solution 4
(i) X ={Chaitra, Vaishakha, Jyestha, Aashadha, Sharavana, Bhadrapada, Ashiwina, Karthika, Margashirsha, Pausha, Magha, Falguna}
(ii) B = {C, O, M, P, L, E, N, T}
(iii) C = {Nose, Ears, Eyes, Tongue, Skin}
(iv) D = {2, 3, 5, 7, 11, 13, 17, 19}
(v) E = {Asia, Africa, North America, South America, Antarctica, Europe, Australia}
Solution 5
(i) A = {x | x = n2, n ![]() N, n
N, n ![]() 10 }
10 }
(ii) B = {x | x = 6n, n ![]() N, n < 9 }
N, n < 9 }
(iii) C = {y | y is a letter in the word 'SMILE' }
(iv) D = {y | y is a day of the week }
(v) E = {y | y is a letter in the word 'ate' }
Sets Exercise 1.2
Solution 1
A = {x | 3x - 1 = 2}
3x - 1 = 2
![]() 3x = 2 + 1
3x = 2 + 1
![]() x = 1
x = 1
B = {x | x is a natural number but x is neither prime nor composite}
1 is the only number which satisfies the given condition
C = {x | x ![]() N, x < 2}
N, x < 2}
1 is the only natural number less than 2.
![]() x = 1
x = 1
So A, B and C are equal sets
Solution 2
A = {2}, because 2 is the only even prime number.
B = {x | 7x - 1 = 13},
7x - 1 = 13
![]() 7x = 13 +1
7x = 13 +1
![]() 7x = 14
7x = 14
![]() x = 2
x = 2
So A and B are equal sets.
Solution 3
(i) A = {a | a is a natural number smaller than zero}
There is no such natural number, which is less than 0.
![]() A is an empty set
A is an empty set
(ii) B = {x | x2 = 0}
![]() x = 0, Set B has element 0,
so it is not empty
x = 0, Set B has element 0,
so it is not empty
(iii) C = {x | 5x -
2 = 0, x ![]() N}
N}
![]() 5x = 2 , x = 2/5
But given that x
5x = 2 , x = 2/5
But given that x ![]() N, 2/5
N, 2/5 ![]() N
N
![]() Set C is an empty set
Set C is an empty set
Solution 4
(i) A = {1, 2, 3,…, 8, 9 }
∴ Set A is finite
(ii) B = {…, -4, -3, -2}
∴ Set B is infinite
(iii) Number of students in class 9 is countable
∴ Set is finite
(iv) Number of people in a village is countable
∴ Set is finite
(v) Number of apparatus in a laboratory is countable
∴ Set is finite
(vi) Set of whole numbers is infinite set, because you can go on writing whole numbers
(vii) Set of rational number is infinite set, because you can go on writing rational numbers
Sets Exercise 1.3
Solution 1
(i) C ![]() B, False because all elements of Set C are not present in Set B
B, False because all elements of Set C are not present in Set B
(ii) A ![]() D, False because all elements of Set A are not present in Set D
D, False because all elements of Set A are not present in Set D
(iii) D ![]() B, False because all elements of Set D are not present in Set B
B, False because all elements of Set D are not present in Set B
(iv) D ![]() A, True because all elements of Set D are present in Set A
A, True because all elements of Set D are present in Set A
(v) B ![]() A, False because all elements of Set B are not present in Set A
A, False because all elements of Set B are not present in Set A
(vi) C ![]() A, True because all elements of Set C are present in Set A
A, True because all elements of Set C are present in Set A
Solution 2
(i)
U = {1, 2, 3, …, 18, 19, 20}
X = {8, 9, 10, 11, 12, 13, 14}
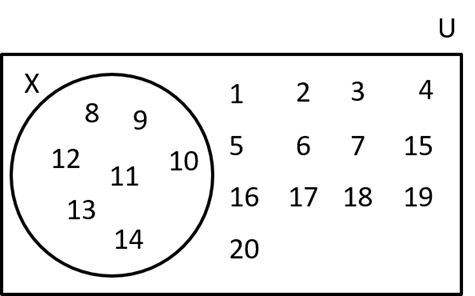
(ii)
Y = {2, 3, 5, 7, 11, 13, 17, 19}
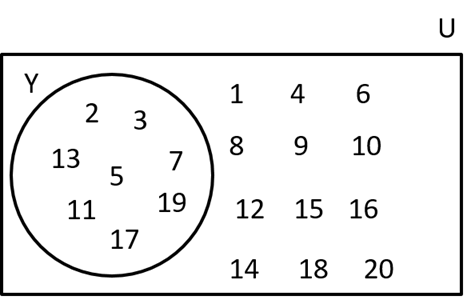
Solution 3
(i)

(ii)
U = {1, 2, 3, 7, 8, 9, 10, 11, 12}
P' = {2, 8, 9, 11, 12}
![]() (P')' = U
(P')' = U ![]() P = {1, 3, 7, 10}
P = {1, 3, 7, 10}
P = {1, 3, 7, 10} … (Given)
So,
(P')' = P
Solution 4
The subsets of set A are as follows:
ɸ, {1}, {3}, {2}, {7}, {1,3}, {1,2}, {1,7}, {3,2}, {3,7}, {2,7}, {1,3,2}, {1,3,7}, {1,2,7}, {3,2,7}, {1,3,2,7}.
Solution 5
(i)
a) Residents of Pune are also residents of Maharashtra
P ![]() H
H
b) Residents of Madhya Pradesh are also residents of India
M ![]() B
B
c) Residents of Indore are also residents of Madhya Pradesh
I ![]() M
M
d) Residents of Maharashtra are also residents of India
H ![]() B
B
(ii)
We can say that, the given sets P, M, I, H are all sub sets of B
∴B can be chosen as the Universal Set.
Solution 6
(i)
A = {5, 10, 15, …}
B = {7, 14, 21, …}
C = {12, 24, 36, …}
We can say sets A, B and C are subsets of Natural numbers, Whole numbers or Integers
N = {1, 2, 3, …}
W = {0, 1, 2, 3, …}
I = {…, -2, -1, 0, 1, 2, …}
(ii)
P = {4, 8, 12, …}
T = {4, 16, 36, …}
We can say sets P and T are subsets of Natural numbers, Whole numbers or Integers
N = {1, 2, 3, …}
W = {0, 1, 2, 3, …}
I = {…, -2, -1, 0, 1, 2, …}
Solution 7
The complement of set A is the set of students who secure less than 50% marks in Maths.
Sets Exercise 1.4
Solution 1
Given: n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7
Now, n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
∴ 29 = 15 + n(B) - 7
∴ 29 - 15 + 7 = n(B)
∴ n(B) = 21
Solution 2
Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.
∴ n(U) = 125, n(T) = 80, n(C) = 60,
∴ number of students who drink Tea and Coffee = n(T ∩ C) = 20
Now,
n(T ∪ C) = n(T) + n(C) - n(T ∩ C)
= 80 + 60 - 20
∴ n(T ∪ C) = 120
∴ 120 students drink tea or coffee
Since, there are 125 students in the hostel.
Number of students who do not drink tea or coffee = n(U) - n(T ∪ C)
= 125 - 120
= 5
∴ 5 students do not drink tea or coffee.
Solution 3
Let U be the set of students who appeared for the exam
E be the set of students who passed in English
M be the set of students who passed in Maths
∴ n(E) = 50, n(M) = 60
Since, 40 students passed in both the subjects.
∴ n(M ∩ E) = 40
Since, none of the students failed in both subjects
∴ Total students = n(E ∪ M)
= n(E) + n(M) - n(E ∩ M)
= 50 + 60 - 40
= 70
∴ The number of students who passed at least in one of the subjects is 70.
Solution 4
Let U be the set of students of class IX
R be the set of students who follow the hobby of rock climbing
S be the set of students who follow the hobby of sky watching
∴ n(U) = 220, n(R) = 130, n(S) = 180
Since, 110 students follow both the hobbies.
∴ n(R ∩ S) = 110
Now, n(R ∪ S) = n(R) + n(S) - n(R ∩ S)
∴ n(R ∪ S) = 130 + 180 - 110
∴ n(R ∪ S) = 200
∴ 200 students follow the hobby of rock climbing or sky watching.
Also, total number of students = 220.
Number of students who do not follow the hobby of rock climbing or sky watching
= n(U) - n(R ∪ S)
= 220 - 200
= 20
Number of students who follow the hobby of rock climbing only
= n(R) - n(R ∩ S)
= 130 - 110
= 20
Number of students who follow the hobby of sky watching only
= n(S) - n(R ∩ S)
= 180 - 110
= 70
Solution 5
(i) A = {x, y, z, m, n}
(ii) B = {p, q, r, m, n}
(iii) A ∪ B = {x, y, z, m, n, p, q, r }
(iv) U = {x, y, z, m, n, p, q, r, s, t}
(v) A' = {p, q, r, s, t}
(vi) B' = {x, y, z, s, t}
(vii) (A ∪ B )' = {s, t}
Sets Exercise Problem set 1
Solution 1
(i)
M![]() N = { } = Φ
N = { } = Φ
(ii)
P = {x | x is an odd natural number, 1 < x ≤ 5}
∴ P = {3, 5}
(iii)
P = {1, 2, ........., 10}
P is a finite set.
(iv)
M![]() N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4}
N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4}
∴ N = {3, 4, 5, 6}
(v)
Since, P ⊆ M
∴ P ![]() = M
= M
∴ P ![]() (P
(P![]() M) = P
M) = P
(vi)
Since the parallel lines does not intersect.
∴ It is an empty set.
Solution 2
(i) Colours of the rainbow is a set.
(ii)
N = {1, 2, 3, 4, …} and W = {0, 1, 2, 3, 4, …}
∴ N ![]() W = {1, 2, 3, 4, …}
W = {1, 2, 3, 4, …}
(iii)
P = {x | x is a letter of the word 'indian'}
∴ P = {i, n, d, a, n}
(iv) T ![]() M = {1, 2, 3, 4, 5, 7, 8}
M = {1, 2, 3, 4, 5, 7, 8}
Solution 3
Let U be the set of all the persons
E be the set of persons who speak English and
F be the set of persons who speak French.
∴ n(E) = 72, n(F) = 43
Since, each one out of 100 persons speak at least one language.
∴ n(U) = n(E ∪ F)= 100
Now, n(E ∪ F) = n(E) + n(F) - n(E ∩ F)
∴ 100 = 72 + 43 - n(E ∩ F)
∴ n(E ∩ F) = 72 + 43 - 100
∴ n(E ∩ F) = 15
∴ Number of people who speak English and French = 15
Number of people who speak only English = n(E) - n(E ∩ F)
= 72 - 15 = 57
Number of people who speak only French = n(F) - n(E ∩ F)
= 43 - 15 = 28
Solution 4
Let A be the trees planted by Parth and B be the trees planted by Pradnya
∴ n(A) = 70 and n(B) = 90
Total number of trees planted by Parth and Pradnya = n(A ∩ B) = 25
Number of trees planted by Parth or Pradnya = n(A ∪ B)
= n(A) + n(B) - n(A ∩ B)
= 70 + 90 - 25 = 135
∴ Total of 135 trees were planted by Parth or Pradnya.
Solution 5
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
∴ 36 = 20 + 28 - n(A ∩ B)
∴ n(A ∩ B) = 20 + 28 - 36
∴ n(A ∩ B) = 12
Solution 6
Let U be the set of all the students
∴ n(U) = 28
Let D be the set of students who have dog as pet and C be the set of students who have cat as pet.
Since, 10 students have dog and cat as their pet animal
∴ n(D ∩ C) = 10
Number of students who have cat or dog as pet
= n(D ∪ C)
= 8 + 10 + 6
= 24
Number of students who do not have dog or cat as pet = n (U) - n(D ∪ C)
= 28 - 24
= 4
Solution 7
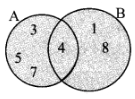
(i) A = {3, 4, 5, 7}, B = {1, 4, 8}
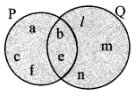
(ii) P = {a, b, c, e, f}, Q = {l, m, n , e, b}
(iii)
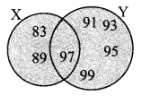
X = {x | x is a prime number between 80 and 100} i.e. X = {83, 89, 97}
Y = {y | y is an odd number between 90 and 100 }
i.e. Y = {91, 93, 95, 97, 99}
Solution 8
Rhombus, square, parallelogram and rectangle all are quadrilaterals.
∴ Y ⊆ X, S ⊆ X, T ⊆ X, V ⊆ X
Every square is a rhombus, parallelogram and rectangle.
∴ S ⊆ Y, S ⊆ T, S ⊆ V
Every rhombus and rectangle is a parallelogram.
∴ Y ⊆ T, V ⊆ T
Solution 9
Let M = {2, 3, 4, 8} and ϕ = { }
∴ M ∪ ϕ = {2, 3, 4, 8}
∴ M ∪ ϕ = M
Also, M ∩ ϕ = { }
∴ M ∩ ϕ = { }
Solution 10
U = {1,2, 3,4, 5, 7, 8, 9, 10, 11, 13}
A = {1, 2, 3, 5, 7}
B = {1, 5, 8, 9, 10}
A ∪ B = {1, 2, 3, 5, 7, 8, 9, 10}
A ∩ B = {1, 5}
Solution 11
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
= 7 + 13 - 4
= 16
∴ n(A ∪ B) = 16

