Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 2 - Real Numbers
Real Numbers Exercise 2.1
Solution 1(i)
Here, denominator = 5 = 1 × 5
Since, 5 is the only prime factor in the denominator.
∴
The decimal form of the rational number 
will
be of terminating type.
Solution 1(ii)
Here, denominator = 11 = 1 × 11
Since, the denominator has prime factors other than 2 or 5 in the prime factorization.
∴ The decimal form of the
rational number 
will be of
non-terminating recurring type.
Solution 1(iii)
Here, denominator = 16 = 24
Since, 2 is the only prime factor in the prime factorization of denominator.
∴ The decimal form of the
rational number 
will be of terminating
type.
Solution 1(iv)
Here, denominator = 125 = 53
Since, 5 is the only prime factor in the prime factorization of denominator.
∴
The decimal form of the rational number 
will be of terminating
type.
Solution 1(v)
Here, denominator = 6 = 2 × 3
Since, the denominator have prime factors other than 2 or 5 in the prime factorization.
∴ The decimal form of the
rational number 
will be of non-terminating
recurring type.
Solution 2(i)
Solution 2(ii)
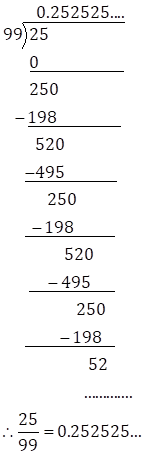
Solution 2(iii)
Solution 2(iv)
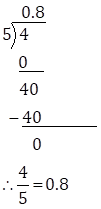
Solution 2(v)
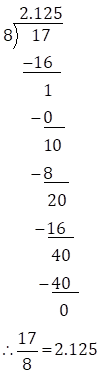
Solution 3(i)
Let x=0.6… (I)
∴ x = 0.666…
Since, only one digit which is 6 is repeating after the decimal point.
Thus, multiplying both sides by 10, we get
10x = 6.666…
(II)
Subtracting (I) from (II), we get
Solution 3(ii)
Let 
… (I)
∴ x = 0.3737…
Since, two numbers i.e. 3 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100, we get
100x = 37.3737……
… (II)
Subtracting (I) from (II), we get
Solution 3(iii)
Let 
… (I)
∴ x = 3.1717…
Since, two numbers i.e. 1 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100, we get
100x = 317.1717…
… (II)
Subtracting (I) from (II)
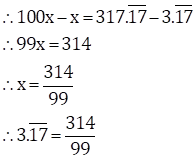
Solution 3(iv)
Let 
… (I)
∴ x = 15.898989…
Since, two numbers i.e. 8 and 9 are repeating after the decimal point.
Thus, multiplying both sides by 100, we get
100x = 1589.8989…
… (II)
Subtracting (I) from (II)
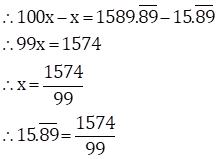
Solution 3(v)
Let 
… (I)
∴ x = 2.514514…
Since, three numbers i.e. 5, 1 and 4 are repeating after the decimal point.
Thus, multiplying both sides by 1000, we get
1000x = 2514.514514…
… (II)
Subtracting (I) from (II)
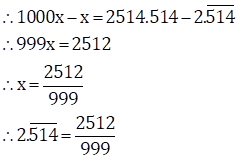
Real Numbers Exercise 2.2
Solution 1
Let us assume that 
is
not an irrational number.
As is rational,
we can find co-prime integers 'p' and 'q' (q ≠ 0) such that
Since, p and q are
integers, 
is a rational number.
is a rational
number, which is a contradiction.
Thus, is
an irrational number.
Solution 2
Let us assume that 
is
not an irrational number.
As is rational,
we can find co-prime integers 'p' and 'q' (q ≠ 0) such that
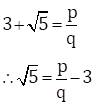
Since, p and q are
integers, 
is a rational number.
is a rational
number, which is a contradiction.
Thus, is
an irrational number.
Solution 3
(i)
Draw a number line and take points O at 0 and A at 2.
Draw AB perpendicular to the number line such that AB = 1 unit.
Now, in ∆OAB, m∠OAB = 90°
By Pythagoras theorem, we have
(OB)2 = (OA)2 + (AB)2
= (2)2 + (1)2
= 4 + 1
∴ (OB)2 = 5
Taking square root on both the sides, we get
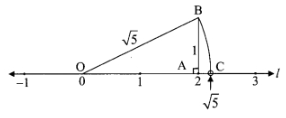
With O as centre and radius equal to OB, draw an arc to intersect the number line at C.
The coordinate of
point C is 
(ii)
Draw a number line and take points O at 0 and X at 2.
Draw XY perpendicular to the number line such that XY = 1 unit.
Now, in ∆OXY, m∠OXY = 90°
By Pythagoras theorem, we have
(OY)2 = (OX)2 + (XY)2
= (3)2 + (1)2
= 9 + 1
∴ (OY)2 = 10
Taking square root on both the sides, we get
With O as centre and radius equal to OY, draw an arc to intersect the number line at Z.
The coordinate of
point Z is 
Solution 4
(i)
0.3 = 0.30 and -0.5 = -0.50
We know that,
0. 30 > 0.29 >….. > 0.20>... > -0.20>…. > -0.30>…> -0.50
∴ The three rational numbers between 0.3 and -0.5 are -0.3, -0.2 and 0.2.
(ii)
-2.3 = -2.30 and -2.33 = -2.330
We know that,
-2.30 > -2.301 > … > -2.310 >….. > -2.320 > -2.321 >…> -2.33
∴ The three rational numbers between -2.3 and -2.33 are -2.301, -2.310 and -2.320.
(iii)
5.2 = 5.20 and 5.3 = 5.30
We know that,
5.30 > 5.29 > … > 5.22 > 5.21 > 5.20
∴ The three rational numbers between 5.2 and 5.3 are 5.21, 5.22 and 5.29.
(iv)
-4.5 = -4.50 and -4.6 = -4.60 We know that,
-4.50 > -4.51 > -4.52 >… > - 4.55 >…> -4.59 > -4.60
∴ The three rational numbers between -4.5 and -4.6 are -4.51, -4.52 and -4.59.
Real Numbers Exercise 2.3
Solution 1
(i)
Order of the surd 
is 3.
(ii)
Order of the surd 
is 2.
(iii)
Order of the surd 
is 4.
(iv)
Order of the surd 
is 2.
(v)
Order of the surd 
is 3.
Solution 2
(i) 
Here a = 51, order of surd n = 3
But 3rd root of 51 is not a rational number.
∴ is an irrational number.
∴ is a surd.
(ii) 
Here, a = 16, n = 4
2 is not an irrational number.
∴ is not a surd.
(iii) 
Here a = 81, order of surd n = 5
But 5th root of 81 is not a rational number
∴ is an irrational number.
Thus, is a surd.
(iv) 
Here, a = 256, n = 2
16 is not an irrational number.
∴ is not a surd.
(v) 
Here, a = 64, n = 3
4 is not an irrational number.
∴ is not a surd.
(vi) 
Here, 
and n = 2
is a positive rational number 2 is a positive integer greater than 1.
Thus, is a surd.
Solution 3
(i) 
For 
order is same and radicands are equal.
Thus, 
are like surds.
(ii) 
For 
order is same but radicands are not equal.
Thus, 
are unlike surds.
(iii) 
For 
order is same and radicands are equal.
Thus, 
are like surds.
(iv) 
For 
order is same and radicands are equal.
Thus, 
are like surds.
(v) 
For 
order is same but radicands are not equal.
Thus, 
are unlike surds.
(vi) 
For 
order is same but the radicands are not equal.
Thus, 
are unlike surds.
Solution 4
(i)
(ii)
(iii)
(iv)
(v)
Solution 5
(i) 
Since, 98 > 75
(ii) 
Since, 247 < 274
(iii) 
Since, 28 > 28
(iv) 
Since, 125 > 98
(v) 
Since, 672 > 162
(vi) 
Since, 75 < 81
(vii) 
Since, 49 > 20
Solution 6
(i)
(ii)
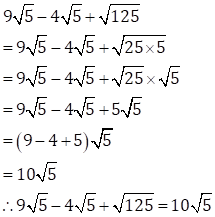
(iii)
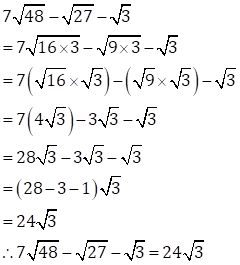
(iv)
Solution 7
(i)
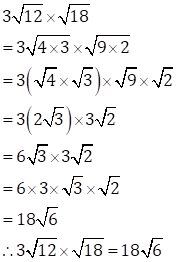
(ii)
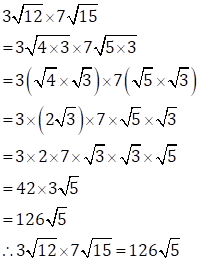
(iii)
(iv)
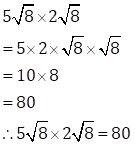
Solution 8
(i)
(ii)
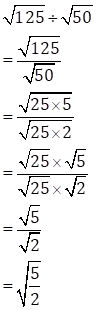
(iii)
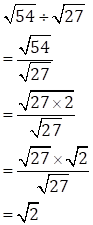
(iv)
Solution 9(i)
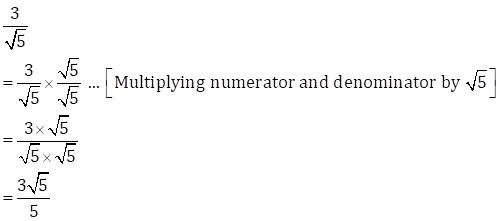
Solution 9(ii)
Solution 9(iii)
Solution 9(iv)
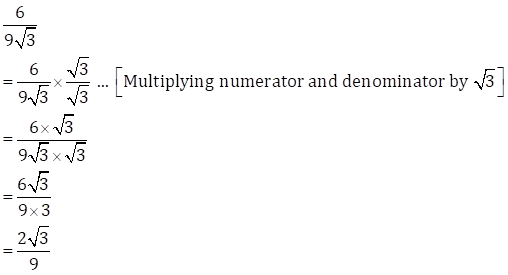
Solution 9(v)
Real Numbers Exercise 2.4
Solution 1(i)
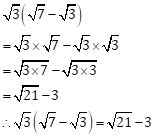
Solution 1(ii)
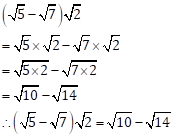
Solution 1(iii)
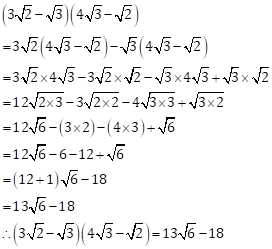
Solution 2(i)
Solution 2(ii)
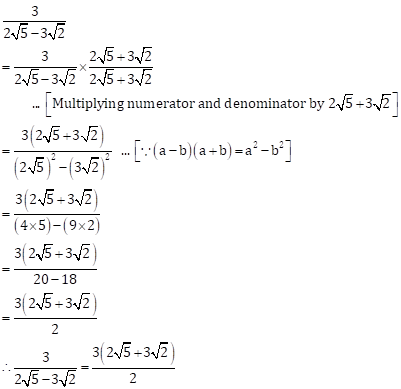
Solution 2(iii)
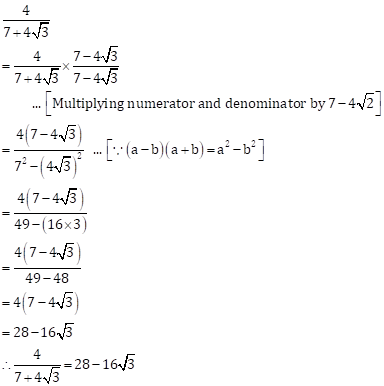
Solution 2(iv)
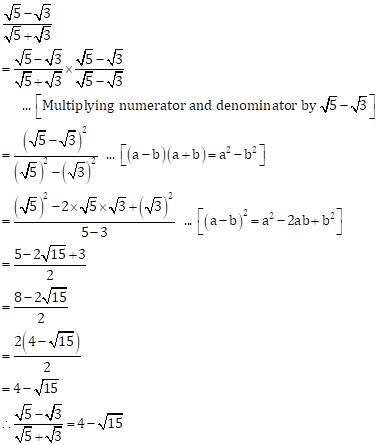
Real Numbers Exercise 2.5
Solution 1(i)
|15 - 2| = |13| = 13
Solution 1(ii)
|4 - 9| = |-5| = 5
Solution 1(iii)
|7| × |-4| = 7 × 4 = 28
Solution 2(i)
|3x - 5| = 1
∴ 3x - 5 = 1 or 3x - 5 = -1
∴ 3x = 1 + 5 or 3x = -1 + 5
∴ 3x = 6 or 3x = 4
Solution 2(ii)
|7 - 2x| = 5
∴ 7 - 2x = 5 or 7 - 2x = -5
∴ 7 - 5 = 2x or 7 + 5 = 2x
∴ 2x = 2 or 2x = 12
Solution 2(iii)
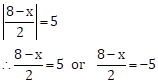
Multiplying both the sides by 2
∴ 8 - x = 10 or 8 - x = -10
∴ 8 - 10 = x or 8 + 10 = x
∴ x = -2 or x = 18
Solution 2(iv)
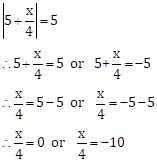
Multiplying both the sides by 4
∴ x = 0 or x = -40
Real Numbers Exercise Problem set 2
Solution 1(i)
(B)
which
is rational
is
a rational number
which
is rational
Cannot
be reduced as a rational number.
So, is
an irrational number.
Solution 1(ii)
(D)
0.17 is terminating and so it a rational number.
is
non-terminating but repeating and so it a rational number.
is
non-terminating but repeating and so it a rational number.
0.101001000… is non-terminating non-repeating decimal number and hence it is an irrational number.
Solution 1(iii)
(C)
For 
denominator
= 5 = 1 × 5
Therefore, its decimal expansion is terminating.
For 
denominator
= 16 = 24
Therefore, its decimal expansion is terminating.
For 
denominator
= 11 = 1 × 11
Since, the denominator has prime factors other than 2 or 5 in the prime factorization.
Therefore, its decimal expansion is non-terminating.
For 
denominator
= 25 = 52
Therefore, its decimal expansion is terminating.
Solution 1(iv)
(D)
Every point on the number line represent real numbers.
Solution 1(v)
(A)
Let 
…
(I)
i.e. x = 0.44444….
Since, e number 4 is repeating after decimal point.
So, multiplying above equation by 10
∴ 10x = 4.44444…
… (II)
Subtracting (I) from (II), we get
∴ 9x = 4
Solution 1(vi)
(C)
If n is not a
perfect square, 
is
an irrational number.
Solution 1(vii)
(C)
which
is a rational number
Thus, 
is
not a surd.
Solution 1(viii)
(C)
Thus, the order of
the surd 
is
6.
Solution 1(ix)
(A)
Conjugate pair of 
is
Solution 1(x)
(B)
Solution 2
(i)
(ii)
Let x = 
…
(I)
i.e. x = 29.568568….
Since, three numbers i.e. 5, 6 and 8 are repeating after the decimal point.
So, multiplying both sides by 1000, we get
1000x = 29568.568568…
… (II)
Subtracting (I) from (II), we get
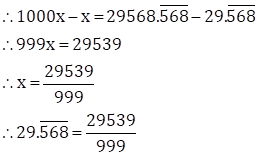
(iii)
Since, three numbers i.e. 3, 1 and 5 are repeating after the decimal point.
So, multiplying both sides by 1000, we get
1000x = 9315.315315…
… (II)
Subtracting (I) from (II), we get
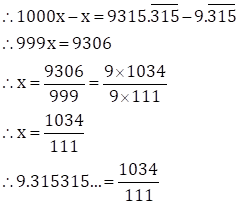
(iv)
Since, three numbers i.e. 4, 1 and 7 are repeating after the decimal point.
So, multiplying both sides by 1000, we get
1000x = 357417.417417…
… (II)
Subtracting (I) from (II), we get
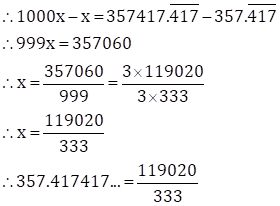
(v)
i.e. x = 30.219219…
Since, three numbers i.e. 2, 1 and 9 are repeating after the decimal point.
So, multiplying both sides by 1000, we get
1000x = 30219.219219…
… (II)
Subtracting (I) from (II), we get
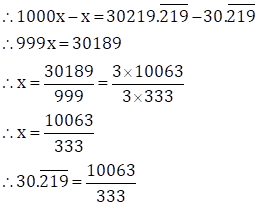
Solution 3
(i)
(ii)
(iii)
(iv)
(v)
Solution 4
Let us assume that 
is
not an irrational number.
As is
rational, we can find co-prime integers 'p' and 'q' (q ≠ 0) such that
Since, p and q are
integers, 
is a rational
number.
is a
rational number, which is a contradiction.
Thus, is
an irrational number.
Solution 5
(i)
(ii)
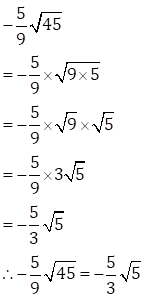
Solution 6
(i)
Now, 
which
is a rational number.
is the
simplest form of the rationalizing factor of 
(ii)
Now, 
which
is a rational number.
is the
simplest form of the rationalizing factor of 
(iii)
Now, 
which
is a rational number.
is the
simplest form of the rationalizing factor of 
(iv)
Now, 6 is a rational number.
is the
simplest form of the rationalizing factor of 
(v)
Now, 
which
is a rational number.
is the
simplest form of the rationalizing factor of 
(vi)
which is
a rational number.
is the
simplest form of the rationalizing factor of 
Solution 7
(i)
(ii)
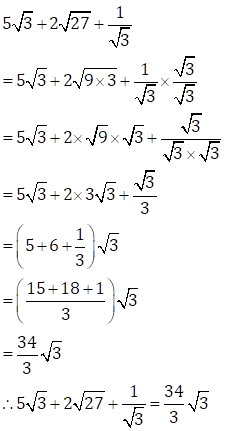
(iii)
(iv)
(v)
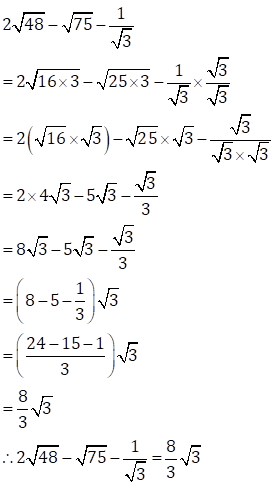
Solution 8
(i)
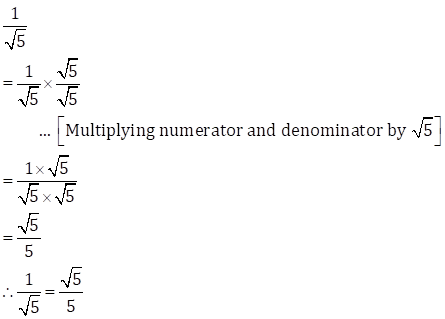
(ii)
(iii)
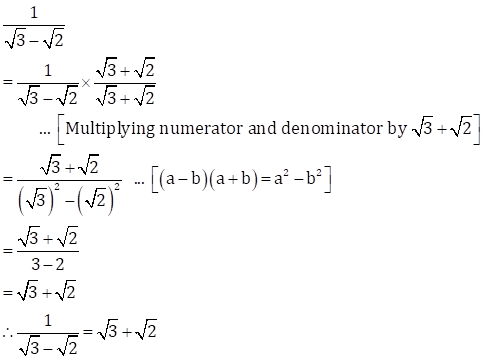
(iv)
(v)
