Class 9 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 3 - Polynomials

The power y in the second term is -1, which is a negative integer.

Thus, it is not a polynomial.

The power x in the second term 5√x is which is a decimal number.

Thus, it is not a polynomial.

For the expression x² + 7x + 9, the power of x in each term is a whole number and all the coefficients are real numbers.

Thus, it is a polynomial.

The power of m in the first term 2m^-2 is -2, which is a negative number.

Thus, it is not a polynomial.

10 is a constant number.

Thus, it is a polynomial.

Coefficient of m³ in the polynomial m³ is 1.

The coefficient of m³ in the polynomial is -√3.

The coefficient of m³ in the polynomial is

(i) Monomial with degree 7 is given by 5x⁷

(ii) Binomial with degree 35 is given by 2x + x³⁵

(iii) Trinomial with degree 8 is given by 2x² + 5x⁶ + 4x⁸

(i) √5 = √5x°

∴ Degree of the polynomial = 0

(ii) x^o

∴ Degree of the polynomial = 0

(iii) x²

∴ Degree of the polynomial = 2

(iv) √2m¹⁰ - 7

∴ Degree of the polynomial = 10

(v) 2p - √7

∴ Degree of the polynomial = 1

(vi) 7y - y³ + y⁵

The highest power of y is 5.

∴ Degree of the polynomial = 5

(vii) xyz + xy - z

Here, the sum of the powers of x, y and z in the term xyz is 1 + 1 + 1= 3.

And this is the highest sum of powers in the given polynomial.

∴ Degree of the polynomial = 3

(viii) m³n⁷ - 3m⁵n + mn

Here, the sum of the powers of m and n in the term m³n⁷ is 3 + 7 = 10.

And this is the highest sum of powers in the given polynomial.

∴ Degree of the polynomial = 10

In polynomial 2x² + 3x + 1, only one variable is involved and degree = 2

Thus, it is a quadratic polynomial.

In polynomial 5p, only one variable is involved and degree = 1

Thus, it is a linear polynomial.

In polynomial only one variable is involved and degree = 1

Thus, it is a linear polynomial.

In polynomial only one variable is involved and degree = 3

Thus, it is a cubic polynomial.

In polynomial a², only one variable is involved and degree = 2

Thus, it is a quadratic polynomial.

In polynomial 3r³, only one variable is involved and degree = 3

Thus, it is a cubic polynomial.

Given polynomial is m³ + 3 + 5m

It can be written in standard form as m³ + 5m + 3.

Given polynomial is

It can be written in standard form as .

Given polynomial is x³ - 2 = x³ + 0x² + 0x - 2

Its coefficient form is given by (1, 0, 0, -2).

Given polynomial is 5y = 5y + 0

Its coefficient form is given by (5, 0).

Given polynomial is 2m⁴ - 3m² + 7= 2m⁴ + 0m³ - 3m² + 0m + 7

Its coefficient form is given by (2, 0, -3, 0, 7).

Given polynomial is

Its coefficient form is given by

Number of coefficients = 3

∴ Degree of the polynomial = 3 - 1 = 2

Taking x as the variable, the standard form is x² + 2x + 3.

Number of coefficients = 5

∴ Degree of the polynomial = 5 - 1 = 4

Taking x as the variable, the standard form is 5x⁴ + 0x³ + 0x² + 0x - 1.

Number of coefficients = 4

∴ Degree of the polynomial = 4 - 1 = 3

Taking x as the variable, the standard form is -2x³ + 2x² - 2x + 2.

Number of trees in the village Lat = a

Number of trees increasing every year = b

∴ Number of trees after 'x' years = a + bx

∴ There will be (a + bx) trees in the village Lat after x years.

Total number of rows = x

Number of students in each row = y

∴ Total students = Total number of rows × Number of students in each row

= x × y

= xy

∴ There are in all 'xy' students for the parade.

Digit in tens place = m

Digit in units place = n

∴ The two digit number = (10 × digit in tens place) + digit in units place

= 10m + n

∴ The polynomial representing the two digit number is 10m + n.

(x³ - 2x² - 9) + (5x³ + 2x + 9)

= x³ - 2x² - 9 + 5x³ + 2x + 9

= (x³ + 5x³) - 2x² + 2x - 9 + 9

= 6x³ - 2x² + 2x

(-7m⁴ + 5m³ +√2) + (5m⁴ - 3m³ + 2m² + 3m - 6)

= -7m⁴ + 5m³ + √2 + 5m⁴ - 3m³ + 2m² + 3m - 6

= -7m⁴ + 5m⁴ + 5m³ - 3m³ + 2m² + 3m + √2 - 6

= -2m⁴ + 2m³ + 2m² + 3m + √2 - 6

(2y² + 7y + 5) + (3y + 9) + (3y² - 4y - 3)

= 2y² + 7y + 5 + 3y + 9 + 3y² - 4y - 3

= 2y² + 3y² + 7y + 3y - 4y + 5 + 9 - 3

= 5y² + 6y + 11

(x² - 9x + 3) - (-19x + √3 + 7x²)

= x² - 9x + √3 + 19x -√3- 7x²

= x² - 7x² - 9x + 19x + √3 -√3

= -6x² + 10x

(2ab² + 3a²b - 4ab) - (3ab - 8ab² + 2a²b)

= 2ab² + 3a²b - 4ab - 3ab + 8ab² - 2a²b

= 2ab² + 8ab² + 3a²b - 2a²b - 4ab - 3ab

= 10ab² + a²b - 7ab

(i)

(2x) × (x² - 2x - 1)

= 2x³ - 4x² - 2x

(ii)

(x⁵ - 1) × (x³ + 2x² + 2)

= x⁵(x³ + 2x² + 2) - 1(x³ + 2x² + 2)

= x⁸ + 2x⁷ + 2x⁵ - x³ - 2x² - 2

(iii)

(2y + 1) × (y² - 2y³ + 3y)

= 2y × (y² - 2y³ + 3y) + 1 × (y² - 2y³ + 3y)

= 2y³ - 4y⁴ + 6y² + y² - 2y³ + 3y

= -4y⁴ + 7y² + 3y

Here, x³ - 64 = x³ + 0x² + 0x - 64

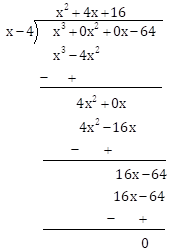
∴ Quotient = x² + 4x + 16 and Remainder = 0

Since, Dividend = Divisor × Quotient + Remainder

∴ x³ - 64 = (x - 4)(x² + 4x + 16) + 0

Here, 5x⁵ + 4x⁴ - 3x³ + 2x² + 2 = 5x⁵ + 4x⁴ - 3x³ + 2x² + 0x + 2

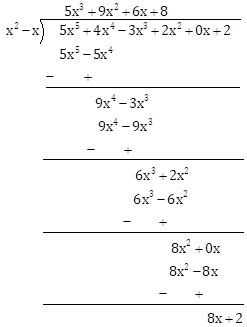
∴ Quotient = 5x³ + 9x² + 6x + 8 and Remainder = 8x + 2

Since, Dividend = Divisor × Quotient + Remainder

∴ 5x⁵ + 4x⁴ - 3x³ + 2x² + 2 = (x² - x)( 5x³ + 9x² + 6x + 8) + 8x + 2

Length of the rectangular farm = (2a² + 3b²) m

Breadth of the rectangular farm = (a² + b²) m

Area of the farm = length × breadth = (2a² + 3b²) × (a² + b²)

= 2a²(a² + b²) + 3b²(a² + b²)

= 2a⁴ + 2a²b² + 3a²b² + 3b⁴

= (2a⁴ + 5a²b² + 3b⁴) sq. m

∴ Area of the farm = (2a⁴ + 5a²b² + 3b⁴) sq. m … (i)

It is given that the farmer used a square shaped plot of the farm to build a house.

Side of the square shaped plot = (a² - b²) m

∴ Area of the plot = (side)²

= (a² - b²)²

= (a⁴ - 2a²b² + b⁴) sq. m

∴ Area of the plot = (a⁴ - 2a²b² + b⁴) sq. m … (ii)

∴ Area of the remaining farm = Area of the farm - Area of the plot

= (2a⁴ + 5a²b² + 3b⁴) - (a⁴ - 2a²b² + b⁴) … [From (i) and (ii)]

= 2a⁴ + 5a²b² + 3b⁴ - a⁴ + 2a²b² - b⁴

= 2a⁴ - a⁴ + 5a²b² + 2a²b² + 3b⁴ - b⁴

= a⁴ + 7a²b² + 2b⁴

∴ The area of the remaining farm is (a⁴ + 7a²b² + 2b⁴) sq. m.

Synthetic division:

Dividend = 2m² - 3m + 10

Coefficient form of dividend is (2, -3, 10)

Divisor = m - 5

Opposite of -5 is 5

Coefficient form of the quotient is (2, 7)

∴ Quotient = 2m + 7 and Remainder = 45

Linear method:

2m² - 3m + 10

To get 2m², multiply (m - 5) with 2m and add 10m

= 2m(m - 5) + 10m - 3m + 10

= 2m(m - 5) + 7m + 10

To get the term 7m, multiply (m - 5) by 7 and add 35

= 2m(m - 5) + 7(m - 5) + 35 + 10

= (m - 5)(2m + 7) + 45

∴ Quotient = 2m + 7 and Remainder = 45

Synthetic division:

Dividend = x⁴ + 2x³ + 3x² + 4x + 5

Coefficient form of dividend is (1, 2, 3, 4, 5)

Divisor = x + 2

Opposite of 2 is -2

Coefficient form of the quotient is (1, 0, 3, -2)

∴ Quotient = x³ + 3x - 2 and Remainder = 9

Linear method:

x⁴ + 2x³ + 3x² + 4x + 5

To get x⁴, multiply (x + 2) with x³ and subtract 2x³

= x³(x + 2) - 2x³+ 2x³ + 3x² + 4x + 5

= x³(x + 2) + 3x² + 4x + 5

To get the term 3x², multiply (x + 2) with 3x and subtract 6x

= x³(x + 2) + 3x(x + 2) - 6x + 4x + 5

= x³(x + 2) + 3x(x + 2) - 2x + 5

To get the term -2x, multiply (x + 2) with -2 and add 4

= x³(x + 2) + 3x(x + 2) - 2(x + 2) + 4 + 5

= x³(x + 2) + 3x(x + 2) - 2(x + 2) + 9

= (x + 2)(x³+ 3x - 2) + 9

∴ Quotient = x³ + 3x - 2 and Remainder = 9

Synthetic division:

Dividend = y³ - 216 = y³ + 0y² + 0y - 216

Coefficient form of dividend is (1, 0, 0, -216)

Divisor = y - 6

Opposite of -6 is 6

Coefficient form of the quotient is (1, 6, 36)

∴ Quotient = y³ + 6y + 36 and Remainder = 0

Linear method:

y³ - 216

To get y³, multiply (y - 6) with y² and add 6y²

= y²(y - 6) + 6y² - 216

To get the term 6y², multiply (y - 6) with 6y and add 36y

= y²(y - 6) + 6y(y - 6) + 36y - 216

To get the term 36y, multiply (y - 6) with 36 and 216

= y²(y - 6) + 6y(y - 6) + 36(y - 6) + 216 - 216

= y²(y - 6) + 6y(y - 6) + 36(y - 6)

= (y - 6)(y² + 6y + 36)

∴ Quotient = y² + 6y + 36 and Remainder = 0

Synthetic division:

Dividend = 2x⁴ + 3x³ + 4x - 2x² = 2x⁴ + 3x³ - 2x² + 4x + 0

Coefficient form of dividend is (2, 3, -2, 4, 0)

Divisor = x + 3

Opposite of 3 is -3

Coefficient form of the quotient is (2, -3, 7, -17))

∴ Quotient = 2x³ - 3x² + 7y - 17 and Remainder = 51

Linear method:

2x⁴ + 3x³ + 4x - 2x²

To get the term 2x⁴, multiply (x + 3) with 2x³ and subtract 6x³

= 2x³(x + 3) - 6x³ + 3x³ + 4x - 2x²

= 2x³(x + 3) - 3x³ + 4x - 2x²

To get the term -3x³, multiply (x + 3) with -3x² and add 9x²

= 2x³(x + 3) - 3x²(x + 3) + 9x² - 2x² + 4x

= 2x³(x + 3) - 3x²(x + 3) + 7x² + 4x

To get the term 7x², multiply (x + 3) with 7x and subtract 21x

= 2x³(x + 3) - 3x²(x + 3) + 7x(x + 3) - 21x + 4x

= 2x³(x + 3) - 3x²(x + 3) + 7x(x + 3) - 17x

To get the term -17x, multiply (x + 3) with -17 and add 51

= 2x³(x + 3) - 3x²(x + 3) + 7x(x + 3) - 17(x + 3) + 51

= (x + 3)(2x³ - 3x² + 7x - 17) + 51

∴ Quotient = 2x³ - 3x² + 7x - 17 and Remainder = 51

Synthetic division:

Dividend = x⁴ - 3x² - 8 = x⁴ + 0x³ - 3x² + 0x - 8

Coefficient form of dividend is (1, 0, -3, 0, -8)

Divisor = x + 4

Opposite of 4 is -4

Coefficient form of the quotient is (1, -4, 13, -52)

∴ Quotient = x³ - 4x² + 13x - 52 and Remainder = 200

Linear method:

x⁴ - 3x² - 8

To get the term x⁴, multiply (x + 4) with x³ and subtract 4x³

= x³(x + 4) - 4x³ - 3x² - 8

To get the term -4x³, multiply (x + 4) with -4x² and add 16x²

= x³(x + 4) - 4x²(x + 4) + 16x² - 3x² - 8

= x³(x + 4) - 4x²(x + 4) + 13x² - 8

To get the term 13x², multiply (x + 4) with 13x and subtract 52x

= x³(x + 4) - 4x²(x + 4) + 13x(x + 4) - 52x - 8

To get the term -52x, multiply (x + 4) with -52 and add 208

= x³(x + 4) - 4x²(x + 4) + 13x(x + 4) - 52(x + 4) + 208 - 8

= x³(x + 4) - 4x²(x + 4) + 13x(x + 4) - 52(x + 4) + 200

= (x + 4)(x³ - 4x² + 13x - 52) + 200

∴ Quotient = x³ - 4x² + 13x - 52 and Remainder = 200

Synthetic division:

Dividend = y³ - 3y² + 5y - 1

Coefficient form of dividend is (1, -3, 5, -1)

Divisor = y - 1

Opposite of -1 is 1

Coefficient form of the quotient is (1, -2, 3)

∴ Quotient = y² - 2y + 3 and Remainder = 2

Linear method:

y³ - 3y² + 5y - 1

To get the term y³, multiply (y - 1) with y² and add y²

= y²(y - 1) + y² - 3y² + 5y - 1

= y²(y - 1) - 2y² + 5y - 1

To get the term -2y², multiply (y - 1) with -2y and subtract 2y

= y²(y - 1) - 2y(y - 1)² - 2y + 5y - 1

= y²(y - 1) - 2y(y - 1)² + 3y - 1

To get the term 3y, multiply (y - 1) with 3 and add 3

= y²(y - 1) - 2y(y - 1)² + 3(y - 1) + 3 - 1

= y²(y - 1) - 2y(y - 1)² + 3(y - 1) + 2

= (y - 1)(y² - 2y + 3) + 2

∴ Quotient = y² - 2y + 3 and Remainder = 2

Let p(x) = x² - 5x + 5

Put x = 0 in the given polynomial

∴ p(0) = 0² - 5×0 + 5

= 0 - 0 + 5

= 5

∴ Value of the given polynomial at x = 0 is 5.

Given: p(y) = y² - 3√2y + 1

∴p(3√2) = (3√2y)² - (3√2y) × (3√2y) + 1

= (9 × 2) - (9 × 2) + 1

= 18 - 18 + 1

= 1

∴ p (3√2) = 1

Given: p(m) = m³ + 2m² - m + 10

∴ p(a) = a³ + 2(a)² - a + 10

= a³ + 2a² - a + 10

∴ p(a) = a³ + 2a² - a + 10 … (I)

Also, p(-a) = (-a)³ + 2(-a)² - (-a) + 10

= -a³ + 2a² + a + 10

∴ p(-a) = -a³ + 2a² + a + 10 … (II)

Adding (I) and (II)

∴ p(a) + p(-a) = a³ + 2a² - a + 10 + (-a³ + 2a² + a + 10)

= a³ - a³ + 2a² + 2a² - a + a + 10 + 10

= 4a² + 20

∴ p(a) + p(-a) = 4a² + 20

Given: p(y) = 2y³ - 6y² - 5y + 7

∴ p(2) = 2(2)³ - 6(2)² - 5(2) + 7

= 2×8 - 6×4 - 10 + 7

= 16 - 24 - 3

= -8 - 3

= -11

∴ p(2) = -11

Let p(x) = 2x - 2x³ + 7

At x = 3, the value of the polynomial is given by

p(3) = 2×3 - 2(3)³ + 7

= 2 × 3 - 2 × 27 + 7

= 6 - 54 + 7

= -48 + 7

= -41

∴ p(3) = -41

Let p(x) = 2x - 2x³ + 7

At x = -1, the value of the polynomial is given by

p(-1) = 2(-1) - 2(-1)³ + 7

= -2 × 1 - 2 × (-1) + 7

= -2 + 2 + 7

= 7

∴ p(-1) = 7

Let p(x) = 2x - 2x³ + 7

At x = 0, the value of the polynomial is given by

p(0) = 2(0) - 2(0)³ + 7

= 2 × 0 - 2 × 0 + 7

= 0 - 0 + 7

= 7

∴ p(0) = 7

Given: p(x) = x³

∴ p(1) = 1³ = 1

∴ p(1) = 1

p(0) = 0³ = 0

∴ p(0) = 0

p(-2) = (-2)³ = -8

∴ p(-2) = -8

Given: p(y) = y² - 2y + 5

∴ p(1) = 1² - 2(1) + 5

= 1 - 2 + 5

= 4

∴ p(1) = 4

p(0) = 0² - 2(0) + 5

= 0 - 0 + 5

= 5

∴ p(0) = 5

p(-2) = (-2)² - 2(-2) + 5

= 4 - (-4) + 5

= 4 + 4 + 5

= 13

∴ p(-2) = 13

Given: p(x) = x⁴ - 2x² - x

∴ p(1) = 1⁴ - 2(1)² - 1

= 1 - 2×1 - 1

= 1 - 2 - 1

= -2

∴ p(1) = -2

p(0) = 0⁴ - 2(0)² - 0

= 0 - 0 - 0

= 0

∴ p(0) = 0

p(-2) = (-2)⁴ - 2(-2)² - (-2)

= 16 - 2(4) + 2

= 16 - 8 + 2

= 10

∴ p(-2) = 10

Let p(m) = m³ + 2m + a

∴ p(2) = 2³ + 2(2) + a

= 8 + 4 + a

= 12 + a

∴ p(2) = 12 + a

Since, p(2) = 12

∴ 12 = 12 + a

∴ a = 12 - 12

∴ a = 0

Given: p(x) = mx² - 2x + 3

∴ p(-1) = m(-1)² - 2(-1) + 3

= m(1) + 2 + 3

= m + 5

∴ p(-1) = m + 5

Since, p(-1) = 7

∴ 7 = m + 5

∴ m = 7 - 5

∴ m = 2

Dividend = p(x) = x² - 7x + 9

Divisor = x + 1

∴ Take x = -1

∴ By Remainder theorem, we have

Remainder = p(-1)

Since, p(x) = x² - 7x + 9

∴ p(-1) = (-1)² - 7(-1) + 9

= 1 + 7 + 9

= 17

∴ Remainder = 17

Dividend = p(x) = 2x³ - 2x² + ax - a

Divisor = x - a

∴ Take x = a

∴ By Remainder theorem, we have

Remainder = p(a)

Since, p(x) = 2x³ - 2x² + ax - a

∴ p(a) = 2(a)³ - 2(a)² + a(a) - a

= 2a³ - 2a² + a² - a

= 2a³ - a² - a

∴ Remainder = 2a³ - a² - a

Dividend = p(x) = 54m³ + 18m² - 27m + 5

Divisor = m - 3

∴ Take m = 3

∴ By Remainder theorem, we have

Remainder = p(3)

Since, p(x) = 54m³ + 18m² - 27m + 5

∴ p(3) = 54(3)³ + 18(3)² - 27(3) + 5

= 54(27) + 18(9) - 27(3) + 5

= 1458 + 162 - 81 + 5

= 1544

∴ Remainder = 1544

Let p(y) = y³ - 5y² + 7y + m

Divisor = y + 2

∴ take y = -2

∴ By Remainder theorem, we have

Remainder = p(-2)

i.e. 50 = p(-2)

Since, p(y) = y³ - 5y² + 7y + m

∴ 50 = (-2)³ - 5(-2)² + 7(-2) + m

∴ 50 = -8 - 20 - 14 + m

∴ 50 = -42 + m

∴ m = 92

Dividend = p(x) = x² + 2x - 3

Divisor = x + 3

∴ take x = -3

∴ p(-3) = (-3)² + 2(-3) - 3

= 9 - 6 - 3

= 0

Since, p(-3) = 0

∴ By factor theorem, (x + 3) is a factor of the polynomial (x² + 2x - 3).

Let p(x) = x³ - mx² + 10x - 20

Since, (x - 2) is a factor of p(x)

∴ p(2) = 0

Now, p(2) = 2³ - m(2)² + 10(2) - 20

∴ 2³ - m(2)² + 10(2) - 20 = 0

∴ 8 - 4m + 20 - 20 = 0

∴ 8 - 4m = 0

∴ 4m = 8

∴ m = 2

Dividend = p(x) = x³ - x² - x - 1

Divisor = q(x) = x - 1

∴ take x = 1

∴ Remainder = p(1)

Since, p(x) = x³ - x² - x - 1

∴ p(1) = 1³ - 1² - 1 - 1

= 1 - 1 - 1 - 1

= -2

As p(1) ≠ 0

∴ By factor theorem, (x - 1) is not a factor of the polynomial x³ - x² - x - 1.

Dividend = p(x) = 2x³ - x² - 45

Divisor = q(x) = x - 3

∴ take x = 3

∴ Remainder = p(3)

Since, p(x) = 2x³ - x² - 45

∴ p(3) = 2(3)³ - 3² - 45

= 2×27 - 9 - 45

= 54 - 54

= 0

As p(3) = 0

∴ By factor theorem, (x - 3) is a factor of the polynomial 2x³ - x² - 45.

Dividend = p(x) = x³¹ + 31

Divisor = x + 1

∴ Take x = -1

∴ By Remainder theorem, we have

Remainder = p(-1)

Since, p(x) = x³¹ + 31

∴ p(-1) = (-1)³¹ + 31

= -1 + 31

= 30

∴ Remainder = 30

Let p(m) = m²¹ - 1 and q(m) = m²² - 1

(i)

Dividend = p(m) = m²¹ - 1

Divisor = m - 1

∴ take m = 1

∴ Remainder = p(1)

Since, p(m) = m²¹ - 1

∴ p(1) = (1)²¹ - 1

= 1 - 1

= 0

As p(1) = 0

∴ By factor theorem, (m - 1) is a factor of the polynomial m²¹ - 1.

(ii)

Dividend = q(m) = m²² - 1

Divisor = m - 1

∴ take m = 1

∴ Remainder = q(1)

Since, q(m) = m²² - 1

∴ q(1) = (1)²² - 1

= 1 - 1

= 0

As q(1) = 0

∴ By factor theorem, (m - 1) is a factor of the polynomial m²² - 1.

Let p(x) = nx² - 5x + m

Since, (x - 2) is a factor of p(x)

∴ p(2) = 0

Now, p(2) = n(2)² - 5(2) + m

∴ n(2)² - 5(2) + m = 0

∴ 4n - 10 + m = 0 … (I)

Since, x - is a factor of p(x)

Now,

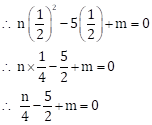
Multiplying both sides of the above equation by 4

∴ n - 10 + 4m = 0

∴ n = 10 - 4m … (II)

Substituting n = 10 - 4m in equation (I), we get

4(10 - 4m) - 10 + m = 0

∴ 40 - 16m - 10 + m = 0

∴ 30 - 15m = 0

∴ 15m = 30

∴ m = 2

Putting m = 2 in equation (II)

∴ n = 10 - 4(2)

∴ n = 10 - 8

∴ n = 2

Thus, m = n = 2

Given: p(x) = 2 + 5x

∴ p(2) = 2 + 5×2

= 2 + 10

= 12

∴ p(-2) = 2 + 5×(-2)

= 2 - 10

= -8

∴ p(1) = 2 + 5×1

= 2 + 5

= 7

∴ p(2) + p(-2) - p(1) = 12 - 8 - 7 = -3

Given: p(x) = 2x² - 5√3x + 5

∴ p(5√3) = 2(5√3)² - (5√3)(5√3) + 5

= 2(25 × 3) - (25 × 3) - (25 × 3) + 5

= 2 × 75 - 75 + 5

= 150 - 75 +5

= 80

∴ p(5√3) = 80

2x² + x - 1

= 2x² + 2x - x - 1

= 2x(x + 1) - (x + 1)

= (x + 1)(2x - 1)

So, (x + 1) and (2x - 1) are the factors of 2x² + x - 1.

2m² + 5m - 3

= 2m² + 6m - m - 3

= 2m(m + 3) - (m + 3)

= (m + 3)(2m - 1)

So, (m + 3) and (2m - 1) are the factors of 2m² + 5m - 3.

12x² + 61x + 77

= 12x² + 28x + 33x + 77

= 4x(3x + 7) + 11(3x + 7)

= (3x + 7)(4x + 11)

So, (3x + 7) and (4x + 11) are the factors of 12x² + 61x + 77.

3y² - 2y - 1

= 3y² - 3y + y - 1

= 3y(y - 1) + 1(y - 1)

= (y - 1)(3y + 1)

So, (y - 1) and (3y + 1) are the factors of 3y² - 2y - 1.

√3x² + 4x + √3

= √3x² + 3x + x + √3

= √3x(x + √3) + (x + √3)

= (x + √3)(√3x + 1)

So, (x +√3) and (√3x + 1) are the factors of √3x² + 4x + √3.

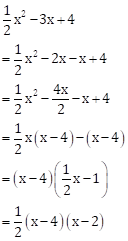
So, are the factors of

Let x² - 6x = m

∴ (x² - 6x)² - 8(x² - 6x + 8) - 64

= m² - 8(m + 8) - 64

= m² - 8m - 64 - 64

= m² - 8m - 128

= m² - 16m + 8m - 128

= m(m - 16) + 8(m - 16)

= (m - 16)(m + 8)

= (x² - 6x - 16)(x² - 6x + 8) … Replacing m with (x² - 6x)

= [x² - 8x + 2x - 16] [x² - 4x - 2x + 8]

= [x(x - 8) + 2(x - 8)] [x(x - 4) - 2(x - 4)]

= (x - 8) (x + 2) (x - 4) (x - 2)

∴ (x² - 6x)² - 8(x² - 6x + 8) - 64 = (x - 8) (x + 2) (x - 4) (x - 2)

Let x² - 2x = m

∴ (x² - 2x + 3) (x² - 2x + 5) - 35

= (m + 3) (m + 5) - 35

= m(m + 5) + 3(m + 5) - 35

= m² + 5m + 3m + 15 - 35

= m² + 8m - 20

= m² + 10m - 2m - 20

= m(m + 10) - 2(m + 10)

= (m + 10)(m - 2)

= (x² - 2x + 10) (x² - 2x - 2) … [Replacing m = x² - 2x]

∴ (x² - 2x + 3) (x² - 2x + 5) - 35 = (x² - 2x + 10) (x² - 2x - 2)

(y + 2) (y - 3) (y + 8) (y + 3) + 56

= (y + 2)(y + 3)(y - 3)(y + 8) + 56

= (y² + 3y + 2y + 6) (y² + 8y - 3y - 24) + 56

= (y² + 5y + 6) (y² + 5y - 24) + 56

= (m + 6) (m - 24) + 56 … [Putting y2 + 5y = m]

= m(m - 24) + 6(m - 24) + 56

= m² - 24m + 6m - 144 + 56

= m² - 18m - 88

= m² - 22m + 4m - 88

= m(m - 22) + 4(m - 22)

= (m - 22) (m + 4)

= (y² + 5y - 22)(y² + 5y + 4) … [Replacing m with y² + 5y]

= (y² + 5y - 22) (y² + 4y + y + 4)

= (y² + 5y - 22) [y(y + 4) + 1(y + 4)]

= (y² + 5y - 22) (y + 4) (y + 1)

∴ (y + 2) (y - 3) (y + 8) (y + 3) + 56 = (y² + 5y - 22) (y + 4) (y + 1)

Let y² + 5y = m

∴ (y² + 5y) (y² + 5y - 2) - 24

= m(m - 2) - 24

= m² - 2m - 24

= m² - 6m + 4m - 24

= m(m - 6) + 4(m - 6)

= (m - 6) (m + 4)

= (y² + 5y - 6) (y² + 5y + 4) … [Replacing m = y² + 5y]

= (y² + 6y - y - 6) (y² + 4y + y + 4)

= [y(y + 6) - 1(y + 6)] [y(y + 4) + 1(y + 4)]

= (y + 6) (y - 1) (y + 4) (y + 1)

∴ (y² + 5y) (y² + 5y - 2) - 24 = (y + 6) (y - 1) (y + 4) (y + 1)

(x - 3) (x - 4)² (x - 5) - 6

= (x - 3) (x - 5) (x - 4)² - 6

= (x² - 5x - 3x + 15) (x² - 8x + 16) - 6

= (x² - 8x + 15) (x² - 8x + 16) - 6

= (m + 15) (m + 16) - 6 … [Putting x² - 8x = m]

= m (m + 16) + 15 (m + 16) - 6

= m² + 16m + 15m + 240 - 6

= m² + 31m + 234

= m² + 18m + 13m + 234

= m(m + 18) + 13(m + 18)

= (m + 18) (m + 13)

= (x² - 8x + 18) (x² - 8x + 13) … [Replacing m = x² - 8x]

∴ (x - 3) (x - 4)² (x - 5) - 6 = (x² - 8x + 18) (x² - 8x + 13)

Let x² - x = m

∴ (x² - x)² - 8(x² - x) + 12 = m² - 8m + 12

= m² - 6m - 2m + 12

= m(m - 6) - 2(m - 6)

= (m - 6)(m - 2)

= (x² - x - 6)(x² - x - 2)

= [x² - 3x + 2x - 6][x² - 2x + x - 2]

= [x(x - 3) + 2(x - 3)] [x(x - 2) + (x - 2)]

= [(x - 3)(x + 2)] [(x - 2)(x + 1)]

= (x - 3)(x + 2)(x - 2)(x + 1)

∴ (x² - x)² - 8(x² - x) + 12 = (x - 3)(x + 2)(x - 2)(x + 1)

(x - 5)² - (5x - 25) - 24 = (x - 5)² - 5(x - 5) - 24

= m² - 5m - 24 …. (Putting x - 5 = m)

= m² - 8m + 3m - 24

= m(m - 8) + 3(m - 8)

= (m - 8)(m + 3)

= (x - 5 - 8)(x - 5 + 3) … (Replacing m with x - 5)

= (x - 13)(x - 2)

∴ (x - 5)² - (5x - 25) - 24 = (x - 13)(x - 2)

(D)

In the expression power of y is negative. So, it is not a polynomial.

In the expression x^√2 - 3x power of x in the first term is not a positive integer.

So, it is not a polynomial.

In the expression x^-2 + 7 power of y is negative. So, it is not a polynomial.

The expression is a polynomial as the power of x is a whole number.

(D)

Degree of the polynomial √7 is 0.

(C)

Degree of the 0 polynomial is undefined.

Highest power of the variable x is 3.

Therefore, degree of the 2x² + 5x³ + 7 is 3.

(C)

Here, x³ - 1 = x3 + 0x² + 0x - 1

∴ Its coefficient form is (1, 0, 0, -1).

(A)

Given: p(x) = x² - 7√7 x + 3

∴ p(7√7) = (7√7)² - 7√7(7√7) + 3

= (7√7)² - (7√7)² + 3

= 3

(D)

Let p(x) = 2x³ + 2x

At x = -1, we have

p(-1) = 2(-1)³ + 2(-1)

= 2(-1) - 2

= -2 - 2

= -4

∴ p(-1) = -4

(C)

Let p(x) = 3x² + mx

Since, x - 1 is a factor of the polynomial p(x)

∴ p(1) = 0

∴ 3(1)² + m × 1 = 0

∴ 3 × 1 + m = 0

∴ m = -3

(x² - 3) (2x - 7x³ + 4)

= x²(2x - 7x³ + 4) - 3(2x - 7x³ + 4)

= 2x³ - 7x⁵ + 4x² - 6x + 21x³ - 12

= -7x⁵ + 23x³ + 4x² - 6x - 12

Since the highest power of the variable x is 5.

∴ Degree of the polynomial = 5

In polynomial x + 5, degree = 1

∴ It is a linear polynomial.

(i) 5 + 3x⁴

Here, highest power of x is 4.

∴ Degree of the polynomial = 4

(ii) 7

The polynomial is a constant polynomial.

∴ Degree of the polynomial = 0

(iii) ax⁷ + bx⁹

Here, highest power of x is 9.

∴ Degree of the polynomial = 9

(i) 4x² + 7x⁴ - x³ - x + 9

Its standard form is 7x⁴ - x³ + 4x² - x + 9

(ii) p + 2p³ + 10p² + 5p⁴ - 8

Its standard form is 5p⁴ + 2p³ + 10p² + p - 8

(i) x⁴ + 16

Its index form is x⁴ + 0x³ + 0x² + 0x + 16

∴ Coefficient form of the polynomial is (1, 0, 0, 0, 16).

(ii) m⁵ + 2m² + 3m + 15

Its index form is m⁵ + 0m⁴ + 0m³ + 2m² + 3m + 15

∴ Coefficient form of the polynomial is (1, 0, 0, 2, 3, 15).

(i) (3, -2, 0, 7, 18)

Number of coefficients = 5

∴ Degree of the polynomial = 5 - 1 = 4

∴ The polynomial in index form = 3x⁴ - 2x³ + 0x² + 7x + 18

(ii) (6, 1, 0, 7)

Number of coefficients = 4

∴ Degree of the polynomial = 4 - 1 = 3

∴ The polynomial in index form = 6x³ + x² + 0x + 7

(iii) (4, 5, -3, 0)

Number of coefficients = 4

∴ Degree of the polynomial = 4 - 1 = 3

∴ The polynomial in index form = 4x³ + 5x² - 3x + 0

(7x⁴ - 2x³ + x + 10) + (3x⁴ + 15x³ + 9x² - 8x + 2)

= 7x⁴ - 2x³ + x + 10 + 3x⁴ + 15x³ + 9x² - 8x + 2

= 7x⁴ + 3x⁴ - 2x³ + 15x³ + 9x² + x - 8x + 10 + 2

= 10x⁴ + 13x³ + 9x² - 7x + 12

(3p³q + 2p²q + 7) + (2p²q + 4pq - 2p³q)

= 3p³q + 2p²q + 7 + 2p²q + 4pq - 2p³q

= 3p³q - 2p³q + 2p²q + 2p²q + 4pq + 7

= p³q + 4p²q + 4pq + 7

(5x² - 2y + 9) - (3x² + 5y - 7)

= 5x² - 2y + 9 - 3x² - 5y + 7

= 5x² - 3x² - 2y - 5y + 9 + 7

= 2x² - 7y + 16

(2x² + 3x + 5) - (x² - 2x + 3)

= 2x² + 3x + 5 - x² + 2x - 3

= 2x² - x² + 3x + 2x + 5 - 3

= x² + 5x + 2

(m³ - 2m + 3) × (m⁴ - 2m² + 3m + 2)

= m³(m⁴ - 2m² + 3m + 2) - 2m(m⁴ - 2m² + 3m + 2) + 3(m⁴ - 2m² + 3m + 2)

= m⁷ - 2m⁵ + 3m⁴ + 2m³ - 2m⁵ + 4m³ - 6m² - 4m + 3m⁴ - 6m² + 9m + 6

= m⁷ - 2m⁵ - 2m⁵ + 3m⁴ + 3m⁴ + 2m³ + 4m³ - 6m² - 6m² + 9m - 4m + 6

= m⁷ - 4m⁵ + 6m⁴ + 6m³ - 12m² + 5m + 6

(5m³ - 2) × (m² - m + 3)

= 5m³(m² - m + 3) - 2(m² - m + 3)

= 5m⁵ - 5m⁴ + 15m³ - 2m² + 2m - 6

Dividend = 3x³ - 8x² + x + 7

Coefficient form of dividend is (3, -8, 1, 7)

Divisor = x - 3

Opposite of -3 is 3

Coefficient form of the quotient is (3, 1, 4)

∴ Quotient = 3x² + x + 4 and Remainder = 19

Let p(x) = x³ - 2mx + 21

Since, (x + 3) is the factor of p(x).

∴ p(-3) = 0

As p(x) = x³ - 2mx + 21

∴ p(-3) = (-3)³ - 2m(-3) + 21

∴ 0 = -27 + 6m + 21

∴ 6m - 6 = 0

∴ 6m = 6

∴ m = 1

∴ x + 3 is the factor of the polynomial x³ - 2mx + 21 for m = 1.

Total population of villages at the end of 2016

= (5x² - 3y²) + (7y² + 2xy) + (9x² + 4xy)

= 5x² + 9x² - 3y² + 7y² + 2xy + 4xy

= 14x² + 4y² + 6xy … (i)

Total number of persons who went to other village at the beginning of 2017

= (x² + xy - y²) + (5xy) + (3x² + xy)

= x² + 3x² - y² + xy + 5xy + xy

= 4x² - y² + 7xy … (ii)

Remaining total population of villages = Total population at the end of 2016 - total number of persons who went to other village at the beginning of 2017

= 14x² + 4y² + 6xy - (4x² - y² + 7xy) … [From (i) and (ii)]

= 14x² + 4y² + 6xy - 4x² + y² - 7xy

= 14x² - 4x² + 4y² + y² + 6xy - 7xy

= 10x² + 5y² - xy

∴ The remaining total population of the three villages is 10x² + 5y²- xy.

Let p(x) = bx² + x + 5 and q(x) = bx³ - 2x + 5

When polynomial bx² + x + 5 is divided by x - 3, the remainder is m

By remainder theorem, we have

Remainder = p(3) = m

Since, p(x) = bx² + x + 5

∴ p(3) = b(3)² + 3 + 5

∴ m = 9b + 8

∴ m = 9b + 8 … (I)

When polynomial bx³ - 2x + 5 is divided by x - 3, the remainder is n

By remainder theorem, we have

Remainder = q(3) = n

Since, q(x) = bx³ - 2x + 5

∴ q(3) = b(3)³ - 2(3) + 5

∴ n = 27b - 6 + 5

∴ n = 27b - 1 … (II)

Since, m - n = 0

From (I) and (II), we get

9b + 8 - (27b - 1) = 0

∴ 8 + 1 - 27b + 9b = 0

∴ 9 - 18b = 0

∴ 18b = 9

(8m² + 3m - 6) - (9m - 7) + (3m² - 2m + 4)

= 8m² + 3m - 6 - 9m + 7 + 3m² - 2m + 4

= 8m² + 3m² + 3m - 9m - 2m - 6 + 7 + 4

= 11m² - 8m + 5

Let the required polynomial be p(x).

∴ (x² + 13x + 7) - p(x) = 3x² + 5x - 4

∴ p(x) = (x² + 13x + 7) - (3x² + 5x - 4)

= x² + 13x + 7 - 3x² - 5x + 4

= x² - 3x² + 13x - 5x + 7+ 4

= -2x² + 8x + 11

∴ -2x² + 8x + 11 must be subtracted from x² + 13x + 7 to get 3x² + 5x - 4.

Let the required polynomial be P.

∴ (4m + 2n + 3) + P = 6m + 3n + 10

∴ P = 6m + 3n + 10 - (4m + 2n + 3)

= 6m + 3n + 10 - 4m - 2n - 3

= 6m - 4m + 3n - 2n + 10 - 3

= 2m + n + 7

∴ 2m + n + 7 must be added to 4m + 2n + 3 to get 6m + 3n + 10.