Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 2: Parallel lines and transversals
Parallel lines and transversals Exercise Ex. 2.1
Solution 1
By the definition of corresponding angles, a pair of angles is in the same direction and the other arms are on the same side of the transversal.
Hence, from the diagram,
(1) ∠ p and ∠ w
(2) ∠ q and ∠ x
(3) ∠ r and ∠ y
(4) ∠ s and ∠ z
By definition of alternate interior angles, a pair of angles which are at the inner side of given lines and on the opposite side of the transversal
Hence, from the diagram,
(5) ∠ s and ∠ x
(6) ∠ w and ∠ r
Solution 2(1)
By definition of interior alternate angles, a pair of angles which are at the inner side of lines and on the opposite side of transversal.
Hence, from the diagram,
∠ c and ∠ e
∠ b and ∠ h
Solution 2(2)
By the definition of corresponding angles, a pair of angles which are in the same direction and the other arms are on the same side of the transversal.
Hence, from the diagram,
∠ a and ∠ e
∠ c and ∠ g
∠ b and ∠ f
∠ d and ∠ h
Solution 2(3)
By the definition of interior angles, a pair of angles on the same side of the transversal and inside the given lines is called a pair of interior angles.
Hence, from the diagram,
∠ c and ∠ h
∠ b and ∠ e
Parallel lines and transversals Exercise Ex. 2.2
Solution 1(1)
From the diagram,
Line m || line n and p is a transversal where 3x and x are interior angles and sum of interior angles is 180˚.
∴ 3x + x = 180˚
∴ 4x = 180˚
∴ x = 45˚
Solution 1(2)
Name the remaining angles and points as below in the diagram.
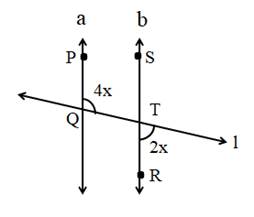
From the diagram,
Line a || line b and line l is a transversal.
∠ PQT = ∠ QTR = 4x (Alternate angles)
∠ QTR + 2x = 180˚ (Linear pair of angles)
∴ 4x + 2x = 180˚
∴ 6x = 180˚
∴ x = 30˚
Solution 2
Name the remaining angles and points as below in the diagram.
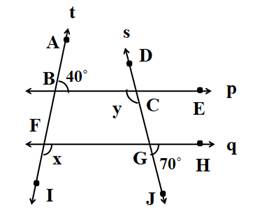
From the diagram,
Line p || line q, line t and s are transversals.
∠ ABC = 40˚
∠ ABC + ∠ CBF = 180˚……(Linear pair of angles)
∴ 40˚ + ∠ CBF = 180˚
∴ ∠ CBF = 180˚ ‒ 40˚
∴ ∠ CBF = 140˚
∴ ∠ CBF = ∠ x = 140˚…….(Corresponding angles)
∠ HGJ = 70˚
∠ HGJ + ∠ JGF = 180˚……..(Linear pair of angles)
∴ 70˚ + ∠ JGF = 180˚
∴ ∠ JGF = 180˚ ‒ 70˚
∴ ∠ JGF = 110˚
∴ ∠ JGF = ∠ y = 110˚……(Corresponding angles)
∠ x = 140˚, ∠ y = 110˚
Solution 3
Name the remaining angles and points as below in the diagram.
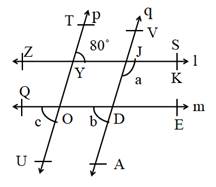
∠ TYJ + ∠ VJY = 180˚………….(Interior angles)
∴ 80˚ + ∠ VJY = 180˚
∴ ∠ VJY = 180˚ ‒ 80˚
∴ ∠ VJY = 100˚
∴ ∠ VJY = ∠ DJK = ∠ a = 100˚…..(Vertically opposite angles)
a + ∠ JDE = 180˚………….(Interior angles)
∴ 100˚ + ∠ JDE = 180˚
∴ ∠ JDE = 180˚ ‒ 100˚
∴ ∠ JDE = 80˚
∠ JDE = ∠ b = 80˚………(Vertically opposite angles)
∠ b = ∠ c = 80˚………….(Corresponding angles)
∠ a = 100˚, ∠ b = ∠ c = 80˚
Solution 4
From the diagram,
Line a and line b are parallel.
Line l is a transversal.
∠ x = 105˚……………..(Corresponding angles)
∠ x = ∠ y = 105˚……….(Vertically opposite angles)
105˚ +∠ z = 180˚………(Linear pair of angles)
∴ ∠ z = 180˚ ‒ 105˚
∴ ∠ z = 75˚
Solution 5
Name the remaining angles and points as below in the diagram.
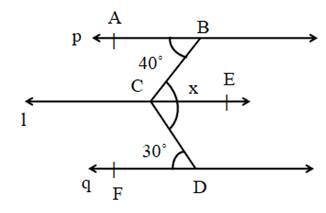
Line p || line l || line q where BC is transversal
Consider, line p || line l
∠ ABC = 40˚
∠ ABC = ∠ BCE = 40˚…..…(i) (alternate angles)
Consider, line l || line q where CD is transversal
∠ CDF = ∠ DCE = 30˚….…(ii) (Alternate angles)
∠ x = ∠ BCE + ∠ DCE = 40˚ + 30˚ = 70˚
Parallel lines and transversals Exercise Ex. 2.3
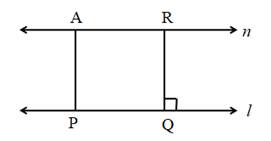
Solution 1
Steps of Construction:
1. Draw line l.
2. Take a point A outside the line l.
3. Draw a seg AP ⊥ line l.
4. Take another point Q on the line l.
5. Draw seg QR ⊥ line l where l(AP) = l(RQ)
6. The line n passing through the point A and R is parallel to the line l.
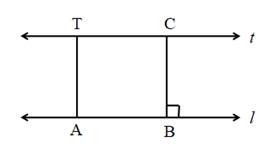
Solution 2
Steps of construction:
1. Draw line l.
2. Take a point T outside the line l.
3. Draw a seg TA ⊥ line l.
4. Take the point B, draw seg BC ⊥ line l such that l(TA) = l(CB)
5. The line t passing through the point T and C is parallel to the line l.
Solution 3
Steps of construction:
1. Draw line m.
2. Take two points X and Y on the line m.
3. Draw perpendicular to the line m from points X and Y.
4. On the perpendicular lines take point A and B at a distance of 4 cm from X and Y respectively.
5. Draw line n.
6. Line n
7. Line n is a line parallel to the line l at a distance 4 cm

