Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 18: Miscellaneous Excercise 1
Miscellaneous Excercise 1 Exercise Misc. Ex. 1
Solution 1(1)
(B)
From the diagram, we can observe that side PQ || side SR.
Solution 1(2)
(B)
Diagonals of a rhombus are perpendicular bisectors of each other.
Solution 1(3)
(D)
= 
Solution 2
(1)
5832 = 3 × 1944
= 3 × 3 × 648
= 3 × 3 × 3 × 216
= 3 × 3 × 3 × 3 × 72
= 3 × 3 × 3 × 3 × 2 × 36
= 3 × 3 × 3 × 3 × 2 × 2 × 18
= 3 × 3 × 3 × 3 × 2 × 2 × 2 × 9
= 3 × 3 × 3 × 3 × 2 × 2 × 2 × 3 × 3
= 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2 × 2
= 33 × 33 × 23
= (3 × 3 × 2)3
= 183
(2)
4096 = 2 × 2048
= 2 × 2 × 1024
= 2 × 2 × 2 × 512
= 2 × 2 × 2 × 2 × 256
= 2 × 2 × 2 × 2 × 2 × 128
= 2 × 2 × 2 × 2 × 2 × 2 × 64
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 32
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 16
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= (2 × 2 × 2 × 2)3
= 163
Solution 3
Given: m 
n
∴ m = kn, where k is a constant of variation
Also, n = 15 then m = 25
Hence, 25 = 15k
∴ k = 
= 
∴ Equation of variation is m = n
(1)
When n = 87
∴ m = × 87 = 5 ×
29 = 145
When n = 87 then m = 145
(2)
When m = 155 then n = ?
∴ 155 = n
∴ n = 155 × 
= 31 × 3 = 93
When m = 155 then m = 93
Solution 4
Since, y varies inversely with x
∴ y α 
∴ y = 
∴ k = xy
If y = 30 then x = 12
∴ k = 30 × 12 = 360
∴ Equation of variation is xy = 360
(1)
When x = 15, y = ?
15y = 360
∴ y = 24
When x = 15 then y = 24
(2)
When y = 18, x = ?
18x = 360
∴ x = 20
When y = 18 then x = 20
Solution 5
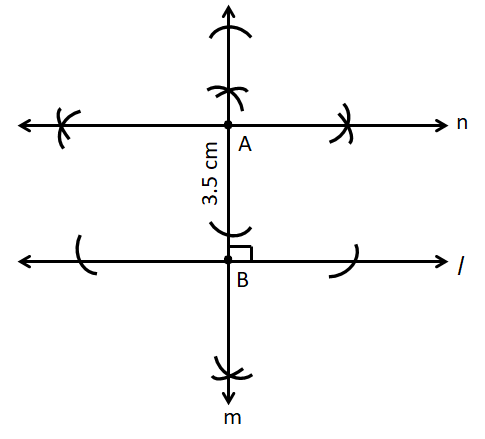
Solution 6
The number 
is 7th root of 5th
power of 256.
Solution 7
(1)
Using formula,
(x + a)(x + b) = x2 + (a + b)x + ab
(5x - 7)(5x - 9)
= (5x)2 + (-7 - 9)5x + (-7)×(-9)
= 25x2 - 80x + 63
(2)
Using formula,
(a - b)3 = a3 - 3a2b+ 3ab2 - b3
Where a = 2x, b = 3y
(2x - 3y)3 = (2x)3 - 3 × (2x)2 × 3y + 3 × 2x × (3y)2 - (3y)3
= 8x3 - 3 × 4x2 × 3y + 6x × 9y2 - 27y3
= 8x3 - 36x2y + 54xy2 - 27y3
(3)
Using formula,
(a + b)3 = a3 + 3a2b+ 3ab2 + b3
Solution 8
Steps of construction:
1. Draw ∆STV, TV = 5 cm, ST = 4 cm, ∠STV = 120˚
2. Draw perpendicular bisectors of seg ST, seg TV and Seg SV and name their midpoints such as X, Y, Z respectively.
3. Join SY, TZ, VX.
4. Name the intersection of these perpendiculars as G.
Solution 9
Orthocentre is the point of concurrency of the altitudes of a triangle.
Solution 10
We know that speed and distance are in inverse proportion.
∴ y α
∴ y =
∴ k = xy
If x = 48 then y = 5
∴ k = 48 × 5 = 240
∴ Equation of variation is xy = 240
Now, speed is reduced by 8 km/hr i.e. speed = 48 - 8 = 40 km/hr
If x = 40 then y = ?
Since, xy = 240
∴ 40y = 240
∴ y = 6
∴ The bus will take 6 hours to travel.
Solution 11
Given that ∆ABC, seg AD and seg BE are medians and G is the centroid.
We know that centroid divides median in the ratio 2:1.
∴ AG = 
AD
∴ 5 = AD
∴ AD = 5 × 
= 7.5 cm
Also, GD = 
AD = × 7.5 = 2.5 cm
Now, GE = BE
∴ 2 = BE
∴ BE = 2 × 3 = 6 cm
Solution 12
(1)
(2)
(3)
(4)
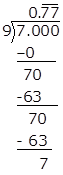
Solution 13
(1)
2y2 - 11y + 5
= 2y2 - 10y - y + 5
= 2y(y - 5) - (y - 5)
= (y - 5)(2y - 1)
(2)
x2 - 2x - 80
= x2 - 10x + 8x - 80
= x(x - 10) + 8(x - 10)
= (x - 10)(x + 8)
(3)
3x2 - 4x + 1
= 3x2 - 3x - x + 1
= 3x(x - 1) - (x - 1)
= (x - 1)(3x - 1)
Solution 14
The discount on marked price is 15%.
It means if the marked price is Rs. 100 then its selling price is
100 - 15 = Rs. 85
When marked price is Rs. 50,000 then selling price be Rs. x.
∴ 
∴ x = 
× 50000 =
42500
∴ Price of the TV set for the customer is Rs. 42,500.
Solution 15
Price of flat is Rs. 88,00,000.
Commission on flat is 2%.
Commission = 
× 88,00,000 =
1,76,000
Commission received from both buyer and seller
= 1,76,000 + 1,76,000
= Rs. 3,52,000
Solution 16
Steps of construction:
1. Draw seg DC = 5.5 cm
2. Draw ray DA and CB at angles 45˚ and 135˚ respectively.
3. Taking centres C and D and radius 4 cm, draw two arcs, one with D and other wth C respectively.
4. Name the points of intersection of the arcs with the rays as A and B.
5. Join A and B.
6. ABCD is the required parallelogram.
Solution 17
Line l || line m and line p is the transversal
∴ a = 78˚ … Corresponding angles
Also, line p || line q and line m is the transversal
∴ ∠a = ∠d = 78˚ … Corresponding angles
We know that sum of interior angles is 180˚
∴ ∠c + ∠d = 180˚
∴ ∠c + 78˚ = 180˚
∴ ∠c = 180˚ - 78˚ = 102˚
Now, ∠b and ∠d are vertically opposite angles
Thus, ∠b = ∠d = 78˚