Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 17: Circle : Chord and Arc
Circle : Chord and Arc Exercise Ex. 17.1
Solution 1
We know that perpendicular drawn from the centre of a circle to the chord, bisects the chord.
Seg PQ ⟂ chord AB.
Hence, AQ = BQ
Given that AB = 13 cm
![]()
![]() .5
cm
.5
cm
Solution 2
We know that perpendicular drawn from the centre of a circle to the chord, bisects the chord.
Seg OP ⟂ chord CD
Hence, CP = DP = ![]()
CP = DP = ![]()
In right angled ∆ OPD,
OP2 + PD2 = OD2
∴ OP2 = OD2 - PD2
= 252 - 242
= 625 - 576
= 49
OP2 = 49
∴OP = 7 cm
Hence, the distance of a chord from the centre is 7 cm.
Solution 3
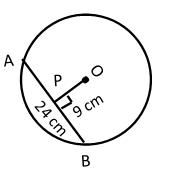
We know that perpendicular drawn from the centre of a circle to the chord, bisects the chord.
Seg OP ⟂ chord AB
Hence, PA = PB = ![]()
PA = PB = ![]()
OB = OA = 9 cm = radius
In right angled ∆ OPB,
OB2 = OP2 + PB2
= 122 + 92
= 144 + 81
= 225
OB2 = 225
∴OB = 15 cm
Radius of the circle is 15 cm.
Solution 4

In the given circle XY is a chord and CA ⟂ chord XY.
We know that perpendicular drawn from the centre of a circle to the chord, bisects the chord.
Seg CA ⟂ chord XY
Hence, XA = YA = ![]()
XA = YB = ![]()
CX = CY = 10 cm = radius
In right angled ∆ CAX,
CX2 = CA2 + AX2
CA2 = CX2 - AX2
= 102 - 62
= 100 - 36
= 64
CA2 = 64
∴ CA = 8 cm
The distance of the chord from the centre is 8 cm.
Circle : Chord and Arc Exercise Ex. 17.2
Solution 1
Given that chord PQ ⟂ chord RS
∠ PCS = ∠ SCQ = ∠ RCQ = ∠ PCR = 90"
m(arc PS) = ∠ PCS = 90" …(i)
m(arc SQ) = ∠ SCQ = 90" ….(ii)
m(arc SQ) = m(arc PS)
∴ arc SQ = arc PS
Similarly,
Arc PS ≅ arc PR ≅ arc RQ
Solution 2
We know that measure of central angle is equal to measure of corresponding arc.
m(arc AB) = ∠AOB …(i)
m(arc CD) = ∠ COD …(ii)
m(arc AM) = ∠ MOA = 100˚
m(arc NB) = ∠ BON = 35˚
m(arc MD) = ∠ MOD = 100˚
m(arc NC) = ∠ NOC = 35˚
seg MN is diameter of a circle.
∴ m(arc MA) + m(arc AB) + m(arc BN) = 180"
∴ 100˚ + m(arc AB) + 35˚ = 180"
∴ m(arc AB) = 180˚ - 100˚ - 35˚ = 45˚ …(iii)
Similarly, arc MDN is semicircular arc.
m(arc AM) + m(arc DC) + m(arc NC) = 180˚
∴ 100˚ + m(arc DC) + 35˚ = 180˚
∴ m(arc DC) = 180˚ - 100˚ - 35˚ = 45˚ …(iv)
From (iii) and (iv)
m(arc AB) = m(arc DC)
arc AB ≅ arc DC
From (i) and (ii)
m(arc AB) = ∠ AOB = 45˚
m(arc CD) = ∠ COD = 45˚
∴ ∠ AOB = ∠ COD = 45˚
m(arc AB) = m(arc CD)
Chord AB = chord CD
Corresponding chords of congruent arc are congruent.
∴ Chord AB ≅ chord CD
