Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 15: Area
Area Exercise Ex. 15.1
Solution 1
Given that base of parallelogram is 18 cm and height is 11 cm.
Area of parallelogram = base of parallelogram × height of parallelogram
= 18 × 11
= 198 cm2
∴ The area of a parallelogram is 198 cm2.
Solution 2
Given that area of parallelogram is 29.6 sq cm and base of parallelogram is 8 cm.
Area of parallelogram = 29.6
∴ Base × height = 29.6
∴ 8 × height = 29.6
∴ Height = ![]()
∴ The height of a parallelogram is 3.7 cm.
Solution 3
Given that area of parallelogram is 83.2 sq cm and height of parallelogram is 6.4 cm.
Since, Area of parallelogram = 83.2
∴ Base × height = 83.2
∴ Base × 6.4 = 83.2
∴ Base = ![]()
∴ The base of a parallelogram is 13 cm.
Area Exercise Ex. 15.2
Solution 1
The lengths of diagonals of a rhombus are 15 cm and 24 cm.
Area of a rhombus
= ![]()
= ![]()
= 15 ![]() 12
12
= 180 cm2
∴ Area of rhombus is 180 cm2.
Solution 2
The lengths of diagonals of a rhombus are 16.5 cm and 14.2 cm.
Area of rhombus =
![]()
= ![]()
= 7.1 ![]() 16.5
16.5
= 117.15 cm2
∴ Area of rhombus is 117.15 cm2.
Solution 3
Here, perimeter of a rhombus = 100 cm and length of one diagonal = 48 cm.
Since, the four sides of a rhombus are equal.
∴ The length of a
rhombus is ![]() .
.
Consider, a rhombus PQRS where diagonals interest at O.

Here, point O bisects both the diagonals PR and QS at right angles.
i.e. OS = OQ and OP = OR
∴ PO = ![]() =
= ![]()
Now, in right angled ∆POQ,
(PO)2 + (OQ)2 = (PQ)2 … Pythagoras theorem
∴ (24)2 + (OQ)2 = (25)2
∴ OQ2 = (25)2 - (24)2
∴ OQ2 = 625 - 576
∴ OQ2 = 49 cm2
∴ OQ = 7 cm
∴ QS = 2 × OQ = 2 × 7 = 14 cm
∴ The lengths of diagonals of a rhombus are 48 cm and 14 cm.
Area of rhombus =
![]()
= ![]()
= ![]()
= 336 cm2
∴ Area of rhombus is 336 cm2.
Solution 4
Given: Length of a diagonal = 30 cm and area of a rhombus = 240 sq. cm
Let the length of the other diagonal of a rhombus be x cm.
Area of a rhombus = ![]()
∴ 240 = 15x
∴ 15x = 240
∴ x = 16 cm
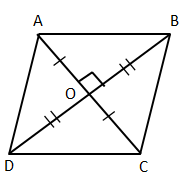
Consider, a rhombus ABCD where diagonals interest at O.
The diagonals of a rhombus intersect at O where point O bisects both the diagonals at right angles.
i.e. OD = OB and OA = OC
Now, AC = 30 cm and BD = 16 cm
OA = ![]()
∴ OA = ![]()
Similarly, OB = ![]()
∴ OB = ![]()
In right angled ∆AOB,
AB2 = AO2 + OB2
∴ AB2 = 152 + 82
∴ AB2 = 225 + 64
∴ AB2 = 289
∴ AB = 17 cm
The length of the side of a rhombus is 17 cm.
∴ Perimeter of a rhombus is 4 × side = 4 × 17 = 68 cm
Area Exercise Ex. 15.3
Solution 1
In □ABCD, l (AB) = 13 cm, l (DC) = 9 cm, l (AD) = 8 cm
Here, AB and DC are parallel sides and height = AD = 8 cm
Area of trapezium = ![]()
= ![]()
= ![]()
= 11 ![]()
= 88 cm2
∴ Area of trapezium is 88 cm2.
Solution 2
Lengths of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of trapezium
= ![]()
= ![]()
= ![]()
= 10 ![]()
= 42 cm2
∴ Area of trapezium is 42 cm2.
Solution 3

Let QN ⟂ NR.
From the given figure, seg PM ⟂ seg SR and seg QN ⟂ seg SR
Thus, side PQ || side MN
∴ □PQNM is a rectangle.
PQ = MN = 7 cm, PM = QN = 4 cm … (Opposite sides of a rectangle)
In right angled triangle ∆SMP and ∆RNQ,
PS = QR … (Opposite sides of an isosceles trapezium)
PM = QN = 4 cm and SM = NR = 3 cm
SR = SM + MN + NR (S - M - N - R)
= 3 + 7 + 3 = 13 cm
Area of trapezium = ![]()
= ![]()
= ![]()
= ![]()
= 10 ![]()
= 40 cm2
∴ Area of trapezium is 40 cm2.
Area Exercise Ex. 15.4
Solution 1
Let sides of a triangle be a = 45 cm, b = 39 cm, c = 42 cm.
Semi-perimeter (s)
= ![]()
Area of triangle
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= 9 × 3 × 7 × 4
= 27 × 28
= 756 cm2
∴ Area of triangle is 756 cm2.
Solution 2
In ∆PSR, PS ⟂ SR, using Pythagoras theorem,
PR2 = PS2 + SR2
= 362 + 152
= 1296 + 225
= 1521
∴ PR2 = 1521 cm2
∴ PR = 39 m … (i)
In ∆PSR,
Area of ∆PSR = ![]()
![]()
= ![]()
= 270 m2
In ∆PQR,
PQ = a = 56 m, QR = b = 25 m, PR = c = 39 m
∴ Semi-perimeter
(s) = ![]()
Area of triangle
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= 5 × 4 × 7 × 3
= 20 × 21
= 420 cm2
∴ Area of □ ABCD = area of ∆PSR + area of ∆PQR
= 270 + 420
= 690 cm2
Solution 3
In right angled triangle ∆BAD,
Base = AD = 9 m, height = AB = 40 m
∴ Area of ∆BAD = ![]()
= 9 × 20
= 180 m2
In ∆BDC,
Base = DC = 60 m, height = BT = 13 m
∴ Area of ∆BDC = ![]()
= 30 × 13
= 390 m2
Area of □ABCD = Area of ∆BAD + Area of ∆BDC
= 180 + 390
= 570 m2
Area Exercise Ex. 15.5
Solution 1(1)
In ∆ PAQ,
Base = PA = 30 m, height = QA = 50
Area of ∆ PAQ =
= 15 × 50
= 750 sq. m
In trapezium QACR, AQ and CR are parallel sides where AQ = 50 m, CR = 25 m and height = h = AC = AB + BC = 30 + 30 = 60 m
Area of trapezium QACR =
=
= 75 = = = 24
= 216 sq. m
In ∆ DEC,
Area of ∆ DEC =
= 14 = = = = 2 4 2
= 336 sq. m
Area of plots
= A(∆ ABE) + A(∆ BCE) + A(∆ EDC)
= 216 + 336 + 224
= 776 sq. m
Area Exercise Ex. 15.6
Solution 1(1)
Given that radius of a circle = r = 28 cm
Area of circle ![]()
=
![]()
= 22 × 4 × 28
= 2464 cm2
Solution 1(2)
Given that radius of a circle = r = 10.5 cm
Area of circle ![]()
= ![]()
= 22 × 1.5 × 28
= 346.5 cm2
Solution 1(3)
Given that radius of a circle = r = 17.5 cm
Area of circle ![]()
= ![]()
= 22 × 2.5 × 17.5
= 962.5 cm2
Solution 2(1)
Given that area of a circle = 176 sq cm
Since, Area of
circle ![]()
![]()
![]()
∴ r2 =
176 × ![]()
∴ r2 = 56
∴ r = ![]()
∴ Diameter = 2r =
2![]() cm
cm
Solution 2(2)
Given that area of a circle = 394.24 sq. cm
Since, Area of
circle ![]()
![]()
![]()
∴ r2 =
394.24 × ![]()
∴ r2 = 125.44
∴ r = ![]() = 11.2
= 11.2
∴ Diameter = 2r =
2 ![]() = 22.4 cm
= 22.4 cm
Solution 2(3)
Given that area of a circle = 12474 sq. cm
Since, Area of
circle ![]()
![]()
![]()
∴ r2 =
12474 × ![]()
∴ r2 = 3969
∴ r = ![]() = 63
= 63
∴ Diameter = 2r =
2 ![]() = 126 cm
= 126 cm
Solution 3
Diameter of a garden = d = 42 m
∴ Radius of inner
circle (r) = ![]()
Radius of outer circle (R) = 21 + width of a road
= 21 + 3.5
= 24.5 m
Area of a road = area of outer circle - area of inner circle
= ![]() -
- ![]()
= ![]() -
-![]()
= ![]()
= ![]()
= ![]()
= 500.50 sq. m
Solution 4
Circumference of a circle = 88 cm … (Given)
∴ 2![]() = 88
= 88
∴ ![]() = 88
= 88
∴ r = ![]() = 14
= 14
∴ r = 14 cm
∴ Area of a
circle = ![]() =
= ![]() = 616 sq. cm
= 616 sq. cm
