Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 4: Altitudes and Medians of a triangle
Altitudes and Medians of a triangle Exercise Ex. 4.1
Solution 1
In Δ LMN, segment LX is an altitude and segment LY is a median.
Solution 2
Steps of Construction:
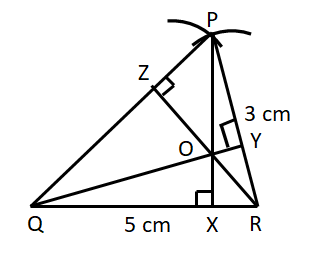
1. Draw any acute angled ∆ PQR
2. Draw perpendicular to PQ from the vertex R using a set square and it meets side PQ as Z. Seg RZ is altitude on side PQ.
3. Similarly draw an altitudes QY and PX on side PR and QR respectively.
4. Seg PX, seg QY and seg RZ are altitudes of a triangle PQR and the point of concurrence is 'O'.
Solution 3
Steps of construction:
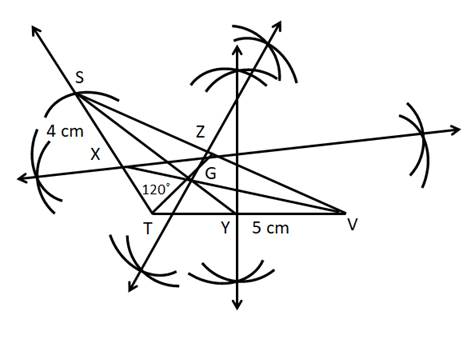
1. Draw an obtuse angled ∆ STV.
2. Draw perpendicular bisector of seg ST, seg TV and Seg SV and name their midpoints such as X, Y, Z respectively.
3. Join SY, TZ and VX which are the respective medians.
4. Name the point intersection of these lines as G.
Solution 4
Steps of constructions:
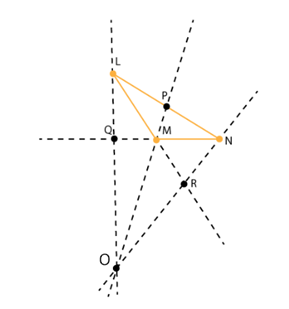
1. Draw obtuse angle ∆ LMN
2. Draw altitudes from vertex L, M, N to its opposite sides.
3. O is the point of intersection of all the altitudes. Hence, orthocentre lies in the outside region of the triangle.
Solution 5
Steps of construction:
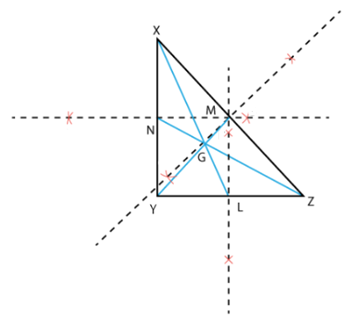
1. Draw right angled ∆ XYZ
2. Draw perpendicular bisector of seg XY, YZ and ZX.
3. Name the mid points as N, L, M respectively.
4. Join XL, YM, ZN.
5. G is the intersection point of medians.
Solution 6
Steps of Construction:
1. Draw ∆ XYZ, where XY = XZ = 4 cm and YZ = 5 cm.
2. Take vertex X by taking distance more than half of seg XY and draw a curve from vertex X and Y on the up and down side respectively. Join them which is a perpendicular bisector of seg XY.
Similarly, draw the perpendicular bisector of seg YZ and seg XZ.
3. Name the points of the midpoint of seg XY, seg XZ and seg YZ as U, K and L resepectively.
4. Join all the mid points with their opposite vertex to get the respective medians.
5. Intersection of the medians is G.
6. Draw a perpendicular from a vertex X on the side YZ using a set-square. Name the point where it meets side YZ as L.
7. Similarly, draw a perpendicular from a vertex Y on the side ZX using set-square. Name the point where it meets side ZX as M.
8. Also, perpendicular from a vertex Z to the side XY using set-square. Name the point where it meets side XY as N.
9. Name the point of concurrence of ZN, YM and XL as O.
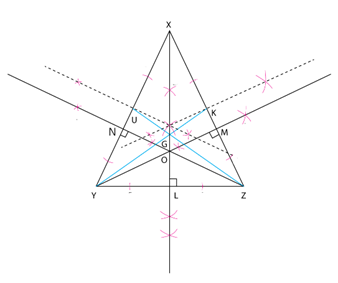
Observation:
The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line XL which is the perpendicular bisector of seg YZ
Solution 7
(1) In ∆ ABC, G is centroid
Centroid of a triangle divides the median in the ratio 2:1.
∴ RG = ![]() × GC
× GC
∴ 2.5 = ![]() × GC
× GC
∴ GC = 2 × 2.5 = 5 units
(2)
BG = ![]() × BQ
× BQ
∴ 6 =![]() × BQ
× BQ
∴ BQ = ![]() × 6 = 9 units
× 6 = 9 units
(3)
AG = ![]() × AP
× AP
∴ AG = ![]() × 6 = 4 units
× 6 = 4 units
GP = ![]() × AP =
× AP = ![]() × 6 = 2 units
× 6 = 2 units
