Class 10 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 7 - Mensuration
Mensuration Exercise 7.1
Solution 1
Given:
Radius, r = 1.5 cm
Height, h = 5 cm
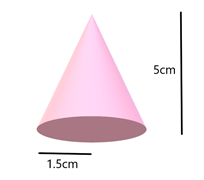
The volume of a cone

V = 𝜋 × 0.75 × 5
V = 3.75 × 3.14
V = 11.77 cm2
The volume of the cone is 11.77 cm2.
Solution 2
Given,
Diameter
of the sphere, ![]()

Therefore, radius (r)
![]()
r = 3 cm
Volume of sphere
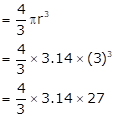
= 113.04 cm3
Volume of sphere is 113.04 cm3
Solution 3
Given,
Radius (r) of cylinder's base is 5cm
Height (h) of the cylinder is 40cm
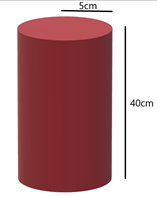
Thus,
Total surface area of the cylinder
TSA = 2𝜋rh + 2𝜋r2
TSA = 2𝜋r(h + r)
TSA = 2𝜋(5)(40 + 5)
TSA = 2𝜋(5)(45)
TSA = 2 × 3.14 × 5 × 45
TSA = 1413 cm2
The total surface area of the cylinder, TSA = 1413 cm2
Solution 4
Given;
Radius of the sphere, r=7cm

We have to find the surface area of the sphere.
SA = 4𝜋r2
![]()
SA = 616 cm2
The surface area of the sphere is 616 cm2
Solution 5
Given:
Dimensions of cuboid 44 cm × 21 cm × 12 cm
Cuboid is melted in to a cone.
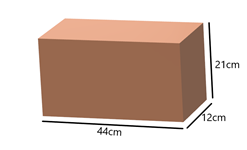
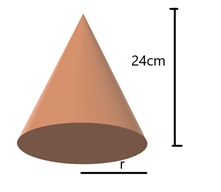
We have to radius of the cone.
Their volume will be equal thus,
Vcuboid = Vcone

r = 21 cm
The radius of the cone is 21cm.
Solution 6
Given:
Height of conical jug hc = 10cm
Radius of the conical jug rc = 3.5 cm
Height of cylindrical pot hcy = 10cm
Radius of cylindrical pot rcy = 7cm
We have to find the number of jugs of water the cylindrical pot hold.
Let the number of jugs be 'n'
Vcy = nVc

n = 12
The cylindrical pot can hold up to 12 jugs of conical jugs of water.
Solution 7
Given:
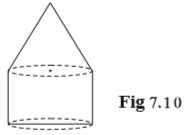
Height of the cylinder, hcy = 3 cm
Area of base, A = 100 cm2
Volume of the solid figure, Vtotal = 500 cm3= 10cm
As we can see the radii of the cone and cylinder are the same, therefore their base areas are also same.
We have to find the total height i.e., htotal = hcy + hc
Vtotal = Vcy + Vc

hc = 6 cm
htotal = hcy + hc
htotal = 3 + 6
htotal = 9cm
The total height of the solid figure is 9 cm.
Solution 8
Given,
Radius, ![]()
Height
of cone, ![]()
Height
of cylinder, ![]()
We have to find the total area of the toy.
SA = SAhemisphere+ SAcylinder + SAcone
SA = 2𝜋r2
+ 2𝜋rcy + ![]()
SA = 2𝜋32 + 2𝜋(3)(40) + 𝜋(3)√42 + 32
SA = 𝜋(18 + 240 + 15)
![]()
SA = 858 cm2
The surface area of the toy is 858 cm2
Solution 9
Given;
Radius of tablet, rt = 7mm
Thickness of tablet, t = 5mm
Radius
of wrapper, ![]()
Length of wrapper, l = 10 cm = 100 mm
We have to find the number of tablets wrapped.
Tablet:

Wrapper:

Let the number of tablets be 'n'.
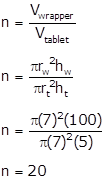
The number of tablets wrapped are 20.
Solution 10
Given:
Radius, r = 3 cm
Height of the cone, h = 4 cm
We have to find the volume and surface area.
Volume

V = 12𝜋 + 18𝜋
V = 30𝜋
V = 94.2 cm3
SA = 2𝜋r2 + 𝜋r√h2 + r2
SA = 2𝜋(3)2 + 𝜋(3)√(4)2 + (3)2
SA = 18𝜋 + 15𝜋
SA = 33𝜋
SA = 103.62 cm2
The
volume of the toy is![]() and its surface area is 103.62 cm2.
and its surface area is 103.62 cm2.
Solution 11
Given:
Diameter of ball, d = 42 cm
Radius, ![]()
We have to find the surface area and the volume of the ball.
SA = 4𝜋r2

V = 38808 cm3
The surface area of the ball is 5544 cm2 and the volume is 38808 cm3.
Solution 12
Given:
Radius
of the cylinder, ![]()
Height
of the water in the cylinder, ![]()
Diameter
of sphere, ![]()
Thus,
the radius of the sphere, ![]()
The volume of the water is

V = 4620 - 4.187
V = 4615.813 cm3.
The volume of water is 4615.813 cm3.
Mensuration Exercise 7.2
Solution 1
Given:
Radii of circular ends of frustum,
R = 14 cm
r = 7 cm
Height of the bucket, H = 30 cm
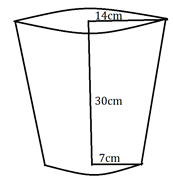
We have to find the volume(V) of water (in liters) it can hold.
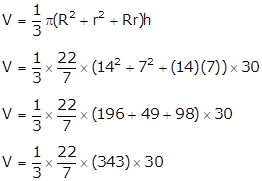
V = 10780 cm3
Volume of water
![]()
V = 10.780 Liters
The bucket can hold 10.78L in the bucket.
Solution 2
Given:
Radii of circular ends of frustum,
r = 14 cm
r = 6 cm
Height of the bucket, H = 6 cm

We have to find
(i) Curved surface area
(ii) Total surface area
(iii) Volume
The slant height (L),

L = 10 cm
(i)Curves surface area
CSA = 𝜋L(R + r)
CSA = (3.14)(10)(14 + 6)
CSA = (3.14)(10)(20)
CSA = 628 cm2
(ii) Total surface area
TSA = 𝜋(L(R + r) + (R2 + r2))
TSA = 3.14()10)(14 + 6) + (142 + 62))
TSA = 3.14(200 + 232)
TSA = 3.14(432)
TSA = 1356.48cm2
(iii) Volume
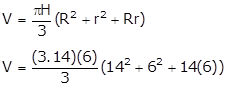
V = 2(3.14)(232 + 84)
V = 1984.48 cm3
The curved surface area, total surface area, and volume are
CSA = 628 cm2, TSA = 1356.48 cm2 and V = 1984.48 cm2 respectively.
Solution 3
Circumference (Let radius be r1) = 132 cm
2𝜋r1 = 132
![]()
r1 = 21 cm
Circumference (Let radius be r2) = 88 cm
2𝜋r2 = 88
![]()
r2 = 14 cm
Height of frustum, H = 24 cm

Therefore, slant height (L)
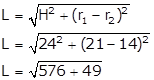
L = √625
L = 25 cm
The curved surface area is
CSA = 𝜋L(r1 + r2)
CSA = (3.14)(25)(21 + 14)
CSA = 2669 cm2
Mensuration Exercise 7.3
Solution 1
Given the radius of the circle is 10cm
The measure of the arc is 54°

We have to find the area of sector associated with the arc

A = 47.1 cm2
The area of the sector is A = 47.1 cm2
Solution 2
Given;
Radius, r = 18 cm
Measure of arc θ= 80°
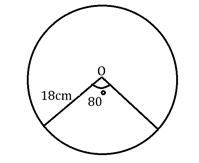
We have to find the length of the arc (L)
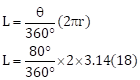
L = 25.12 cm
The length of the arc is 25.12cm.
Solution 3
Given,
Radius, r = 3.5 cm
Length of the arc AB is 2.2cm
We have to find the area of the circle (A)
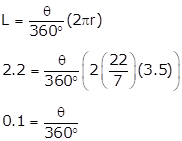
Θ = 36°
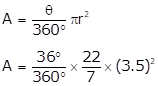
A = 3.85 cm2
The area of the sector OAB is A = 3.85 cm2
Solution 4
Given:
Radius, r = 10 cm
Area of the sector A = 100 cm2
We have to find the area of the major sector
Amajor = Acircle - Aminor
![]()
Amajor = 3.14(10)2 - 100
Amajor = 314 - 100
Amajor = 214 cm2
The area of its corresponding major sector is 214 cm2.
Solution 5
Given;
Radius of circle, r = 15 cm
Area of sector is =30 cm2

We have to find the length of the arc (L)

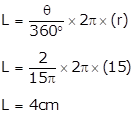
The length of the arc is 4 cm.
Solution 6
Given:
Radius, r = 7 cm
M(arc MON) = 60°

We have to find
(1) Area of circle
(2) A(OMBN)
(3) A(OMCN)
A = 𝜋r2
![]()
A =184 cm2
A(OMBN)
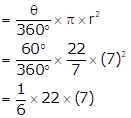
= 30.66 cm2
A(OMCN)
=A - A(OMBN)
= 184 - 30.66
= 153.33cm2
(1) Area of the circle (A), A = 184 cm2
(2) A(OMBN) = 30.66 cm2
(3) A(OMCN) = 153.33 cm2
Solution 7
Given:
Radius of the circle, r = 3.4cm
Perimeter PBAC = 12.8cm
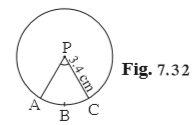
We have to find A(PABC)

θ=215.81°

A(PABC) = 21.76 cm2
Area of the sector PABC is A(PABC) = 21.76 cm2.
Solution 8
Given:

∠ROQ = ∠MON = 60°
OR = 7 cm
OM = 21 cm
We have to find lengths of arc RXQ and arc MYN
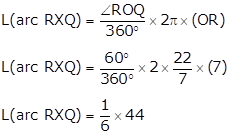
L(arc RXQ) = 7.33 cm
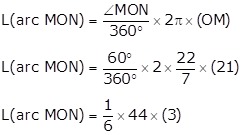
L(arc MON) = 22 cm
The lengths of the arcs are
L(arc RXQ) = 7.33 cm
L(arc MON) = 22 cm
Solution 9
Given:
A(P - ABC) = 154 cm2
Radius, r = 14cm
We have to find:
(1) ∠APC (2) l(arc ABC)
A(P - ABC) = 154 cm2

Θ =90°
Therefore, ∠APC = 90°
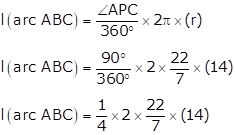
L(arc ABC) = 154 cm
Answer: (1) ∠APC = 90° (2) l(arc ABC) = 154 cm.
Solution 10
Given:
Radius, r = 7 cm
We have to find the area with measure of the arc is
(1)30° (2) 210° (3) Three right angles (270°)
(1)
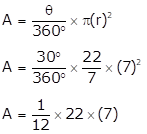
A = 12.83 cm2
(2)
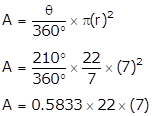
A = 89.83 cm2
(3)
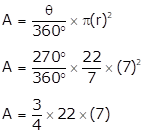
A = 115 cm2
(1) 30°, A = 12.83 cm2
(2) 210°, A = 89.83 cm2
(3) Right angles (90°), A = 115.5 cm2
Solution 11
Given:
Area of a minor sector, A = 3.85 cm2
Central angle θ = 36°
We have to find the radius of the circle
A = 3.85 cm2
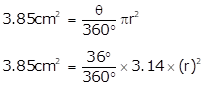
(r)2 = 7.33
r = 2.21 cm
The radius of the circle is 2.21cm.
Solution 12
Given;
▭ PQRS is a rectangle
PQ = 14 cm
QR = 21 cm

We have to find the area x, y and z

x = 154 cm2

y = 38.5 cm2
z = A(▭ PQRS) - x - y
z = (14 × 21) - 154 - 38.5
z = 101.5cm2
The area are: x = 154 cm2 y = 38.5 cm2, z = 101.5 cm2.
Solution 13
Given:
ΔLMN is an equilateral triangle
LM = 14 cm
Radius, r = 7 cm

We have to find:
(1) A(ΔLMN)
(2) Area of any one of the sectors.
(3) Total area of all the three sectors.
(4) Area of the shaded region.
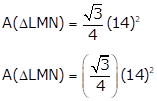
A(ΔLMN) = 84.87 cm2
Area of any one of the sectors
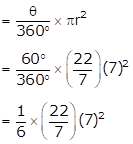
= 25.66 cm2
Total area of all the three sectors
= 3 × Area(sector)
= 3 × 25.66
= 77 cm2
Area of the shaded region
= A(Δ LMN) - 3A(sector)
= 84.87 - 77
= 7.87 cm2
Answer:
(1) A(ΔLMN) = 84.87 cm2
(2) Area of any one of the sectors = 25.66 cm2
(3) Total area of all the three sectors = 77 cm2
(4) Area of the shaded region = 7.87 cm2
Mensuration Exercise 7.4
Solution 1
Given:
∠ABC = 45°
AC = 7√2 cm
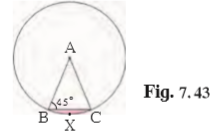
We have to the area of segment BXC
As, AB = AC = r
∠ABC = ∠ACB = 45°
In ΔABC,
∠ABC + ∠ACB + ∠BAC = 180°
45° + 45° + ∠BAC = 180°
∠BAC = 90°
Area of segment BXC (Asegment)
Asegment = Asector- AΔABC

Asegment = 28 cm2
The area of segment BXC is Asegment = 28cm2.
Solution 2
Given:
M(arc PQR) = 60°
OP = 10 cm

We have to find the area of the shaded region.
A = A(sector OPQR) - A(ΔPQR)

A=52.33 - 25(1.73)
A=9.08cm2
The area of the shaded region is A = 9.08 cm2.
Solution 3
Given:
∠PAR = 30°,
AP = 7.5

We have to find the area of the segment PQR.
A = A(sector APQR) - A(ΔAPR)
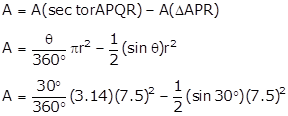
A = 14.718 - 14.0625
A = 0.655 units2
The area of the segment PQR A = 0.655 units2.
Solution 4
Given:
∠POQ = 90°
Area of shaded region = 114 cm2

We have to find the radius.
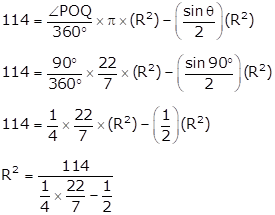
R2 = 400
R = 20 cm
The radius of the circle is 20cm.
Solution 5
Given:
Radius, r = 15cm
The angle subtended at the centre, θ=60°
We have to find the area of the minor and major segment
Area of minor segment
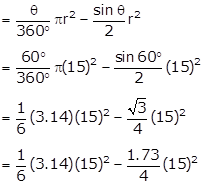
= 117.75 - 97.3125
= 20.4375 cm2
Area of major arc
= A(circle) - A(min or arc)
= 𝜋r2 - 20.4375
= (3.14)(15)2 - 20.4375
= 706 - 20.4375
= 686.0625 cm2
Area of minor segment = 20.4375 cm2
Area of major arc = 868.0625 cm2
Mensuration Exercise Problem Set 7
Solution 1(1)
Given ratio
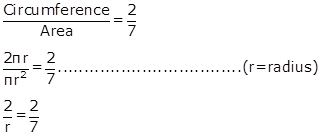
r = 7 units
Thus,
Circumference of the circle
2𝜋r
= 2 × 𝜋 × 7
= 14 𝜋units
(A) 14𝜋
Solution 1(2)
Given:
m(arc)= 160°
L(arc) = 44cm
L(arc) = 44
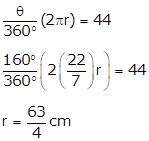
Circumference
= 2𝜋r
![]()
= 99 cm
Option (D) 99cm
Solution 1(3)
Given:
Θ = 90°
R = 7 cm
Perimeter of sector
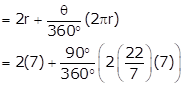
= 14 + 11
= 25 cm
Option (B) 25cm
Solution 1(4)
Given:
h = 24cm
r = 7cm
CSA = 𝜋rl
![]()
CSA = 22(25)
CSA = 550 cm2
Option (B) 550 cm2
Solution 1(5)
Given:
CSA=440cm2
R=5cm
CSA = 440
2𝜋rh = 440
2𝜋(5)(H) = 440
![]()
Option
(A) ![]()
Solution 1(6)
Vcone = Vcylinder
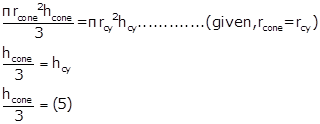
Hcone = 15 cm
Height of cone is 15cm.
Option (A) 15cm
Solution 1(7)
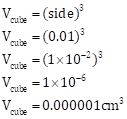
Vcube = (side)3
Vcube = (0.01)3
Vcube = (1 × 10-2)3
Vcube = (1 × 10-6
Vcube = 0.000001 cm3
Volume of cube is 0.000001 cm3
Option (D) 0.000001 cm3
Solution 1(8)
Vcube = (a)3
1 = (a)3
a = 1m
a = 100 cm
The side of cube is 100 cm
Option (C) 100 cm.
Solution 2
Given:
Height, h=21cm
Radius of top and bottom,
rt = 20 cm
rb = 15 cm
We have to find the capacity of the tub i.e., volume (in L)

V = 22(400 + 225 + 300)
V = 20350 cm3
V = 20.35 Litre
The capacity of the tub is 20.35 litre.
Solution 3
Given:
Radius of plastic balls, R = 1 cm
Thickness of tube, t=2cm
Length of tube, l=90cm
Outer radius of tube, r0 = 30 cm
Therefore, the inner radius, ri= 28 cm
The volume of the balls will be equal to the volume of the tube.
Let the number of plastic balls melted, be 'n'.
Vballs = Vtube
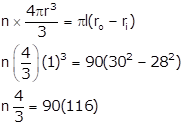
n = 7830
7830 balls were melted to make the tube.
Solution 4
Given
Dimensions of metal parallel piped =l × b× h= 16 cm × 11cm × 10 cm
Thickness of coins, T=2mm=0.2cm
Diameter of coin, D=2cm
Therefore, the radius of coin, R=1cm
The volume of the metal will be volume of the coins.
Let the number of coins be 'N'
Vmetal = Vcoins
l × b × h = N × 𝜋R2T
![]()
N = 2800
The number of coins formed will be 2800.
Solution 5
Given;
Diameter of roller, d=120cm
Length of the roller, l=84cm
Rotations required, n=200
We have to find the expenditure at the rate of Rs. 10 per m2
To find the expenditure we have to find the area covered by the roller
A = n × 𝜋dl
![]()
A = 6336000 cm2
A = 633.6 m2
Expenditure
= A × rate
= 633.6 × 10
= Rs. 6336
The expenditure to level the ground is Rs. 6336.
Solution 6
Given;
Diameter of hollow sphere, d=12cm
Radius, r=6cm
Thickness, t=0.01m=1cm
Density, δ = 8.88gm/cm3
We have to find the outer surface area and mass of the hollow sphere
Surface area
= 4𝜋r2
= 4(3.14)(6)2
= 452.16 cm2
Mass

= 3383.16g
The outer surface area is 452.16cm2 and mass is 3383.16g of the hollow sphere.
Solution 7
Given;
Diameter of cylindrical bucket, d=28cm
The radius of the cylindrical bucket, r=14cm
Height of cylindrical bucket, h=20cm
Height of the cone, H=14cm
We have to find the base area of the cone
The volume of sand will remain the same therefore,
Vcy = Vcone
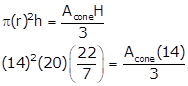
Acone = 2640 cm2
The base area of the cone is 2640 cm2.
Solution 8
Given:
Radius of sphere, R=9cm
Diameter of wire, d=4mm
Radius of wire, r=1mm=0.2cm
We have to find length of wire
Vsphere = Vwire
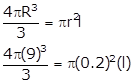
l = 24300 cm
l = 243m
The length of the wire is 243m.
Solution 9
Given:
Radius of circle, r=6cm
Area of sector, A=15π sq.cm
We have to find measure of the arc, and length of the arc (L).
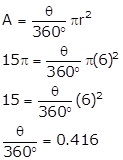
θ = 150°
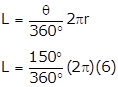
L = 5𝜋cm
The measure of the arc is 150°, and length of the arc is 5𝜋cm.
Solution 11
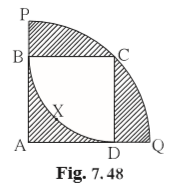
Side of square ABCD = radius of sector C-BXD = 20cm
Area of square = (side)2 = 202 = 400 cm2
Area of shaded region inside the square
= Area of square ABCD - Area of sector C-BXD
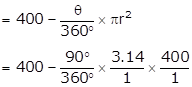
= 400 - 314
= 86 cm2
Radius of bigger sector = Length of diagonal of square ABCD
= 20√2
Area of the shaded regions outside the square
= Area of sector A-PCQ - Area of square ABCD
=A(A - PCQ) - A(▭ABCD)
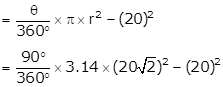
= 628 - 400
= 228 cm2
![]() total area of the shaded region =
86 + 228 = 314 cm2.
total area of the shaded region =
86 + 228 = 314 cm2.
Solution 12
Let the radius of the bigger circle be R and that of smaller circle r.

OA, OB, OC and OD are the radii of the bigger circle
∴ OA = OB = OC = OD = R
PQ = PA = R
OQ = OB - BQ = (R - 9)
OE = OD - DE = (R - 5)
As the chords QA and EF of the circles with centre P intersect in the interior of the circle, so by the property of internal division of two chords of a circle,
OQ × OA = OE × OF
(R - 9) × 9 = (R - 5) × (R - 5)………(∵ OE = OF)
R2 - 9R = R2 - 10R + 25
R = 25 cm
AQ = 2r = AB - BQ
2r = 50 - 9 = 41
![]()
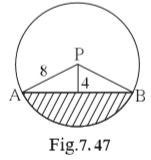
Solution 10
Given:
PA=8cm
PM=4cm
![]()
θ 60°
m(arc AB) = 2θ = 120°
In ΔPAM,
82 = 42 + (AM)2
64 = 16 + (AM)2
In ΔPAM,
82 = 42 + (AM)2
64 = 16 + (AM)2
![]()
AM = √48
AM = 4√3 cm
∴ AB = 2 AM
AB = 8√3 cm
Area of shaded portion
= A(sector) - A(Δ PAB)
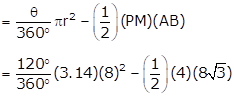
= 66.986 - 27.712
= 39.271 cm2
The area of the shaded region is 39.272 cm2.

