Class 10 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 3 - Circle
Circle Exercise 3.1
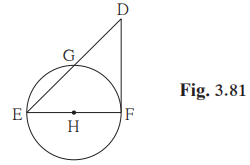
Solution 1
Given:
Radius = 6cm
AB is tangent to the circle
(1)
Measure of 
As AB is tangent to the circle, therefore the radius CA is perpendicular to AB.
(2) Distance of C from AB
Point A is on the circle as the line AB is tangent, therefore CA=radius=6cm.
(3) d(A,B)=6cm, d(B,C)
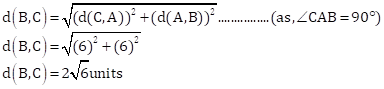
(4) The measure of ∠ABC
Solution 2
Given:
RM and RN are tangents
OR=10cm
Radius=5cm
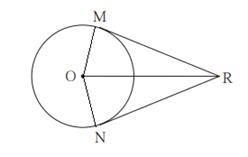
(1) Length of segments RM and RN
(2) Measure of ∠MRO
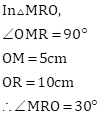
(3) Measure of ∠MRN
Solution 3
Given:
RM and RN are tangents
In
RM=RN………………(tangents from the same point)
OM=ON………………….(radii of circle)
OR is common side
By SSS rule,
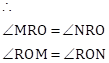
Hence proved OR bisects ∠MRN and ∠MON.
Solution 4
Given:
Radius, r=4.5cm
Tangents AM and BN are parallel to each other
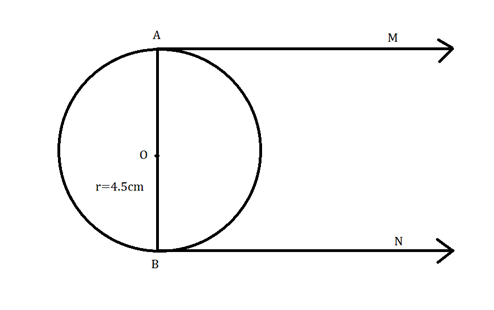
As AM is the tangent to the circle
∠OAM=90°
And as BN is the tangent to the circle
∠OBN=90°
Thus AB is a straight line passing from O.
AB is the diameter of the circle.
Therefore,
AB=2r
AB=9cm
Thus, the distance between the two parallel tangents is 9 cm.
Circle Exercise 3.2
Solution 1
Given:
The circle touch internally
We have to find the distance between the centres, A and B i.e., d
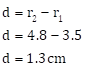
The distance between the centres is 1.3cm.
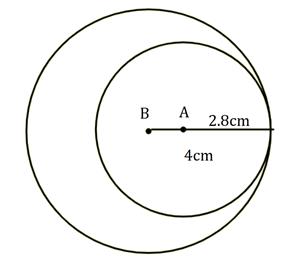
Solution 2
Given:
Distance between centres,
= r1 + r2
= 5.5 + 4.2
= 9.7 cm
The distance between the centres is 9.7cm.
Solution 3
Given:
Radius of circle,
We have to draw circles touching each other (tangent to each other)
(1) Externally
(2) Internally
Solution 4
Given:
Circles are tangent to each other
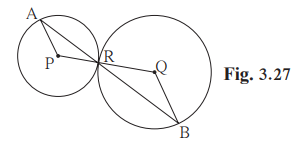
P-R-Q are collinear points, as radii meet at the tangent point R.
We have to show,
(1) seg AP || seg BQ
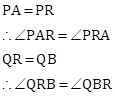
As,
…………………(vertically
opposite angles)
(2) ΔAPR ~ ΔRQB
By AA similarity test,
(3) ∠RQB if ∠PAR = 35°
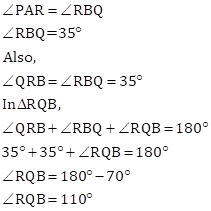
Solution 5
Given:
Circles with centre A and B touch each other at E,
Line l is a common tangent, at C and D
Radii,
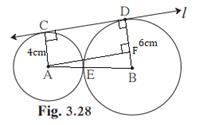
From the above figure,
is a rectangle
AC=DF=4cm
Measure of segment CD is 
.
Circle Exercise 3.3
Solution 1
Given:
G, D, E, F are concyclic points
∠ECF = 70°
m(arc DGF) = 200°
We have to find:
m(arc DE) and m(arc DEF)
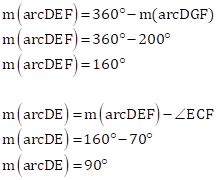
Thus,
and 
.
Solution 2
Given:
ΔQRS is an equilateral triangle
We have to prove
(1) arc RS ≅ arc QS ≅ arc QR
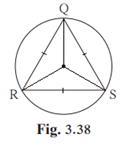
As,
Therefore, arc RS ≅ arc QS ≅ arc QR
As chords of corresponding arcs are equal because it is a equilateral triangle the arcs are congruent.
(2) m(arc QRS) = 240°.
In
,
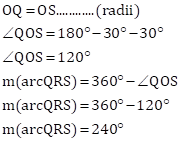
Solution 3
Given:
chord AB ≅ chord CD
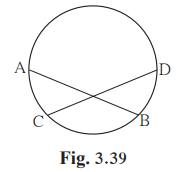
We have to prove that arc AC ≅ arc BD
chord AB ≅ chord CD
∴ arc (AB)=arc (CD)…………… (corresponding chords are equal)
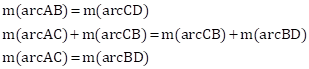
Circle Exercise 3.4
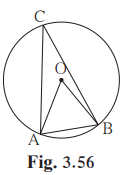
Solution 1
Given:
AB=radius of the circle
We have to find measures of
(1) ∠AOB (2)∠ACB (3) arc AB (4) arc ACB.
(1) ∠AOB
As,
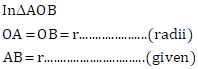
is an
equilateral triangle
(2) ∠ACB
(3) m(arcAB)
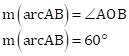
(4) m(arcACB)
Solution 2
Given:
▭ PQRS is cyclic
side PQ ≅ side RQ
∠PSR = 110°
(1) ∠PQR
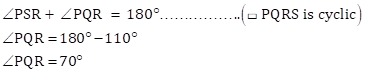
(2) m(arcPQR)
According to Inscribed angle theorem
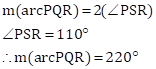
(3) m(arc QR)
(4) measure of ∠PRQ
Solution 3
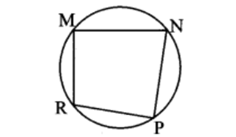
Given:
▭ MRPN is cyclic,
∠R = (5x - 13)°,
∠N=(4x+4)°
Solution 4
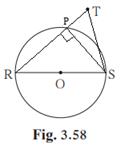
Given:
seg RS is a diameter of the circle with centre O
Point T lies in the exterior of the circle
Construction:
Join RT. RT is intersecting circle at P
Join RP, PS and TS
As, RS is the diameter
'………………..(Diameter
subtends right angle on the circle)
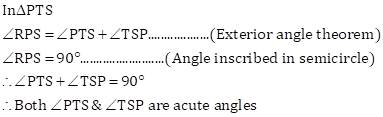
Solution 5
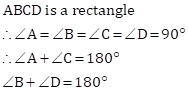
Hence proved, any rectangle is a cyclic quadrilateral.
Solution 6
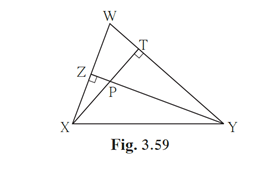
Given:
YZ and XT are altitudes of ΔWXY
YZ and XT intersect at P
To prove that:
(1) ▭ WZPT is cyclic.
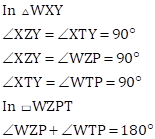
Therefore, WZPT is a cyclic quadrilateral.
(2) Points X, Z, T, Y are concyclic
Line
XY subtends 
As, line XY subtend equal angles at two distinct points T and Z which lie on the same side of the line XY, the four points X, Z, T and Y are concyclic.
Solution 7
Given:
m(arc NS) = 125°
m(arc EF) = 37°
To find:
∠NMS
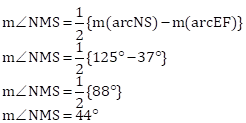
The
measure of ∠NMS is 
.
Solution 8
Given:
Chords AC and DE intersect at B
∠ABE = 108°,
m(arc AE) = 95°
To find:
m(arc DC)
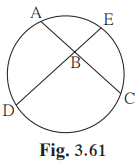
Two chords AC and DE of a circle intersect each other in the interior at point B. Hence,
Circle Exercise 3.5
Solution 1
Given:
PQ touches the circle at point Q
PQ=12cm
PR=8cm
We have to find
PS and RS
Using the tangent secant theorem
The sides PS=18cm and RS=10cm.
Solution 2
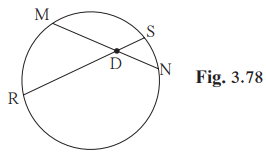
Given:
Chord MN and chord RS intersect at point D
(1) If RD = 15, DS = 4, MD = 8
To find: DN
Using the internal division of chords theorem,
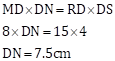
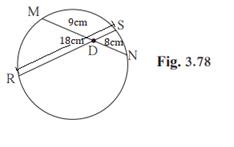
(2) If RS = 18, MD = 9, DN = 8
To find: DS
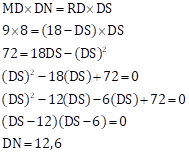
DN=12cm or DN=6cm.
Solution 3
Given:
O is the centre of the circle
B is a point of contact
seg OE ⊥ seg AD
AB = 12
AC = 8
To find:
(1) AD
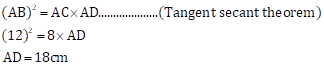
(2) DC
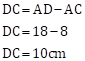
(3) DE
As, perpendicular from the centre bisects the chord.
OE is perpendicular to chord DC,
Therefore,
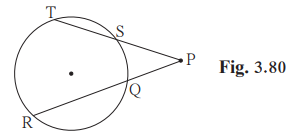
Solution 4
Given:
PQ = 6,
QR = 10,
PS = 8
To find:
TS
According to external intersection of chord theorem,
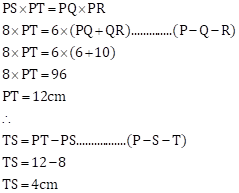
Solution 5
Given:
Seg EF is a diameter
Seg DF is a tangent segment
The radius of the circle is r
To prove that:
DE × GE = 4r2
Hence proved.
Circle Exercise Problem Set 3
Solution 1(1)
Given that two circles with 5.5cm and 3.3cm touch
Circles can touch internally or externally
Condition 1: If the circles touch externally,
Distance between centres
=5.5cm+3.3cm
=8.8cm
Condition 2: If the circles touch internally,
Distance between centres
=5.5cm-3.3cm
=2.2cm
Answer: (D) 8.8cm or 2.2.cm
Solution 1(2)
Given:
Distance between centres = 12cm
Circles intersect each other such that each circle passes through the centre of the other
To find:
Radius of each circle
As, each circle passes through the centre of each other,
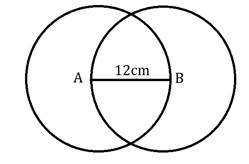
Consider the two circles with centres A and B
As we can see the radius of both the circles are equal
Thus the radius of each circle is
=12cm
Answer: (B) 12cm
Solution 1(3)
A circle touches all sides of a parallelogram. So the parallelogram must be a, rectangle.
Answer: (B) rhombus
Solution 1(4)
Given:
Point (say P) is at a distance 12.5 cm from the centre of the circle (say O)
Length of a tangent (PQ) drawn from that point is 12cm
To find:
The diameter of the circle
Consider the diagram
Join the centre with the point of tangent
OQ ⊥ PQ
OQ = radius
In Δ PQO
(12.5)2 = 122 + (OQ)2
(OQ)2 = 12.25
OQ = 3.5 cm
Therefore,
Diameter of the circle
= 2 × 3.5
= 7 cm
Answer: (C) 7cm
Solution 1(5)
Two circles touch externally, the number of common tangents that can be drawn are two.
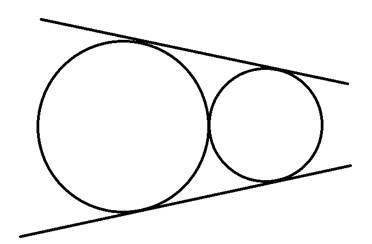
Answer: (B) Two
Solution 1(6)
Given:
∠ACB is inscribed in arc ACB of a circle with centre O
∠ACB = 65°
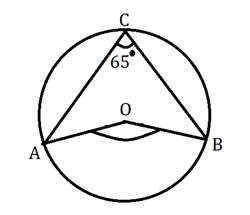
To find:
m(arc ACB) = 360° - m(∠AOB)
m(arc ACB) = 360° - 2 × m(∠ACB)
m(arc ACB) = 360° - 2 × 65°
m(arc ACB) = 360° - 130°
m(arc ACB) = 230°
Answer: (D) 230°
Solution 1(7)
Given:
Chords AB and CD of a circle intersect inside the circle at point E
AE = 5.6,
EB = 10,
CE = 8
To find:
ED
According to the internal intersection of chords theorem
AE × EB = CE × ED
5.6 × 10 = 8 × ED
ED = 7
Answer: (A) 7
Solution 1(8)
Given:
▭ABCD is a cyclic quadrilateral
twice the measure of ∠A is thrice the measure of ∠C i.e., 2m∠A = 3m∠C
To find:
m∠C
m∠A + m∠C = 180°……..(cyclic quadrilateral)
(m∠C) + m∠C
= 180°……..(from (1))
m∠C = 72°
Answer: (B) 72
Solution 1(9)
Given:
Points A, B, C are on a circle
m(arc AB) = m(arc BC) = 120°
No point, except point B, is common to the arcs
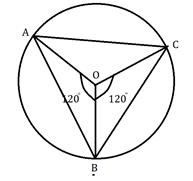
To find:
Δ ABC
m(arc AB) = m(arc BC) = 120°
∴ m(arc AC) = 360° - m(arc AB) - m(arc BC)
m(arc AC) = 120°
∴ AB = BC = CA………(corresponding chords of congruent arcs)
ΔABC is an equilateral triangle
Answer: (A) Equilateral triangle
Solution 1(10)
Given:
Seg XZ is a diameter of a circle
Point Y lies in its interior
Statements:
(i) It is not possible that ∠XYZ is an acute angle.
True
(ii) ∠XYZ can't be a right angle.
True
(iii) ∠XYZ is an obtuse angle.
True
(iv) Can't make a definite statement for measure of ∠XYZ.
False
Answer: (C) Only three
Solution 2
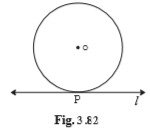
Given:
The radius of the circle is, r=9 cm
Line l touches a circle with centre O at point P
(1) d(O, P)
d(O, P) = r
d(O, P) = 9 cm
OP is the radius of the circle.
(2) If d(O, Q) = 8 cm, where does the point Q lie?
d(O, Q) = 8 cm
d(O, Q) < d(O, P)……(As, 8 < 9)
Q lies inside the circle.
(3) If d(OR) = 15 cm, How many locations of point R are line on line l ? At what distance will each of them be from point P?
In Δ OPR
(OR)2 = (OP)2 + (PR)2
152 = 92 + (PR)2
PR = √144
PR = 12 cm
R is at a distance of 12cm from P.
Solution 3
Given:
M is the centre of the circle
Seg KL is a tangent segment
MK = 12,
KL = 6√3
(1) Radius of the circle.
In Δ MLK
(MK)2 = (ML)2 + (LK)2………(∠L = 90°)
(12)2 = (ML)2 + (6√3)2
ML = √144 - 108
ML = 6cm
(2) Measures of ∠K and ∠M.
∴ ∠K = 30°
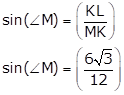
∴ ∠K = 60°
Solution 4
Given:
O is the centre of the circle
Seg AB, seg AC are tangent segments
Radius of the circle is r
and l(AB) = r
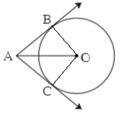
To prove that:
▭ ABOC is a square
AB = AC…….(Tangent segments from the same external point)
OB = OC = r……(radii)
AB = r……(given)
AB = AC = OB = OC
∴ ▭ABOC is a square
Hence proved.
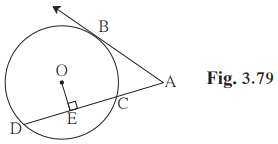
Solution 5
Given:
▭ ABCD is a parallelogram, circumscribes the circle with centre T
Point E, F, G, H are touching points
AE = 4.5,
EB = 5.5
To find:
AD
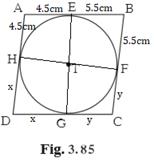
Tangent segments from the same point are equal,
∴ AE = AH = 4.5 cm
DG = DH = x
CG = CF = y
BE = BF = 5.5cm
AB = CD
and AD = BC……(ABCD is a parallelogram)
∴ CD = AB = 4.5 + 5.5
x + y = 10…….(1)
AD = BC
x + 4.5 = y + 5.5
x - y = 1……..(2)
∴ x = 5.5 cm
y = 4.5 cm……(from (1) and (2))
AD = 4.5 + x
AD = 10 cm
Solution 6
Given:
The circle with centre M touches the circle with centre N at point T
Radius RM touches the smaller circle at S
Radii of circles are R = 9 cm and r = 2.5 cm
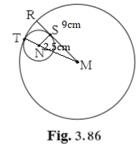
(1) Find the length of segment MT
MT = R
MT = 9cm
(2) Find the length of seg MN
MN = MT - NT
MN = R - r
MN = 9 - 2.5
MN = 6.5 cm
(3) Find the measure of ∠NSM.
As, MR touches smaller circle at point S,
Therefore, MR ⊥ NS
∠NSM = 90°
The ratio MS : SR
In Δ MSN,
(MN)2 = (NS)2 + (MS)2
(6.5)2 = (2.5)2 + (MS)2
(MS)2 = 36
MS = 6cm
MS : SR = 2 : 1
Solution 7
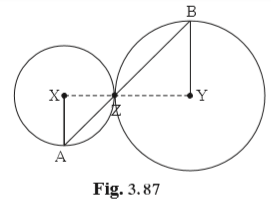
Construction: Draw segments XZ and YZ
Proof: By theorem of touching circles, points X, Z, Y are collinear.
∴ ∠XZA ≅ ∠YZB opposite angles
Let ∠XZA = ∠BZY = a ..... (I)
Now, seg XA ≅ seg XZ ........ (radii of the same circle)
∴ ∠XAZ =∠YBZ = a ........ (Isosceles triangle theorem) (II)
similarly, seg YB ≅ seg YZ ........(radii of the same circle)
∴ ∠BZY =∠YBZ = a ........ (Isosceles triangle theorem) (III)
∴ from (I), (II), (III), ∠XAZ = ∠YBZ .............( from (II)and(III) )
∴ radius XA || radius YB .......... (Alternate angles of parallel lines)
Solution 8
Given: Circles with centres X and Y touch internally at point Z
Construction: Join XZ and YZ
In ΔBYZ
Seg BY = seg ZY…………………...(radii of circle with centre Y)
YBZ=YZB……………..(base angles of Isosceles ΔBYZ)……..(1)
In ΔAXZ
Seg AX =seg ZX…………………..(radii of circle with centre X)
XAZ=XZA……………..(base angles of Isosceles Δ AXZ)………(2)
YZB=XZA……………(Z-X-Y and same angle with different name)……(3)
XAZ=YBZ……………(from (1),(2) and (3))
seg AX || seg BY………(corresponding angle test)
Solution 9
Given: line l touches the circle with centre O at point P
Q is the mid-point of radius OP.
RS is a chord through Q such that chords RS || line l.
RS = 12
To find Radius of the circle
Construction: Join OR
Seg OP ⊥ l…………..( line l touches the circle with centre O at point P)
seg OP ⊥ seg RS………….. (chords RS || line l)
seg RQ=seg QS……………….(⊥ drawn from centre bisects the chord)
RQ=
RQ=6…………………..(RS=12)
let OP=x
OQ=
…………….Q is mid point of OP
OP= OR=x…………….(radii of same circle)
In Δ OQR
OR2 = OQ2 + OR2……..….(Pythagoras theorem)
∴ x = 4√3
OR=x=4√3
Radius is equal to 4√3
Hence proved.
Solution 10
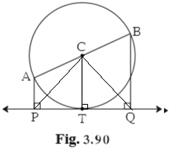
Given:
AB is the diameter of the circle with centre C
Line PQ is a tangent, which touches the circle at point T
seg AP ⊥ line PQ
and seg BQ ⊥ line PQ
To prove that:
seg CP ≅ seg CQ
As, PQ is tangent to the circle at point T
CT ⊥ PQ
Given that seg AP ⊥ line PQ and seg BQ ⊥ line PQ
∴ AP ∥ CT ∥ BQ
In ΔCTP and ΔCTQ,
TQ = PT
∠CTP = ∠CTQ = 90°
CT is common
∴ by SAS congruency test,
ΔCTP ≅ ΔCTQ
∴ seg CP ≅ seg CQ
Hence proved.
Solution 11
Construction:
1. Draw an equilateral triangle ABC with side equal to 6cm.
2. Draw mid points P, Q and R on AB, BC and AC respectively.
3. Draw circles with radius equal to 3cm as A, B and C centres.
As we can see each circle touches the other two circles at points P, Q and R.
Solution 12
Construction:
1. Draw a circle and take any three points A, B and C on the circle
2. Draw perpendicular bisectors of sides AB and BC
For A, B and C to be collinear the bisectors of AB and BC will be parallel…..(1)
OA=OB=OC
Perpendicular drawn from the centre to chord, bisects the chord….(theorem)…(2)
Thus,
Perpendicular bisectors of chord AB and chord BC meet at O.
Therefore, A, B and C are not collinear……………(from (1) and (2))
Hence proved.
Solution 13
Given:
Line PR touches the circle at point Q
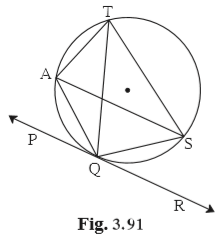
(1) The sum of ∠TAQ and ∠TSQ
▭ASTQ is a cyclic quadrilateral
∴ ∠TAQ + ∠TSQ = 180°
(2) The angles which are congruent to ∠AQP.
∠APQ ≅ ∠ATQ
∠APQ ≅ ∠ASQ……..(Angle subtended by the same arc)
(3) Angles congruent to ∠QTS
∠QTS ≅ ∠QAS…..(Angle subtended by the same arc QS)
(4) Given, ∠TAS = 65°, the measure of ∠TQS and arc TS.
∠TAS = 65°
∠TQS = ∠TAS……(Angle subtended by the same arc TS)
∴ ∠TQS = 65°
m(arc TS) = 2m (∠TAS)
m(arc TS) = 2(65°)
∴ m(arc TS) = 130°
(5) If ∠AQP = 42°and ∠SQR = 58°, the measure of ∠ATS.
∠AQP = 42°
∠SQR = 58°
∠AQP = ∠ATQ = 42°……….(Angle subtended by the same arc)
∠SQR = ∠STQ = 58°……….(Angle subtended by the same arc)
∠ATS = ∠ATQ + ∠STQ
∠ATS = 42° + 58°
∠ATS = 100°
Solution 14
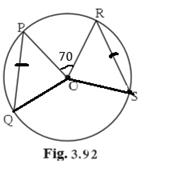
Given:
O is the centre of a circle
chord PQ ≅ chord RS
∠POR = 70° and m (arc RS) = 80°
To find:
(1) m (arc PR)
m (arc PR)=m ∠POR …………(Definition of measure of arc)
m(arc PR) = 70°
(2) m (arc QS)
chord PQ ≅ chord RS.
arc PQ ≅ arc RS………. (Arcs subtended by of congruent chords)
m ∠POQ = m ∠ROS……. (Definition of measure of arc)
m (arc RS) = 80°
m (arc PQ) = 80°
m(arc RS) + m(arc QS) + m(arc QP) + m(arc PR) = 360°…..(measure of circle)
m(arc QS) = 360° - 80° - 80° - 70°
m(arc QS) = 130°
(3) m (arc QSR)
m(arc QSR) = m (arc QS) + m (arc SR)
m(arc QSR) = 130°+80°
m(arc QSR) = 210°
Solution 15
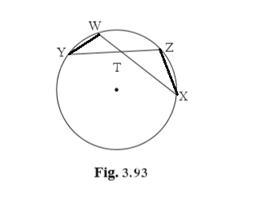
Given: m(arc WY) = 44°, m(arc ZX) = 68°
1. measure of ∠ZTX=
{m(arc WY)+m(arc ZX)}
= 56
measure of ∠ZTX=
2. find TZ
WT = 4.8, TX = 8.0, YT = 6.4
WX and YZ are chords of circle
WT × TX = YT × TZ…..(Property of internal divisions of two chords)
4.8 × 8.0 = 6.4 ×TZ
TZ = 6
3. find WT
WX = 25, YT = 8, YZ = 26
WX = WT + TX
Let WT = x
TX = WX - x
TX = 25 - x
YZ = YT + TZ
TZ = YZ - YT
TZ = 26 - 8
TZ = 18
WT × TX = YT × TZ
X(25 - x) = 8 × 18
X2 - 25x + 144 = 0
(x - 16)(x - 9) = 0
∴ x = 16 or x = 9
Therefore WT=16 or WT=9
Solution 16
(1) find measure of ∠CAE.
m(arc CE) = 54°, m(arc BD) = 23°
∴ m∠CAE = {m(arc EC) - m(arc BD)}…(chords of circle intersect each
other externally)
m∠CAE
= 
{m(arc EC) - m(arc BD)}…(
m∠CAE
= {54° - 23°}
m∠CAE = 15.5°
(2) If AB = 4.2, BC = 5.4, AE = 12.0, find AD
AB × AC = AD × AE
4.2 × (AB + BC) = AD × 12
4.2 × (4.2 + 5.4) = AD × 12
AD = 3.36
(3) If AB = 3.6, AC = 9.0, AD = 5.4, find AE
AB × AC = AD × AE
3.6 × 9 = 5.4 × AE
AE = 6
Solution 17
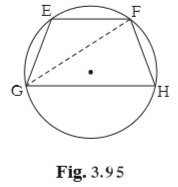
Proof: Draw seg GF.
∠EFG = ∠FGH .......... alternate angle test as, chord EF || chord GH (I)
∠EFG =
....... inscribed angle theorem (II)
∠FGH = 
....... inscribed
angle theorem (III)
∴ m(arc EG) = m(arc FH) from (I), (II), (III).
chord EG ≅ chord FH .......... corresponding chords of congruent arc are congruent
Solution 18
Given:
P is the point of contact.
(1) If m(arc PR) = 140°, ∠POR = 36°, find m(arc PQ)
m∠POR = ½ {m(arc PR) - m(arc PQ)}……..(tangent secant angle theorem)
36°=1/2{140° - m(arc PQ)}
m(arc PQ) = 140° - 72°
m(arc PQ) = 68°
(2) If OP = 7.2, OQ = 3.2, find OR and QR
OP2 = OQ × OR….(tangent secant theorem)
7.22 = 3.2 × OR
OR = 16.2
QR = OR - OQ
QR = 16.2 - 3.2
QR = 13
(3) If OP = 7.2, OR = 16.2, find QR.
OP2 = OQ × OR…(tangent secant theorem)
7.22 = 16.2 × OQ
OQ = 3.2
QR = OR - OQ
QR = 16.2 - 3.2
QR = 13
Solution 19
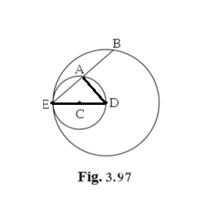
Given:
1. circles with centres C and D touch internally at point E.
2. D lies on the inner circle.
3. Chord EB of the outer circle intersects inner circle at point A.
To Prove that:
seg EA ≅ seg AB.
Proof:
Circles with centres C and D touch internally at point E……(1)
D lies on the inner circle. …..(2)
Therefore E-C-D……..(from (1)(2))
Seg ED is diameter of inner circle
∠EAC = 90°…..(angle inscribed in semicircle)
Seg DA ⊥ seg BE….(∠DAE = 90°)
D is centre of outer circle.
Seg EA ≅ seg AB…..(perpendicular drawn from centre bisects the chord)
Hence proved.
Solution 20
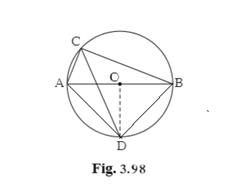
Given:
seg AB is a diameter of a circle with centre O.
The bisector of ∠ACB intersects the circle at point D.
Construction: Draw seg OD.
Proof:
∠ACB = 90° .......... angle inscribed in semicircle
∠DCB = 45° .......... CD is the bisector of ∠C
m(arc DB) = 90°.......... inscribed angle theorem
∠DOB = 90°. definition of measure of an arc (I)
seg OA ≅ seg OB .........radii of same circle. (II)
∴ line OD is perpendicular bisector of seg AB .......... From (I) and (II)
∴ seg AD ≅ seg BD
Solution 21
Given:
seg MN is a chord of a circle with centre O.
MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5.
Find the radius of the circle.
Construction:
Draw perpendicular OP on MN
Seg MP=seg PN…….(perpendicular from centre bisects the chord)
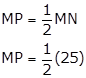
MP=12.5…………….(1)
MP=ML+LP
LP=MP-ML
LP=12.5-9
LP=3.5
In ΔOPL
OL2 = OP2 + LP2…..Pythagoras theorem
52 = OP2 + (3.5)2
OP2 = 12.75………(2)
In ΔMOP
OM2 = MP2 + OP2…… Pythagoras theorem
OM2 = (12.5)2 + (12.75)……from(1) and (2)
OM2 = 169
OM = 13
The radius of the circle is 13 units.
Solution 22
Given:
Circles intersect each other at points S and R
The common tangent PQ touches the circles at points P, Q
To prove that:
∠PRQ + ∠PSQ = 180°
∠RPQ = ∠PSR
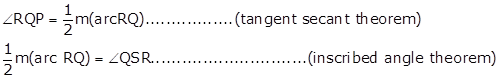
∠RQP = ∠QSR
In ΔPRQ,
∠PRQ = 180° - (∠RPQ + ∠RQP)
∠PRQ = 180° - (∠PSR + ∠QSR)
∠PRQ = 180° - ∠PSQ
∠PRQ + ∠PSQ = 180°
Hence proved.
Solution 23
Given:
The two circles intersect at points M and N
Secants drawn through M and N intersect the circles at points R, S and P, Q respectively.
To prove that:
seg SQ || seg RP.
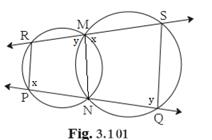
RMNP is cyclic quadrilateral
∠RPN = 180° - ∠RMN…….(cyclic quadrilateral)
∠RMN + ∠SMN = 180° ………(linear pair)
∴ ∠RPN = ∠SMN = x
SMNQ is cyclic quadrilateral
∠SQN = 180° - ∠SMN………(cyclic quadrilateral)
∠SMN + ∠RMN = 180°…….(linear pair)
∴ ∠SQN = ∠RMN = y
∵ x + y = 180°
∠RPM + ∠SQN = 180°
Interior angles of the lines RP and SQ are supplementary
Therefore,
RP ∥ SQ
Hence proved.
Solution 24
Given:
The two circles intersect each other at points A and E
The common secant through E intersects the circles at points B and D
The tangents of the circles at points B and D intersect each other at point C
To prove that:
▭ABCD is cyclic
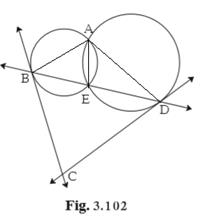
∴ ∠EBC = ∠BAE
∴ ∠EDC = ∠DAE
In ΔBCD,
∠BCD = 180° - (∠BDC + ∠DBC)…..(1)
∠BCD = 180° - (∠BAE + ∠DAE)
∠BCD = 180° - ∠BAD
Therefore, ▭ABCD is a cyclic quadrilateral.
Hence proved.
Solution 25
Given:
seg AD ⊥ side BC,
seg BE ⊥ side AC,
seg CF ⊥ side AB
Point O is the orthocentre.
To prove that:
Point O is the incentre of ΔDEF
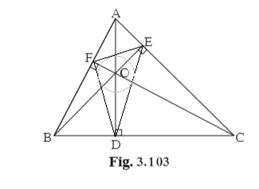
In ▭OFAE
∠OFE = 90° ………..OF ⊥ AB
∠OFE = 90° ………..OE ⊥ AC
∠OFE + ∠OEA = 180°
▭OFAE is cyclic quadrilateral
∴O, F, A and E are concyclic points.
seg OE subtends equal angles ∠OFE and ∠OAE on the same side of OE.
∴ ∠OFE = ∠OAE………..(1)
Similarly, we can prove
▭ OFBD is cyclic and O, F, B and D are concyclic points
∠OFD = ∠OBD……..(2) angle subtended by same chord OD
In ∆AEO and ∆BDO,
∠AEO = ∠BDO =90°
∠AOE = ∠BOD ……………..(Vertically opposite angles)
∴ ∆AEO ~ ∆BDO…….. (AA test of similarity)
∴ ∠OAE = ∠OBD …………….. ( Corresponding angles of similar triangles)
∴ ∠OFE = ∠OFD ……………(From (1)and(2))
∴ FO bisects ∠EFD.
Similarly, we can prove EO and DO bisects ∠FED and ∠FDE respectively.
∴ Point O is the intersection of angle bisectors of ∠D, ∠E and ∠F of ∆DEF.
∴ Point O is the incentre of ∆DEF.
