Class 10 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 2 - Quadratic Equations
Quadratic Equations Exercise Ex. 2.1
Solution 1
Quadratic equations:
x2 - 5x + 6 = 0
x2 - 9 = 0
Solution 2(i)
The given equation is x2 + 5x - 2 = 0
Here, x is the only variable and maximum index of the variable is 2.
Also, a = 1, b = 5, c = -2 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
Solution 2(ii)
The given equation is y2 = 5y - 10
∴ y2- 5y + 10 = 0
Here, y is the only variable and maximum index of the variable is 2.
Also, a = 1, b = -5, c = 10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
Solution 2(iii)
The given
equation is ![]()
Multiplying both sides by of the equation by y
∴ y3 + 1 = 2y
∴ y3- 2y + 1 = 0
Here, y is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.
Solution 2(iv)
The given equation is ![]()
Multiplying both sides by x
∴ x2 + 1 = -2x
∴ x2 + 2x+ 1 = 0
Here, x is the only variable and maximum index of the variable is 2.
Also, a = 1, b = 2, c = 1 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
Solution 2(v)
The given equation is (m + 2)(m - 5) = 0
Expanding the above equation, we get
m2 + 2m - 5m - 10 = 0
∴ m2 - 3m - 10 = 0
Here, m is the only variable and maximum index of the variable is 2.
Also, a = 1, b = -3, c = -10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
Solution 2(vi)
The given equation is m3 + 3m2 - 2 = 3m3
∴ m3 - 3m3 + 3m2 - 2 = 0
∴ -2m3 + 3m2 - 2 = 0
Here, m is the only variable and maximum index of the variable is 3.
∴ The given equation is not a quadratic equation.
Solution 3(i)
The given equation is 2y = 10 - y2
∴ y2 + 2y - 10 = 0
This is a quadratic equation.
Comparing the above equation with ay2 + by + c = 0, we get
a = 1, b = 2 and c = -10
Solution 3(ii)
The given equation is (x - 1)2 = 2x + 3
∴ x2 - 2x + 1 = 2x + 3
∴ x2 - 2x + 1 - 2x - 3 = 0
∴ x2 - 4x - 2 = 0
This is a quadratic equation.
Comparing the above equation with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = -2
Solution 3(iii)
The given equation is x2 + 5x = -(3 - x)
∴ x2 + 5x + (3 - x) = 0
∴ x2 + 4x + 3 = 0
This is a quadratic equation.
Comparing the above equation with ax2 + bx + c = 0, we get
a = 1, b = 4 and c = 3
Solution 3(iv)
The given equation is 3m2 = 2m2 - 9
∴ 3m2 - 2m2 + 9 = 0
∴ m2 + 9 = 0
This is a quadratic equation.
Comparing the above equation with am2 + bm + c = 0, we get
a = 1, b = 0 and c = 9
Solution 3(v)
The given equation is p(3 + 6p) = -5
∴ 3p + 6p2 + 5 = 0
∴ 6p2 + 3p + 5 = 0
This is a quadratic equation.
Comparing the above equation with ap2 + bp + c = 0, we get
a = 6, b = 3 and c = 5
Solution 3(vi)
The given equation is x2 - 9 = 13
∴ x2 - 9 - 13 = 0
∴ x2 - 22 = 0
This is a quadratic equation.
Comparing the above equation with ax2 + bx + c = 0, we get
a = 1, b = 0 and c = -22
Solution 4(i)
The given equation is x2 + 4x - 5 = 0 … (I)
Substituting x = 1 in L.H.S. of equation (I), we get
L.H.S. = (1)2 + 4(1) - 5 = 1 + 4 - 5 = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation.
Substituting x = -1 in L.H.S. of equation (I), we get
L.H.S. = (-1)2 + 4(-1) - 5 = 1 - 4 - 5 = -8
∴ LH.S. ≠ R.H.S.
∴ x = -1 is not the root of the given quadratic equation.
Solution 4(ii)
The given equation is 2m2 - 5m = 0 … (I)
Substituting m = 2 in L.H.S. of equation (I), we get
L.H.S. = 2(2)2 - 5(2) = 2(4) -10 = 8 - 10 = -2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
Putting m = ![]() in
L.H.S. of equation (I), we get
in
L.H.S. of equation (I), we get
L.H.S 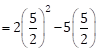

∴ L.H.S. = R.H.S.
∴ m = ![]() is the
root of the given quadratic equation.
is the
root of the given quadratic equation.
Solution 5
Given quadratic equation is kx2 - 10x + 3 = 0 … (I)
Since, x = 3 is the root of equation (I), we have
k(3)2 - 10(3) + 3 = 0
∴ 9k - 30 + 3 = 0
∴ 9k - 27 = 0
∴ 9k = 27
∴ k = 3
Solution 6
![]() is
a root of quadratic equation 5m2 + 2m + k = 0
is
a root of quadratic equation 5m2 + 2m + k = 0
∴
Put m = ![]() in the equation.
in the equation.
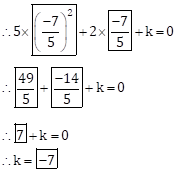
Quadratic Equations Exercise Ex. 2.2
Solution 1(i)
The given quadratic equation is x2 - 15x + 54 = 0
∴ x2 - 9x - 6x + 54 = 0
∴ x(x - 9) - 6(x - 9) = 0
∴ (x - 9)(x - 6) = 0
∴ x - 9 = 0 or x - 6 = 0
∴ x = 9 or x = 6
∴ 9 and 6 are the roots of the given quadratic equation.
Solution 1(ii)
The given quadratic equation is x2 + x - 20 = 0
∴ x2 + 5x - 4x - 20 = 0
∴ x2 + 5x - 4x - 20 = 0
∴ x(x + 5) - 4(x + 5) = 0
∴ (x + 5)(x - 4) = 0
∴ x + 5 = 0 or x - 4 = 0
∴ x = -5 or x = 4
∴ -5 and 4 are the roots of the given quadratic equation.
Solution 1(iii)
The given quadratic equation is 2y2 + 27y + 13 = 0
∴ 2y2 + 26y + y + 13 = 0
∴ 2y2 + 26y + y + 13 = 0
∴ 2y(y + 13) + 1(y + 13) = 0
∴ (y + 13)(2y + 1) = 0
∴ y + 13 = 0 or 2y + 1 = 0
∴ y = -13 or 2y = -1
∴ y = -13 or y = ![]()
∴ -13 and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(iv)
The given quadratic equation is 5m2 = 22m + 15
∴ 5m2 = 22m + 15
∴ 5m2 - 25m + 3m - 15 = 0
∴ 5m2 - 25m + 3m - 15 = 0
∴ 5m(m - 5) + 3(m - 5) = 0
∴ (m - 5)(5m + 3) = 0
∴ m - 5 = 0 or 5m + 3 = 0
∴ m = 5 or 5m = -3
∴ m = 5 or y = ![]()
∴ 5 and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(v)
The given
quadratic equation is 2x2 - 2x +![]() =
0
=
0
Multiplying both sides of the above equation by 2
∴ 4x2 - 4x + 1 = 0
∴ 4x2 - 2x - 2x + 1 = 0
∴ 4x2 - 2x - 2x + 1 = 0
∴ 2x(2x - 1) - (2x - 1) = 0
∴ (2x - 1)(2x - 1) = 0
∴ 2x - 1 = 0 or 2x - 1 = 0
∴ x = ![]() or x =
or x = ![]()
∴ ![]() and
and
![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(vi)
The given
quadratic equation is 6x - ![]() = 1
= 1
Multiplying both sides of the above equation by x
∴ 6x2 - 2 = x
∴ 6x2 - x - 2 = 0
∴ 6x2 - 4x + 3x - 2 = 0
∴ 6x2 - 4x + 3x - 2 = 0
∴ 2x(3x - 2) + 1(3x - 2) = 0
∴ (3x - 2)(2x + 1) = 0
∴ 3x - 2 = 0 or 2x + 1 = 0
∴ x = ![]() or x =
or x = ![]()
∴ ![]() and
and
![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(vii)
![]()
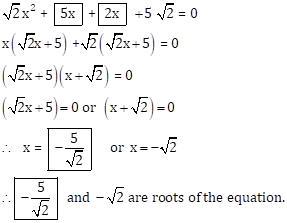
Solution 1(viii)
The given
quadratic equation is 3x2 - ![]() +
2 = 0
+
2 = 0
∴ ![]()

∴ ![]() and
and
![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(ix)
The given quadratic equation is 2m(m - 24) = 50
Dividing the above equation by 2
∴ m(m - 24) = 25
∴ m2 - 24m = 25
∴ m2 - 24m - 25 = 0
∴ m2 - 25m + m - 25 = 0
∴ m2 - 25m + m - 25 = 0
∴ m(m - 25) + 1(m - 25) = 0
∴ (m - 25)(m + 1) = 0
∴ m - 25 = 0 or m + 1 = 0
∴ m = 25 or m = -1
∴ 25 and -1 are the roots of the given quadratic equation.
Solution 1(x)
The given quadratic equation is 25m2 = 9
∴ 25m2 - 9 = 0
∴ (5m)2 - (3)2 = 0
Since, a2 - b2 = (a - b)(a + b)
∴ (5m - 3)(5m + 3) = 0
∴ 5m - 3 = 0 or 5m + 3 = 0
∴ 5m = 3 or 5m = -3
∴ ![]()
∴ ![]() and
and
![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(xi)
The given quadratic equation is 7m2 = 21m
∴ 7m2 - 21m = 0
Dividing both sides of the above equation by 7
∴ m2 - 3m = 0
∴ m(m - 3) = 0
∴ m = 0 or m - 3 = 0
∴ m = 0 or m = 3
∴ 0 and 3 are the roots of the given quadratic equation.
Solution 1(xii)
The given quadratic equation is m2 - 11 = 0
![]()
Since, a2 - b2 = (a - b)(a + b)
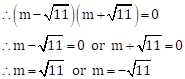
∴ ![]() and
and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Quadratic Equations Exercise Ex. 2.3
Solution 1(i)
If x2 + x - 20 = (x + a)2
∴ x2 + x + k = x2 + 2ax + a2
Comparing the terms, we get
x = 2ax and k = a2
∴ ![]() and
and 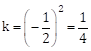
Now, x2 + x - 20 = 0

Taking square root on both the sides, we get
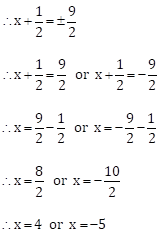
∴ 4 and -5 are the roots of the given quadratic equation.
Solution 1(ii)
If x2 + 2x - 5 = (x + a)2
∴ x2 + 2x + k = x2 + 2ax + a2
Comparing the terms, we get
2x = 2ax and k = a2
∴ a = 1 and k = 1
Now, x2 + 2x - 5 = 0
∴ x2 + 2x + 1 - 1 - 5 = 0
∴ (x + 1)2 - 6 = 0
∴ (x + 1)2 = 6
Taking square root on both the sides, we get
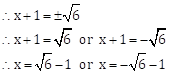
∴
![]() and
and
![]() are
the roots of the given quadratic equation.
are
the roots of the given quadratic equation.
Solution 1(iii)
The given quadratic equation is m2 - 5m = -3
∴ m2 - 5m + 3 = 0
If m2 - 5m + k = (m + a)2
∴ m2 - 5m + k = m2 + 2am + a2
Comparing the terms, we get
-5m = 2am and k = a2
![]()
Now, m2 - 5m + 3 = 0
![]()
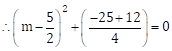

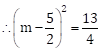
Taking square root on both the sides, we get
![]()
![]()
![]()
∴
![]() and
and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(iv)
The given quadratic equation is 9y2 - 12y + 2 = 0
Dividing both sides by 9, we get
![]()
If ![]()
![]()
Comparing the terms, we get
![]()
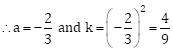
Now, ![]()
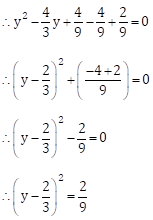
Taking square root on both the sides, we get

![]()
∴ ![]() and
and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(v)
The given quadratic equation is 2y2 + 9y + 10 = 0
Dividing both sides by 2, we get
![]()
If ![]()
![]()
Comparing the terms, we get
![]()

Now, ![]()
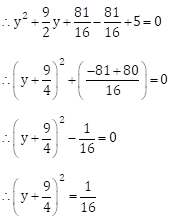
Taking square root on both the sides, we get
![]()
![]()
![]()
![]()
![]()
∴ -2 and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Solution 1(vi)
The given quadratic equation is 5x2 = 4x + 7
∴ 5x2 - 4x - 7 = 0
Dividing both sides by 5, we get
![]()
If ![]()
![]()
Comparing the terms, we get
![]()
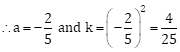
Now, ![]()
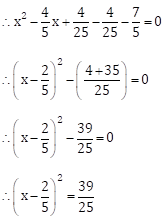
Taking square root on both the sides, we get
![]()
![]()
![]()
![]()
∴ ![]() and
and ![]() are the
roots of the given quadratic equation.
are the
roots of the given quadratic equation.
Quadratic Equations Exercise Ex. 2.4
Solution 1(i)
The above equation is x2 - 7x + 5 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = -7 and c = 5
Solution 1(ii)
The above equation is 2m2 = 5m - 5
∴ 2m2 - 5m + 5 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 2, b = -5 and c = 5
Solution 1(iii)
The above equation is y2 = 7y
∴ y2 - 7y = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = -7 and c = 0
Solution 2(i)
The above equation is x2 + 6x + 5 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = 6 and c = 5
∴ b2 - 4ac = (6)2 - (4 × 1 × 5)
= 36 - 20
= 16
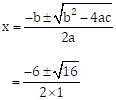
![]()
![]()
![]()
∴ x = -1 or x = -5
∴ The roots of the given quadratic equation are -1 and -5.
Solution 2(ii)
The above equation is x2 - 3x - 2 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = -3 and c = -2
∴ b2 - 4ac = (-3)2 - 4 × 1 × (-2)
= 9 + 8
= 17
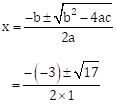
![]()
![]()
∴
The roots of the given quadratic equation are ![]() and
and ![]()
Solution 2(iii)
The above equation is 3m2 + 2m - 7 = 0 … (I)
Comparing above equation (I) with am2 + bm + c = 0, we get
a = 3, b = 2 and c = -7
∴ b2 - 4ac = (2)2 - 4 × 3 × (-7)
= 4 + 84
= 88
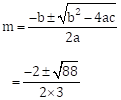
![]()
![]()
![]()
∴
The roots of the given quadratic equation are ![]() and
and ![]()
Solution 2(iv)
The above equation is 5m2 - 4m - 2 = 0 … (I)
Comparing above equation (I) with am2 + bm + c = 0, we get
a = 5, b = -4 and c = -2
∴ b2 - 4ac = (-4)2 - 4 × 5 × (-2)
= 16 + 40
= 56
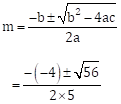
![]()
![]()
![]()
∴
The roots of the given quadratic equation are ![]() and
and ![]()
Solution 2(v)
The
above equation is y2 + ![]() = 2
= 2
∴ 3y2 + y = 6
∴ 3y2 + y - 6 = 0 … (I)
Comparing above equation (I) with ay2 + by + c = 0, we get
a = 3, b = 1 and c = -6
∴ b2 - 4ac = (1)2 - 4 × 3 × (-6)
= 1 + 72
= 73
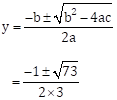
![]()
![]()
∴
The roots of the given quadratic equation are ![]() and
and ![]()
Solution 2(vi)
The above equation is 5x2 + 13x + 8 = 0 … (I)
Comparing above equation (I) with ay2 + by + c = 0, we get
a = 5, b = 13 and c = 8
∴ b2 - 4ac = (13)2 - 4 × 5 × (8)
= 169 - 160
= 9
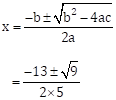
![]()
![]()
![]()
![]()
∴
The roots of the given quadratic equation are -1 and ![]()
Solution 3
Given equation is
![]()
Comparing the above equation with ax2 + bx + cx = 0, we get
![]()
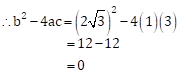

![]()
![]()
∴ The
roots of the given quadratic equation are ![]()
Quadratic Equations Exercise Ex. 2.5
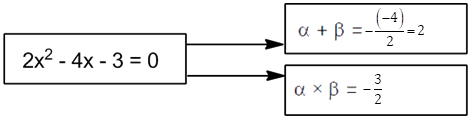
Solution 1
(1)

(2)

(3)
Solution 2
(1)
The above equation is x2 + 7x - 1 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = 7 and c = -1
∴ b2 - 4ac = (7)2 - 4 × 1 × (-1)
= 49 + 4
= 53
∴ Discriminant = 53
(2)
The above equation is 2y2 - 5y + 10 = 0 … (I)
Comparing above equation (I) with ay2 + by + c = 0, we get
a = 2, b = -5 and c = 10
∴ b2 - 4ac = (-5)2 - 4 × 2 × 10
= 25 - 80
= -55
∴ Discriminant = -55
(3)
The above
equation is ![]() x2
+ 4x +
x2
+ 4x +![]() = 0 … (I)
= 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a =![]() , b = 4
and c =
, b = 4
and c = ![]()
∴ b2 -
4ac = (4)2 - 4 × ![]() ×
× ![]()
= 16 - 16
= 0
∴ Discriminant = 0
Solution 3
(1)
The above equation is x2 - 4x + 4 = 0 … (I)
Comparing above equation (I) with ax2 + bx + c = 0, we get
a = 1, b = -4 and c = 4
∴ b2 - 4ac = (-4)2 - 4 × 1 × 4
= 16 - 16
= 0
Since, ∆ = 0
∴ Roots of the given quadratic equation are real and equal.
(2)
The above equation is 2y2 - 7y + 2 = 0 … (I)
Comparing above equation (I) with ay2 + by + c = 0, we get
a = 2, b = -7 and c = 2
∴ b2 - 4ac = (-7)2 - 4 × 2 × 2
= 49 - 16
= 33
Since, ∆ > 0
∴ Roots of the given quadratic equation are real and distinct.
(3)
The above equation is m2 + 2m + 9 = 0 … (I)
Comparing above equation (I) with am2 + bm + c = 0, we get
a = 1, b = 2 and c = 9
∴ b2 - 4ac = 22 - 4 × 1 × 9
= 4 - 36
= -32
Since, ∆ < 0
∴ Roots of the given quadratic equation are not real.
Solution 4
(1)
Let α = 0 and β = 4
∴ α + β = 0 + 4 = 4 and α×β = 0 × 4 = 0
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - 4x + 0 = 0
∴ x2 - 4x = 0
(2)
Let α = 3 and β = -10
∴ α + β = 3 + (-10) = -7 and α×β = 3 × (-10) = -30
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - (-7) x + (-30) = 0
∴ x2 +7x - 30 = 0
(3)
Let ![]()
∴ ![]()
The quadratic equation is
x2 - (α + β) x + α×β = 0
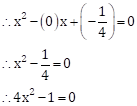
(4)
Let ![]()
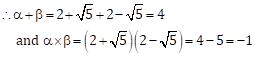
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - 4x + (-1) = 0
∴ x2 - 4x - 1 = 0
Solution 5
The equation is
x2 - 4kx + k + 3 = 0 … (I)
Comparing equation (I) with the equation ax2 + bx + c = 0, we get
a = 1, b = -4k and c = k + 3 … (II)
Let α and β be the roots of the quadratic equation.
![]()
As per the condition given in the question, we have
α+β = 2 αβ
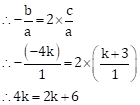 …
From equation (II)
…
From equation (II)
∴ 4k - 2k = 6
∴ 2k = 6
∴ k = 3
Solution 6
Given quadratic equation is y2 - 2y - 7 = 0 … (I)
Comparing equation (I) with the equation ay2 + by + c = 0, we get
a = 1, b = -2 and c = -7
Since, α and β be the roots of equation (I)
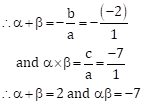
(1)
Now, ![]()

(2)
Also, ![]()

Solution 7
(1)
The quadratic equation is 3y2 + ky + 12 = 0
Comparing the above equation with the equation ay2 + by + c = 0, we get
a = 3, b = k and c = 12
Since, the roots are real and equal.
∴ Discriminant (∆) = 0
∴ b2 - 4ac = 0
∴ k2 - 4(3)(12) = 0
∴ k2 - 122 = 0
Since, a2 - b2 = (a - b)(a + b)
∴ (k - 12)(k + 12) = 0
∴ k - 12 = 0 or k + 12 = 0
∴ k = 12 or k = -12
(2)
The quadratic equation is kx (x - 2) + 6 = 0
∴ kx2 - 2kx + 6 = 0
Comparing the above equation with the equation ax2 + bx + c = 0, we get
a = k, b = -2k and c = 6
Since, the roots are real and equal.
∴ Discriminant (∆) = 0
∴ b2 - 4ac = 0
∴ (-2k)2 - 4(k)(6) = 0
∴ 4k2 - 24k = 0
∴ 4k(k - 6) = 0
∴ 4k = 0 or k - 6 = 0
∴ k = 0 or k = 6
But k = 0 is not possible as the quadratic coefficient becomes zero.
∴ k = 6
Quadratic Equations Exercise Ex. 2.6
Solution 1
Let the present age of Pragati be x years.
2 years ago, age of Pragati = (x - 2) years
After 3 years, age of Pragati = (x + 3) years
As per the condition given in the question,
(x - 2)(x + 3) = 84
∴ x(x + 3) - 2(x + 3) = 84
∴ x2 + 3x - 2x - 6 = 84
∴ x2 + x - 6 - 84 = 0
∴ x2 + x - 90 = 0
∴ x2 + 10x - 9x - 90 = 0
∴ x(x + 10) - 9(x + 10) = 0
∴ (x + 10)(x - 9) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x - 9 = 0
∴ x = -10 or x = 9
Since the age can't be negative, we get
x = 9
Hence, Pragati's present age is 9 years.
Solution 2
Let the first even natural number be x.
∴ The next consecutive even natural number will be (x + 2).
From the given condition, we have
x2 + (x + 2)2 = 244
∴ x2 + x2 + 4x + 4 = 244
∴ 2x2 + 4x + 4 - 244 = 0
∴ 2x2 + 4x - 240 = 0
Dividing both sides of above equation by 2
∴ x2 + 2x - 120 = 0
∴ x2 + 12x - 10x - 120 = 0
∴ x(x + 12) - 10(x + 12) = 0
∴ (x + 12)(x - 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 12 = 0 or x - 10 = 0
∴ x = -12 or x = 10
But, natural number cannot be negative.
∴ x = 10
And, x + 2 = 10 + 2 = 12
∴ The two consecutive even natural numbers are 10 and 12.
Solution 3
Number of trees in a column is x.
∴ Number of trees in a row = x + 5
∴ Total number of trees = x × (x + 5)
From the given condition, we have
x(x + 5) = 150
∴ x2 + 5x = 150
∴ x2 + 5x - 150 = 0
∴ x2 + 15x - 10x - 150 = 0
∴ x(x+ 15) - 10(x + 15) = 0
∴ (x + 15)(x - 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 15 = 0 or x - 10 = 0
∴ x = -15 or x = 10
Since, the number of trees cannot be negative.
∴ x = 10
∴ Number of trees in a column is 10.
∴ Number of trees in a row = x + 5 = 10 + 5 = 15
∴ Number of trees in a row is 15.
Solution 4
Let the present age of Kishor be x years.
∴ Present age of Vivek = (x + 5) years
From the given condition, we have
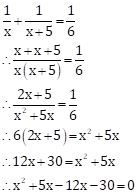
∴ x2- 7x - 30 = 0
∴ x2- 10x + 3x - 30 = 0
∴ x(x - 10) + 3(x - 10) = 0
∴ (x - 10)(x + 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x - 10 = 0 or x + 3 = 0
∴ x = 10 or x = -3
Since, the age cannot be negative.
∴ x = 10
And, x + 5 = 10 + 5 = 15
∴ Present ages of Kishor and Vivek are 10 years and 15 years respectively.
Solution 5
Let Suyash score x marks in the first test.
∴ Score in the second test = x + 10
From the given condition, we have
5(x + 10) = x2
∴ 5x + 50 = x2
∴ x2- 5x - 50 = 0
∴ x2- 10x + 5x - 50 = 0
∴ x(x - 10) + 5(x - 10) = 0
∴ (x - 10)(x + 5) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x - 10 = 0 or x + 5 = 0
∴ x = 10 or x = - 5
Since, the score cannot be negative.
∴ x = 10
∴ The score of Suyash in the first test is 10 marks.
Solution 6
Let Mr. Kasam make x number of pots on daily basis.
Production cost of each pot = Rs. (10x + 40)
From the given condition, we have
x(10x + 40) = 600
∴ 10x2 + 40x = 600
∴ 10x2 + 40x - 600 = 0
Dividing both sides of above equation by 10, we get
x2 + 4x - 60 = 0
∴ x2 + 10x - 6x - 60 = 0
∴ x(x + 10) - 6(x + 10) = 0
∴ (x + 10)(x - 6) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x - 6 = 0
∴ x = -10 or x = 6
Since, the number of pots cannot be negative.
∴ x = 6
∴ Production cost of each pot = (10x + 40)
= Rs [(10×6)+ 40]
= Rs (60 + 40)
= Rs 100
Production cost of one pot is Rs 100 and the number of pots Mr. Kasam makes per day is 6.
Solution 7
Let the speed of water current be x km/hr.
Speed of boat in still water is given as 12 km/hr. (x < 12)
In upstream, speed of the water current decreases the speed of the boat.
Whereas, in downstream, speed of the water current increases the speed of the boat.
∴ speed of the boat in upstream = (12 - x) km/hr
and speed of the boat in downstream = (12 + x) km/hr
As,
![]()
∴
Time required to cover 36 km upstream ![]() hrs
hrs
Time
required to cover 36 km downstream ![]() hrs
hrs
From the given condition, we have
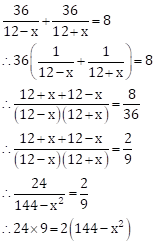
∴ 216 = 288 - 2x2
∴ 2x2 + 216 - 288 = 0
∴ 2x2 - 72 = 0
Dividing both sides of above equation by 2, we get
x2 - 36 = 0
∴ x2 = 36
Taking square root on both the sides
∴ x = ±6
Since, the speed can't be negative.
∴ x = 6
∴ The speed of water current is 6 km/hr.
Solution 8
Let Nishu take x days to complete the work alone.
∴ Total
work done by Nishu in 1 day ![]()
Also, Pintu takes (x + 6) days to complete the work alone.
∴ Total
work done by Pintu in 1 day ![]()
∴ Total
work done by both in 1 day ![]()
It is given that both take 4 days to complete the work together.
∴ Total
work done by both in 1 day ![]()
From the given condition, we have
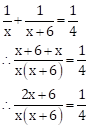
∴ 4(2x + 6) = x(x + 6)
∴ 8x + 24 = x2 + 6x
∴ x2 + 6x - 8x - 24 = 0
∴ x2- 2x - 24 = 0
∴ x2- 6x + 4x - 24 = 0
∴ x(x - 6)+ 4(x - 6) = 0
∴ (x - 6) (x + 4) = 0
∴ x - 6 = 0 or x + 4 = 0
∴ x = 6 or x = -4
But, number of days cannot be negative,
∴ x = 6 and x + 6 = 6 + 6 = 12
∴ Number of days taken by Nishu and Pintu to complete the work alone is 6 days and 12 days respectively.
Solution 9
Let the natural number be x.
∴ Divisor = x, Quotient = 5x + 6
Also, Dividend = 460 and Remainder = 1
Since, Dividend = Divisor × Quotient + Remainder
∴ 460 = x × (5x + 6) + 1
∴ 460 = 5x2 + 6x + 1
∴ 5x2 + 6x + 1 - 460 = 0
∴ 5x2 + 6x - 459 = 0
∴ 5x2 - 45x + 51x - 459 = 0
∴ 5x(x - 9) + 51(x - 9) = 0
∴ (x - 9)(5x + 51) = 0
∴ x - 9 = 0 or 5x + 51 = 0
∴ x = 9
or ![]()
Since, the natural number cannot be negative,
∴ x = 9
∴ Quotient = 5x + 6 = 5(9) + 6 = 45 + 6 = 51
∴ Quotient is 51 and divisor is 9.
Solution 10
Given: ⎕ABCD is a trapezium and AB || CD
Now, Area of trapezium
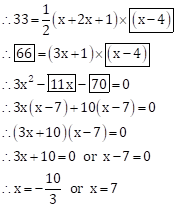
But length is never negative.
![]()
AB = 7 cm, CD = 15 cm, AD = BC = 5 cm
Quadratic Equations Exercise Problem Set 2
Solution 1(i)
The equation x(x + 5) = 2
i.e. x2 + 5x = 2
It is a quadratic equation as the degree is 2.
Solution 1(ii)
The equation x2 + 4x = 11 + x2
i.e. 4x - 11 = 0
This is not quadratic as the degree of this equation is 1.
Solution 1(iii)
The given equation is x2 + kx + k = 0
Comparing above equation with ax2 + bx + c = 0, we get
a = 1, b = k, c = k
Since, the roots are real and equal.
∴ ∆ = 0
∴ b2 - 4ac = 0
∴ k2 - 4×1×k = 0
∴ k2 - 4k = 0
∴ k(k - 4) = 0
∴ k = 0 or k - 4 = 0
∴ k = 0 or k = 4
Solution 1(iv)
Given quadratic equation is √2x2 - 5x + √2 = 0
Comparing above equation with ax2 + bx + c = 0, we get
![]()
Discriminant (∆) = b2 - 4ac
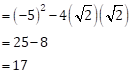
∴ Discriminant = 17
Solution 1(v)
Let α = 3 and β = 5
The quadratic equation with the roots α and β is given by
x2 - (α + β)x + α×β = 0
∴ x2 - (3+5)x + 3×5 = 0
∴ x2 - 8x + 15 = 0
∴ The required quadratic equation is x2 - 8x + 15 = 0.
Solution 1(vi)
For a quadratic equation ax2 + bx + c = 0
Sum
of the roots ![]()
In quadratic equation, 3x2 + 15x +3 = 0
![]()
∴ Sum of roots = -5
∴ The quadratic equation whose sum of roots is -5 is 3x2 + 15x +3 = 0.
Solution 1(vii)
The
given quadratic equation is ![]()
Dividing
the above equation by ![]() we get
we get
m2 - m + 1 = 0
Comparing above equation with am2 + bm + c = 0, we get
a = 1, b = -1, c = 1
Now, discriminant (∆) = b2 - 4ac
∴ ∆ = (-1)2 - 4(1)(1) = 1 - 4 = -3
Since ∆ < 0
So, the roots are not real.
Solution 1(viii)
Given equation is x2 + mx - 5 = 0 … (I)
As 2 is one of the roots of equation (I)
∴ 22 + m × 2 - 5 = 0
∴ 4 + 2m - 5 = 0
∴ 2m - 1 = 0
![]()
Solution 2
(1)
The equation is x2 + 2x + 11 = 0
Here, x is the only variable and maximum index of the variable is 2.
Also, a = 1, b = 2, c = 11 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
(2)
The equation is x2 - 2x + 5 = x2
i.e. -2x + 5 = 0
Here, x is the only variable and maximum index of the variable is 1.
∴ The given equation is not a quadratic equation.
(3)
The equation is (x + 2)2 = 2x2
i.e. x2 + 4x + 4 = 2x2
i.e. x2 - 4x - 4 = 0
Here, x is the only variable and maximum index of the variable is 2.
Also, a = 1, b = -4, c = -4 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.
Solution 3
(1)
The equation is 2y2 - y + 2 = 0
Comparing above equation with ay2 + by +c = 0, we get
a = 2, b = -1, c = 2
Discriminant (∆) = b2 - 4ac
∴ ∆ = (-1)2 - 4(2)(2)
= 1 - 16
= -15
(2)
The equation is 5m2 - m = 0
Comparing above equation with am2 + bm +c = 0, we get
a = 5, b = -1, c = 0
Discriminant (∆) = b2 - 4ac
∴ ∆ = (-1)2 - 4(5)(0)
= 1 - 0
= 1
(3)
The
equation is ![]()
Comparing above equation with ax2 + bx +c = 0, we get
![]()
Discriminant (∆) = b2 - 4ac
![]()
= 1 + 20
= 21
Solution 4
As -2 is one of the roots of the equation 2x2 + kx - 2 = 0.
∴ Putting x = -2 in the given equation, we get
2(-2)2 + k(-2) - 2 = 0
∴ 8 - 2k - 2 = 0
∴ 6 - 2k = 0
∴ 2k = 6
∴ k = ![]()
∴ k = 3
Solution 5
(1)
Let α = 10 and β = -10
∴ α + β = 10 - 10 = 0 and α×β = 10 × (-10) = -100
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - 0×x + (-100) = 0
∴ x2 - 100 = 0
(2)
Let
![]()
∴ ![]()
![]()
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - 2x + (-44) = 0
∴ x2 - 2x - 44 = 0
(3)
Let α = 0 and β = 7
∴ α + β = 0 + 7 = 7 and αβ = 0×7 = 0
The quadratic equation is
x2 - (α + β) x + α×β = 0
∴ x2 - 7x + 0 = 0
∴ x2 - 7x = 0
Solution 6
(1)
The equation is 3x2 - 5x + 7 = 0
Comparing above equation with ax2 + bx + c = 0, we get
a = 3, b = -5, c = 7
Discriminant (∆) = b2 - 4ac
∴ ∆ = (-5)2 - 4(3)(7)
= 25 - 84
= -59
Since, ∆ < 0
∴ The roots are not real.
(2)
The equation is √3x2 + √2x - 2√3 = 0
Comparing above equation with ax2 + bx + c = 0, we get
![]()
Discriminant (∆) = b2 - 4ac
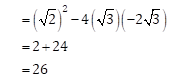
Since, ∆ > 0
∴ The roots are real and unequal.
(3)
The equation is m2 - 2m + 1 = 0
Comparing above equation with am2 + bm + c = 0, we get
a = 1, b = -2, c = 1
Discriminant (∆) = b2 - 4ac
∴ ∆ = (-2)2 - 4(1)(1)
= 4 - 4
= 0
Since, ∆ = 0
∴ The roots are real and equal.
Solution 7(i)
Given
equation is ![]()
Cross multiplying both the sides, we get
x2 = x + 5
∴ x2 - x - 5 = 0 … (I)
Comparing equation (I) with ax2 + bx + c = 0, we get
a = 1, b = -1, c = -5
∴ b2 - 4ac = (-1)2 - 4(1)(-5)
= 1 + 20
= 21
Now,
![]()
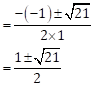
![]()
∴ The
roots of the given quadratic equation are ![]()
Solution 7(ii)
Given
equation is ![]()
Multiplying both sides by 10, we get
10x2 - 3x - 1 = 0
∴ 10x2 - 5x + 2x - 1 = 0
∴ 5x(2x - 1) + 1(2x - 1) = 0
∴ (2x - 1)(5x + 1) = 0
∴ 2x - 1 = 0 or 5x + 1 = 0
![]()
∴ The
roots of the given quadratic equation are ![]()
Solution 7(iii)
Given equation is (2x + 3)2 = 25
∴ 4x2 + 12x + 9 = 25
∴ 4x2 + 12x + 9 - 25 = 0
∴ 4x2 + 12x - 16 = 0
Dividing the above equation by 4, we get
∴ x2 + 3x - 4 = 0
∴ x2 + 4x - x - 4 = 0
∴ x(x + 4) - 1(x + 4) = 0
∴ (x + 4)(x - 1) = 0
∴ x + 4 = 0 or x - 1 = 0
∴ x = -4 or x = 1
∴ The roots of the given quadratic equation are -4 and 1.
Solution 7(iv)
Given equation is m2 + 5m + 5 = 0 … (I)
Comparing equation (I) with am2 + bm + c = 0, we get
a = 1, b = 5, c = 5
∴ b2 - 4ac = (5)2 - 4(1)(5)
= 25 - 20
= 5
Now,
![]()
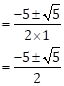
![]()
∴ The
roots of the given quadratic equation are ![]()
Solution 7(v)
Given equation is 5m2 + 2m + 1 = 0
Comparing above equation with am2 + bm + c = 0, we get
a = 5, b = 2, c = 1
∴ b2 - 4ac = (2)2 - 4(5)(1)
= 4 - 20
= -16
Since, b2 - 4ac < 0
∴ The roots of the given equation are not real.
Solution 7(vi)
Given equation is x2 - 4x - 3 = 0
Comparing above equation with ax2 + bx + c = 0, we get
a = 1, b = -4, c = -3
∴ b2 - 4ac = (-4)2 - 4(1)(-3)
= 16 + 12
= 28
Now,
![]()
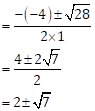
![]()
∴ The
roots of the given quadratic equation are ![]()
Solution 8
Given quadratic equation is (m - 12)x2 + 2(m - 12)x + 2 = 0
Comparing the above equation with ax2 + bx + c = 0, we get
a = m - 12, b = 2(m - 12), c = 2
Now,
∆ = b2- 4ac
= [2(m - 12)]2 - 4 × (m - 12) × 2
= 4(m - 12)2 - 8(m - 12)
= 4(m - 12) (m - 12 - 2)
∴ ∆ = 4(m - 12) (m - 14)
Since, the roots are real and equal.
∴ ∆ = 0
∴ 4(m - 12) (m - 14) = 0
∴ (m - 12) (m - 14) = 0
∴ m - 12 = 0 or m - 14 = 0
∴ m = 12 or m = 14
If m = 12, then quadratic coefficient becomes zero.
∴ m ≠ 12
∴ m = 14
Solution 9
Let α and β be the roots of the quadratic equation.
From the first condition, we have
α + β = 5 … (I)
From the second condition, we have
α3 + β3 = 35 … (II)
Now, (α + β)3 = α3 + 3α2β + 3αβ2 + β3
∴ (α + β)3 = α3 + β3 + 3αβ(α + β)
Using equations (I) and (II)
∴ (5)3 = 35 + 3αβ(5)
∴ 125 = 35 + 15αβ
∴ 125 - 35 = 15αβ
∴ 15αβ = 90
![]()
∴ αβ = 6
∴ The required quadratic equation is
x2 - (α + β)x + αβ = 0
i.e. x2- 5x + 6 = 0
Solution 10
Given quadratic equation is
2x2 + 2(p + q)x + p2 + q2 = 0 … (I)
Comparing the above equation with ax2 + bx + c = 0, we get
a = 2, b = 2(p + q), c = p2 + q2
Let α and β be the roots of equation (I)
![]() … (II)
… (II)
And,
![]()
Now,
![]()
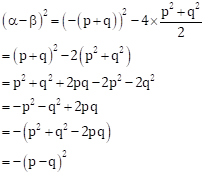
As per the given condition, roots of the required quadratic equation are
(α + β)2 and (α - β)2
Now,
sum of the roots = (α + β)2 + (α - β)2
= [-(p + q)]2 + (-(p - q)2)
= (p + q)2 - (p - q)2
= p2 + q2 + 2pq - (p2 + q2 - 2pq)
= p2 + q2 + 2pq - p2 - q2 + 2pq
= 4pq
Product of roots = (α + β)2 × (α - β)2
= [-(p + q)]2 [-(p - q)2]
= -(p + q)2 (p - q)2
= -[(p + q)(p - q)]2
= -(p2 - q2)2
∴ The required quadratic equation is
x2 - [(α + β)2 + (α - β)2]x + [(α + β)2 × (α - β)2] = 0
i.e. x2 - (4pq)x - (p2 - q2)2 = 0
Solution 11
Let the amount Sagar possesses be Rs x.
∴ The amount Mukund possesses = Rs (x + 50)
As per the condition, we have
x(x + 50)= 15000
∴ x2 + 50x - 15000 = 0
∴ x2 + 150x - 100x - 15000 = 0
∴ x(x + 150) - 100(x + 150) = 0
∴ (x + 150)(x - 100) = 0
∴ x + 150 = 0 or x - 100 = 0
∴ x = -150 or x = 100
Since, amount cannot be negative.
∴ x = 100 and x + 50 = 100 + 50 = 150
∴ The amount possessed by Sagar and Mukund are Rs. 100 and Rs. 150 respectively.
Solution 12
Let the two numbers be x and y (x > y).
As per the given condition, we have
x2 - y2 = 120 … (I)
y2 = 2x … (II)
Substituting y2 = 2x in equation (i), we get
x2 - 2x = 120
∴ x2- 2x - 120 = 0
∴ x2- 12x + 10x - 120 = 0
∴ x(x - 12) + 10(x - 12) = 0
∴ (x - 12)(x + 10) = 0
∴ x - 12 = 0 or x + 10 = 0
∴ x = 12 or x = -10
When x ≠ -10,
y2 = 2x = 2(-10) = -20 … [Since, the square of number cannot be negative]
∴ x = 12
Smaller number = y2 =2x
∴ y2 = 2 × 12
∴ y2 = 24
∴ y = ± √24 …[Taking square root of both sides]
∴ The smaller number is √24 and greater number is 12 or the smaller number is -√24 and greater number is 12.
Solution 13
Let the number of students be x.
Total number of oranges = 540 … (Given)
∴ The
number of oranges each student gets ![]()
When there are 30 more students, we have
Total number of students = (x + 30)
and
total number of oranges each student gets ![]()
As per the given condition, we have
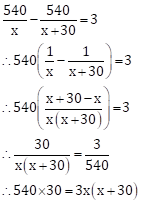
∴ 540×30 = 3x2 + 90x
∴ 3x2 + 90x - 540×30 = 0
Dividing both sides by 3, we get
x2 + 30x - 540×10 = 0
∴ x2 + 30x - 5400 = 0
∴ x2 + 90x - 60x - 5400 = 0
∴ x(x + 90) - 60(x + 90) = 0
∴ (x + 90)(x - 60) = 0
∴ x + 90 = 0 or x - 60 = 0
∴ x = -90 or x = 60
Since the number of students can't be negative.
∴ x = 60
∴ The total number of students is 60.
Solution 14
Let the breadth of the rectangular farm be x m.
∴ Length of rectangular farm = (2x + 10) m
Now, Area of rectangular farm = Length × Breadth
= (2x + 10) × x
= (2x2 + 10x) sq. m
Now,
side of square shaped pond ![]() m
m
∴ Area of square shaped pond = (side)2
![]()
According to the given condition, we have
Area of rectangular farm = 20 × Area of pond
![]()
Dividing both sides of the above equation by 2, we get
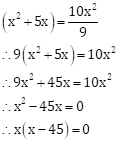
∴ x = 0 or x - 45 = 0
∴ x = 0 or x = 45
Since the breadth of the farm can't be zero.
∴ x = 45
Length of the rectangular farm = 2x + 10
= 2×45 + 10
= 90 + 10
= 100 m
Side
of the pond ![]() m
m
∴ Length and breadth of the farm and the side of pond are 100 m, 45 m and 15 m respectively.
Solution 15
Let the larger tap take x hours to fill the tank completely.
∴ Part of
tank filled by the larger tap in 1 hour ![]()
Also, the smaller tap takes (x + 3) hours to fill the tank completely.
∴ Part of
tank filled by the smaller tap in 1 hour ![]()
∴
Part
of tank filled by both the taps in 1 hour ![]()
But, the tank gets filled in 2 hours by both the taps.
∴ Part of tank filled by both the taps in 1 hour = ½
As per the given condition, we have
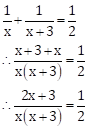
∴ 2(2x + 3) = x(x + 3)
∴ 4x + 6 = x2 + 3x
∴ x2 + 3x - 4x - 6 = 0
∴ x2- x - 6 = 0
∴ x2- 3x + 2x - 6 = 0
∴ x(x - 3) + 2(x - 3) = 0
∴ (x - 3)(x + 2) = 0
∴ x - 3 = 0 or x + 2 = 0
∴ x = 3 or x = -2
But as we know that time cannot be negative.
∴ x = 3 and x + 3 = 3 + 3 = 6
∴ The larger tap takes 3 hours and the smaller tap takes 6 hours to fill the tank completely.

