Question Paper (Section wise)
-
1) A gas can be taken from A to B via two different processes ACB and ADB. When path ACB is used 60 J of heat flows into the system. If path ADB is used work down by the system is 10 J. the heat flow into the system in path ADB is

-
40 J
-
80 J
-
100 J
-
20 J
-
-
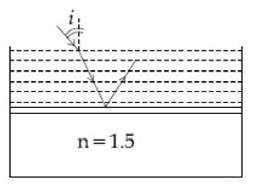
2) Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index µ. A student finds that, irrespective of what the incident angle I (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of µ is
-
-
3) A heavy ball of mass M is suspended from the ceiling car by a light string of mass m (m<<M). When the car is at rest, the speed of transverse waves in the string is 60 ms-1. When the car has acceleration a, the wave-speed increase to 60.5 ms-1. The value of a, in terms of gravitational acceleration g is closed to:
-
-
4) A hoop and a solid cylinder of same mass and radius are made of a permanent magnetic material with their magnetic moment parallel to their respective axes. But the magnetic moment of hoop is twice of solid cylinder. They are placed in a uniform magnetic field in such a manner that their magnetic moments make a small angle with the field. If the oscillation periods of hoop and cylinder are Th and Tc respectively, then:
-
Th = Tc
-
Th = 2Tc
-
Th = 1.5Tc
-
Th = 0.5c
-
-
5) The actual value of resistance R, shown in the figure is 30 ?. This is measured in an experiment as shown using the standard Formula
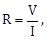 where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5 % less, then the internal resistance of the voltmeter is:
where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5 % less, then the internal resistance of the voltmeter is: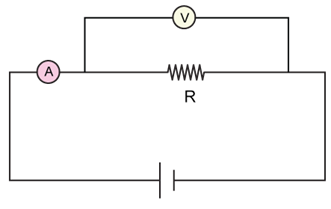
-
600 ?
-
570 ?
-
35 ?
-
350 ?
-
-
6) A cylindrical plastic bottle of negligible mass of field with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic still motion at angular frequency ?. If the radius of the bottle is 2.5 cm then ? is closed to: (density of water = 103 kg/m3)
-
7.95 rads-1
-
1.25 rads-1
-
2.50 rads-1
-
5.00 rads-1
-
-
7) In the given circuit the current through Zener Diode is close to:

-
0.0 mA
-
6.7 mA
-
4.0 mA
-
6.0 mA
-
-
8) An amplitude modulated signal is given by
V (t) = 10 [1 + 0.6cos (2.2 × 104t) sin (5.5 × 105) t]. Here t is in seconds. The seconds. The sideband frequencies (in kHz) are. [Given π = 22/7]
-
1785 and 1715
-
1785 and 1715
-
89.25 and 85.75
-
892.5 and 857.5
-
-
9) A liquid of density ρ is coming out of a hose pipe of radius a with horizontal speed ν and hits a mesh. 50% of the liquid passes through the mesh unaffected. 25% losses all of its momentum and 25% comes back with the same speed. The resultant pressure on the mesh will be:
-
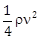
-
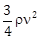
-
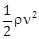
-
pv2
-
-
10) In the circuit shown, find C if the effective capacitance of the whole circuit is to be 0.5 µF. All values in the circuit are in µF.
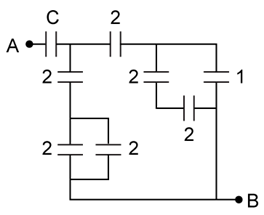
-
-
11) A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7 × 103 kg/m3 and its Young’s modulus is 9.27 × 1010 Pa. What will be the fundamental frequency of the longitudinal vibrations?
-
7.5 kHz
-
5 kHz
-
2.5 kHz
-
10 kHz
-
-
12) A resonance tube is old and has jagged end. It is still used in the laboratory to determine velocity of sound in air. A tuning fork of frequency 512 Hz produces first resonance when the tube is filled with water to a mark 11 cm below a reference mark, near the open end of the tube. The experiment is repeated with another fork of frequency 256 Hz which produces first resonance when water reaches a mark 27 cm below the reference mark.
The velocity of sound in air, obtained in the experiment is close to:
-
322 ms-1
-
341 ms-1
-
335 ms-1
-
328 ms-1
-
-
13) In the circuit shown, a four wire potentiometer is made of a 400 cm long wire, which extends between A and B. The resistance per unit length of the potentiometer wire is r = 0.01?/cm, If an ideal voltmeter is connected as shown with jockey J at 50 cm from end A, the expected reading of the voltmeter will be.
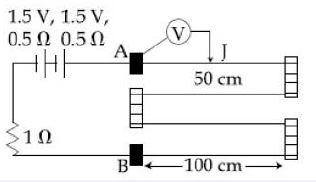
-
0.75V
-
0.20V
-
0.25V
-
0.50V
-
-
14) A common emitter amplifier circuit, built using an npn transistor, is shown in the figure. Its dc current gain is 250, Rc = 1k? and Vcc = 10V. What is the minimum base current for VCE to reach saturation?
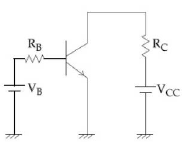
-
7 µA
-
40 µA
-
10 µA
-
100 µA
-
-
15) 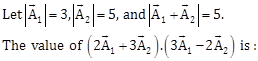
-
-106.5
-
-112.5
-
-118.5
-
-99.5
-
-
16) A system of three charges are placed as shown in the figure:
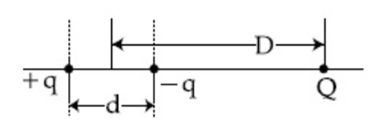
If D >> d, the potential energy of the system is best given by:
-
-
17) An HCl molecule has rotational, translational and vibrational motions. If the rms velocity of HCl molecules in its gaseous phase is ?, m is its mass and kB is Boltzmann constant, then its temperature will be:
-
-
18) Taking the wavelength of first Balmer line in hydrogen spectrum (n = 3 to n = 2) as 660 nm, the wavelength of the 2nd Balmer line (n =4 to n = 2) will be
-
889.2 nm
-
642.7 nm
-
488.9 nm
-
388.9 nm
-
-
19) In an experiment, brass and steel wires of length 1 m each with areas of cross section 1 mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress requires to produce a new elongation of 0.2 mm is [Given, the Young’s Modulus for steel and brass are respectively 120 × 109 N/m2 and 60 × 109 N/m2]
-
8 × 106 N/m2
-
0.2 × 106 N/m2
-
1.2 × 106 N/m2
-
4.0 × 106 N/m2
-
-
20) In Li++, electron in first Bohr orbit is excited to a level by a radiation of wavelength ?. When the ion gets deexcited to the ground state in all possible ways (including intermediate emission) a total of six spectral lines are observed. What is the value of ??
(Given: h = 6.63 × 1034 js; e = 3 × 108 ms–1)
-
10.8 nm
-
11.4 nm
-
9.4 nm
-
12.3 nm
-
-
21) A spaceship orbits around a planet at a height of 20 km from surface. Assuming that only gravitational field of the plant acts on the spaceship. What will be the number of complete revolutions made by the spaceship in 24 hours around the plane?
[Given: Mass of plane = 8 × 1022 kg, Radius of planet = 2 × 106 m, Gravitational constant G = 6.67 × 10-11 Nm2/kg2]
-
22) The value of numerical aperture of the objective lens of a microscope is 1.25. If light of wavelength 5000 A is used, the minimum separation between two points, to be seen as distinct, will be _____× 10-7 m.
-
23) A thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of 40 ? rad s-1 about its axis, perpendicular to its plane. If the magnetic field at its centre is 3.8 × 10-9 T, then the charge carried by the ring is close to ________ ?C.
(µ0 = 4? × 10-7N/A2)
-
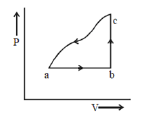
24) A sample of an ideal gas is taken through the cyclic process abca as shown in the figure. The change in the internal energy of the gas along the path ca is – 180 J. The gas absorbs 250 J of heat along the path ab and 60 J along the path bc. The work done by the gas along the path abc is ______ J.
-
25) In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of 5?, a balance is found when the cell is connected across 40 cm of the wire. The internal resistance of the cell is ______ ?.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) Correct statements among i to iv regarding silicones are
- they are polymers with hydrophobic character
- they are biocompatible
- in general, they have high thermal stability and low dielectric strength
- usually they are resistant to oxidation and used as grease.
-
(i), (ii), (iii) and (iv)
-
(i), (ii) and (iii)
-
(i) and (ii) only
-
(i), (ii) and (iv)
-
2) The following result were obtained during kinetic studies of the reaction
2A + B ? products
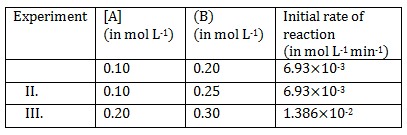
The time (in minutes) required to consume half of A is
-
5
-
10
-
1
-
100
-
-
3) The isotopes of hydrogen are
-
tritium and protium only
-
protium and deuterium only
-
protium, deuterium and tritium
-
deuterium and tritium only
-
-
4) The increasing order of nucleophilicity of the following nucleophiles is:
a. CH3CO2-
b. H2O
c. CH3SO3
d.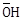
-
(b) < (c) < (a) < (d)
-
(a) < (d) < (c) < (b)
-
(d) < (a) < (c) < (b)
-
(b) < (c) < (d) < (a)
-
-
5) A reaction of cobalt (III) chloride and ethylenediamine in a 1:2 mole ratio generates two isomeric products A (violet coloured) and B (green coloured). A can show optical activity, but, B is optically inactive. What type of isomers does A and B represent?
-
Geometrical isomers
-
Coordination isomers
-
Linkage isomers
-
lonisation isomers
-
-
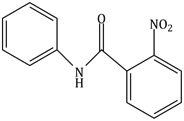
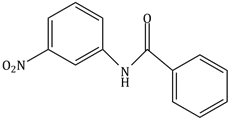
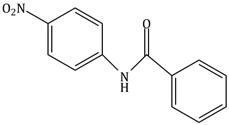
6) What will be the major product the following mono nitration reaction?
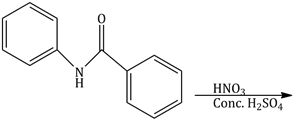
-
-
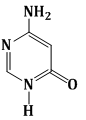
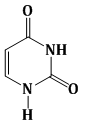
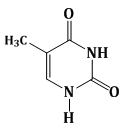
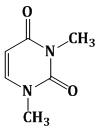
7) Among the following compounds, Which one is found in RNA?
-
-
8) The correct statement among the following is
-
(siH3)3 N is planer and less basic than (CH3)3 N.
-
(siH3)3 N is planer and more basic than (CH3)3 N.
-
(siH3)3 N is pyramidal and less basic than (CH3)3 N.
-
(siH3)3 N is pyramidal and more basic than (CH3)3 N.
-
-
9) Enthalpy of sublimation of iodine is 24 Cal g-1 at 200°C. If specific heat of l2 (s) and l2 (vap) are 0.055 and 0.031 cal-1K-1 respectively, then enthalpy of sublimation of iodine at 250° in cal g-1 is:
-
2.85
-
11.4
-
5.7
-
22.8
-
-
10) What is the molar solubility of Al(OH)3 in 0.2 M NaOH solution? Given that, solubility product of Al(OH)3 = 2.4 × 10-24:
-
3 × 10-19
-
12 × 10-21
-
12 × 10-23
-
3 × 10-22
-
-
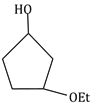
11) The major product of the following reaction is:
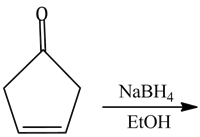
-
-
12) The correct order of atomic radii is:
-
Nd > Ce > Eu > Ho
-
Ho > Nd > Eu > Ce
-
Ce > Eu > Ho > Nd
-
Eu > Ce > Nd > Ho
-
-
13) If p is the momentum of the fastest electron ejected from a metal surface after the irradiation of light having wavelength ? then for (A) 5 p momentum of the photoelectron, the wavelength of the light should be:
(Assume kinetic energy of ejected photoelectron to be very high in comparison to work function)
-
-
14) For the following reactions, equilibrium constant are given:
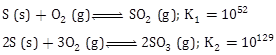
The equilibrium constant for the reaction
2SO2 (g) + O2 (g) ? 2SO3 (g) is:
-
1077
-
1025
-
10181
-
10154
-
-
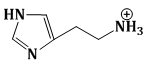
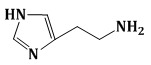
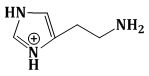
15) The predominant form of histamine present in human blood is (pKa, Histidine = 6.0)
-
-
16) The organic compound that gives following qualitative analysis is:
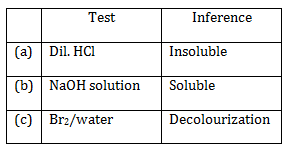
-
-
17) Excessive release of CO2 into the atmosphere results in:
-
formation of smog
-
depletion of ozone
-
global warming
-
polar vortex
-
-
18) The major product of the following reaction is
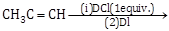
-
CH3CD(I)CHD(CI)
-
CH3C(I)(CI)CHD2
-
CH3CD2CH(CI)(I)
-
CH3CD(CI)CHD(I)
-
-
19) For the reaction of H2 with I2, the rate constant is 2.5 × 10-4 dm3 mol–1 s–1 at 327°C and 1.0 dm3 mol–1 s–1 at 527°C. The activation energy for the reaction, in kJ mol–1 is: (R = 8.314 J K–1 mol–1)
-
72
-
166
-
150
-
59
-
-
20) A hydrated solid X on heating initially gives a monohydrated compound Y. Y upon heating above 373K leads to an anhydrous white powder Z. X and Z, respectively, are:
-
Washing soda and soda ash.
-
Washing soda and dead burnt plaster.
-
Baking soda and dead burnt plaster.
-
Baking soda and soda ash.
-
-
21) Elevation in the boiling point for 1 molal solution of glucose is 2 K. The depression in the freezing point for 2 molal solution of glucose in the same solvent is 2 K. The relation between Kb and Kf is: Kb = ___ Kf
-
22) For the chemical reaction X ? Y, the standard reaction Gibbs energy depends on temperature T (in K) as
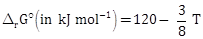
The major component of the reaction mixture at T is X if T = _____ K
-
23) Heat treatment of muscular pain involves radiation of wavelength of about 900 nm. [RH = 1 × 10 5 cm-1, h = 6.6 × 10-34 Js, c = 3 × 108ms-1]
The spectral line of H – atom is suitable of this purpose is Paschen, ? ? ______
-
24) 8 g of NaOH is dissolved in 18 g of H2O. Mole fraction of NaOH in solution is
-
25) The strength of 11.2 volume solution of H2O2 is ____ %
[Given that molar mass of H =1 g mol-1 and O = 16 g mol-1]
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) If the fractional part of the number
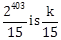 , then k is equal to:
, then k is equal to:-
6
-
8
-
4
-
14
-
-
2) The equation of line passing through (–4, 3, 1), parallel to the plane x + 2y – z – 5 = 0 and intersecting the line
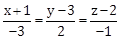 is:
is: -
-
3) If the Boolean expression (p ? q) ? (p ? q) is equivalent to p ? q, where ?, ? ? {?, ?}, then the ordered pair (?, ?)
-
(?, ?)
-
(?, ?)
-
(?, ?)
-
(?, ?)
-
-
4) The curve amongst the family of curves represented by the differential equation, (x2 -y2) dx + 2xy dy = 0 which passes through (1, 1), is:
-
a circle with centre on the x-axis
-
an ellipse with major axis along the y-axis
-
a circle with centre on the y-axis
-
a hyperbola with transverse axis along the x-axis
-
-
5) Let N be the set of natural numbers and two functions f and g be defined as f, g: N?N such that
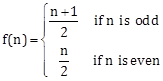
and g(n) = n - (-1)n. Then fog is:
-
onto but not one-one
-
one-one but not onto
-
both one-one and onto
-
neither one-one nor onto
-
-
6) If
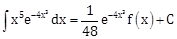 where C is a constant of integration, then f(x) is equal to:
where C is a constant of integration, then f(x) is equal to:-
-2x3 – 1
-
-4x3 – 1
-
-2x3 + 1
-
4x3 + 1
-
-
7) A square is inscribed in the circle x2 +y2 – 6x + 8y – 103 = 0, with its sides parallel to the coordinate axes. Then the distance of a vertex of the square (from the origin) which is nearest to the origin is:
-
6
-
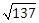
-
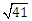
-
13
-
-
8) Let [x] denote the greatest integer less than or equal to x. Then:

-
does not exist
-
equals ?
-
equal ? + 1
-
equals 0
-
-
9) Let a1, a2,…, a10 be a G. P. If
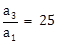 , then
, then 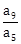 equals:
equals:-
54
-
4(52)
-
53
-
2(52)
-
-
10) If sin4 ? + 4 cos4 ? + 2 = 4
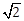 sin ? cos ?; ?, ? ? [0, ?] then cos (? + ?) – cos (? – ?) is equal to:
sin ? cos ?; ?, ? ? [0, ?] then cos (? + ?) – cos (? – ?) is equal to:-
0
-
-1
-
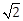
-
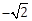
-
-
11) In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then probability that the student has opted neither for NCC nor for NSS is:
-
-
12) 
-
-
13) 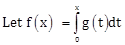 , were g is a non-zero even function. If f(x+5) = g(x), then
, were g is a non-zero even function. If f(x+5) = g(x), then  equals
equals -
-
14) The number of integral values of m for which the equation
(1 + m2) x2 – 2 (1 + 3m) x + (1 + 8m) = 0 has no real root is:
-
infinitely many
-
2
-
3
-
1
-
-
15) Let
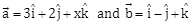 , for some real x. Then
, for some real x. Then 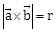 is possible if:
is possible if: -
-
16) The integral
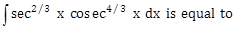 : (Here C is a constant of integration)
: (Here C is a constant of integration)-
3 tan-1/3 x + C x
-
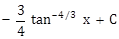
-
-3 cot-1/3 x + C
-
-3 tan-1/3 x + C
-
-
17) Let f (x) = 15 – |x – 10|; x ? R. then the set of all values of x, at which the function, g(x) = f(f(x)) is not differentiable, is:
-
{5, 10, 15}
-
{10}
-
{5, 10, 15, 20}
-
{10, 15}
-
-
18) Slope of a line passing through P(2, 3) and interesting the line, x + y = 7 at a distance of 4 units from P, is:
-
-
19) If the tangent to the curve
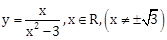 at a point (?, ?) ? (0, 0) on it is parallel to the line 2x + 6y – 11 = 0 then
at a point (?, ?) ? (0, 0) on it is parallel to the line 2x + 6y – 11 = 0 then-
|2? + 6?| = 11
-
|2? + 6?| = 19
-
|6? + 2?| = 19
-
|6? + 2?| = 9
-
-
20) Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is
-
210
-
180
-
170
-
190
-
-
21) Both the means and the standard deviation of 50 observations x1, x2,…..,x50 are equal to 16. If the mean of the observations (x1 – 4)2, (x2 – 4)2, …..,(x50 – 4)2 is p, then
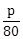 is equal to _______.
is equal to _______. -
22) Let P be the point of intersection of the common tangents to the parabola y2 = 12x and the hyperbola 8x2 – y2 = 8. If S and S' denote the foci of the hyperbola where S lies on the positive x-axis and P divides SS' in a ratio m : n, then (m + n) is equal to _________.
-
23) If
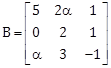 is the inverse of a 3 × 3 matrix A, then the sum of all values of ? for which |A| + 1 = 0, is equal to _____________.
is the inverse of a 3 × 3 matrix A, then the sum of all values of ? for which |A| + 1 = 0, is equal to _____________. -
24) If the volume of parallelepiped formed by the vectors
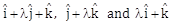 is minimum, then
is minimum, then 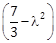 is equal to ________.
is equal to ________. -
25) PQR is a triangular park with PQ = PR = 200m. A T.V. tower stands at the mid-point of QR. If the angles of elevation of the tower at P, Q and R are respectively 45°, 30° and 30°, where we get the height as h m, then
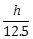 is equal to __________.
is equal to __________.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25