Question Paper (Section wise)
-
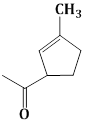
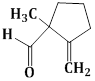
1) 
-
y = x2 + constant
-
y2 = x + constant
-
y2 = x2 + constant
-
xy = constant
-
-
2) Rod of length L at room temperature and uniform area of cross section A, is made of a metal having coefficient if linear expansion α/°C. It is observed that an external compressive force F, is applied on each of its ends, prevents any change in the length of the rod when it temperature rises △TK. Young’s modulus, Y for this metal is
-
-
3) Two masses m and
 are connected at the two ends of a massless rigid rod of length ℓ. The rod is suspended by a thin wire of torsional constant k at the center of mass of the rod-mass system (see figure). Because of torsional constant k, the restoring torque is τ = k θ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be
are connected at the two ends of a massless rigid rod of length ℓ. The rod is suspended by a thin wire of torsional constant k at the center of mass of the rod-mass system (see figure). Because of torsional constant k, the restoring torque is τ = k θ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be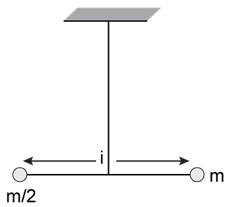
-
-
4) A current of 2 mA was passed through an unknown resistor which dissipated a power of 4.4 W. Dissipated power when an ideal power supply of 11 V is connected across it is:
-
11 × 10-5 W
-
11 × 10-3 W
-
11 × 10-4 W
-
11 × 105 W
-
-
5) The diameter and height of a cylinder are measured by a meter scale to be 12.6 ± 0.1cm and 34.2±0.1cm, respectively. What will be the value of its volume in appropriate significant figures?
-
4264 ± 81cm3
-
4264 ± 81.0cm3
-
V = 4260 ± 80 cm3
-
4300 ± 80cm3
-
-
6) A particle executes simple harmonic motion with an amplitude of 5 cm. When the particle is at 4 cm from the mean position, the magnitude of its velocity is SI units equal to that of its acceleration. Then, its periodic time in seconds is:
-
-
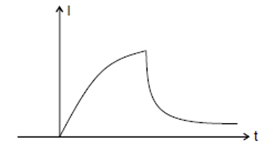
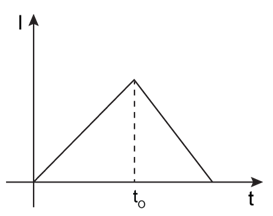
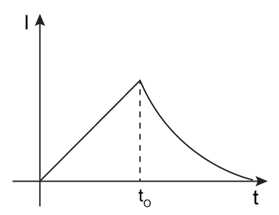
7) In the circuit shown, The switch S1 is close at time t = 0 and the switch S2 is kept open. At some later time (t0), the switch S1 is opened and S2 is closed. The behaviour of the current I as a function of time‘t’ is given by:

-
-
8) An object is at a distance of 20 m from a convex lens of focal length 0.3 m. The lens forms an image of the object. If the object moves away from the lens at a speed of 5 m/s, the speed and direction of the image will be:
-
2.26×10-3 m/s away from the lens
-
0.92×10-3 m/s away from the lens
-
3.22×10-3 m/s towards the lens
-
1.16×10-3 m/s towards the lens
-
-
9) In the figure shown below, the charge on the left plate of the μF Capacitor is -30μC. The charge on the right place of the 6μF capacitor is
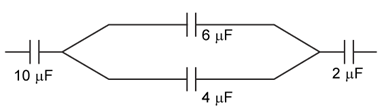
-
-12μC
-
+12μC
-
-18μC
-
+18μC
-
-
10) An alpha-particle of mass m suffers 1-deminisional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is:
-
2 m
-
3.5 m
-
1.5 m
-
4 m
-
-
11) In the given circuit diagram, the currents, I1 = -0.3 A, I4 = 0.8 A and I5 = 0.4 A, are flowing as shown. The currents I2, I3 and I6, respectively are:
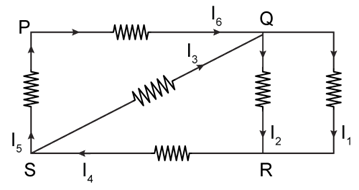
-
1.1 A, -0.4 A, 0.4A
-
1.1 A, 0.4 A, 0.4A
-
0.4 A, 1.1 A, 0.4A
-
-0.4 A, 0.4 A, 0.4A
-
-
12) A simple harmonic motion is represented by:
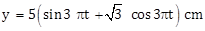
The amplitude and time period of the motion are:
-
-
13) A cell of internal resistance r drives current through an external resistance R. The power delivered by the cell to the external resistance will be maximum when:
-
R = 0.001 r
-
R = 1000 r
-
R = 2r
-
R = r
-
-
14) The magnetic field of an electromagnetic wave is given by:
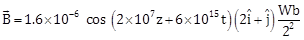
The associated electric field will be:
-
-
15) Calculated the limit of resolution of a telescope objective having a diameter of 200 cm, if it has to detect light of wavelenght 500 nm coming from a star.
-
457.5 × 10-9 radian
-
610 × 10-9radian
-
305 × 10-9 radian
-
152.5 × 10-9 radian
-
-
16) If ‘M’ is the mass of water that rises in a capillary tube of radius ‘r’, then mass of water which will rise in a capillary tube of radius ‘2r’ is:
-
4 M
-
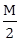
-
M
-
2 M
-
-
17) For a given gas at 1 atm pressure, rms speed of the molecules is 200 m/s at 127°C. At 2 atm pressure and at 227°C, the rms speed of the molecules will be:
-
80 m/s
-
80
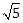 m/s
m/s -
100 m/s
-
100
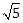 m/s
m/s
-
-
18) A solid sphere of mass ‘M’ and radius ‘a’ is surrounded by a uniform concentric spherical shell of thickness 2a and mass 2M. The gravitational field at distance ‘3a’ from the centre will be:
-
-
19) The magnitude of the magnetic field at the centre of an equilateral triangular loop of side 1 m which is carrying a current of 10 A is: [Take µ0 = 4π × 10-7 NA-2]
-
9µ T
-
1µ T
-
3µ T
-
18µ T
-
-
20) The graph shows how the magnification m produced by a thin lens varies with image distance v. What is the focal length of the lens used?

-
-
21) A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. If this square loop is changed to a circular loop and it carries the same current, the magnitude of the magnetic diploe moment of circular loop will be ______×

-
22) A galvanometer of resistance 100 Ω has 50 division on its scale and has sensitivity of 20 µ A/ division. It is to be converted to a voltmeter with three ranges, of 0-2 V, 0-10 V and 0-20 V. For the given case the closed value of total resistance when connected in series is ______ kΩ.
-
23) For the given circuit what will be the output for logic gate when both input A & B are 1 (high)?
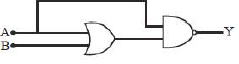
-
24) A damped harmonic oscillator has a frequency of 5 oscillations per seconds. The amplitude drops to half its value for every 10 oscillations. The time it will take to drop to
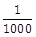 of the original amplitude is closed to _______ sec.
of the original amplitude is closed to _______ sec. -
25) The election field in a region is given by
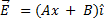 where E is in NC-1 and x in meters. The values of constants are A = 20 SI unit and B = 10 SI unit. If the potential at x = = 1 is V1 and that at x= -5 is V2 then V1 – V2 is ______ V.
where E is in NC-1 and x in meters. The values of constants are A = 20 SI unit and B = 10 SI unit. If the potential at x = = 1 is V1 and that at x= -5 is V2 then V1 – V2 is ______ V.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) The correct decreasing order for acidic strength is
-
NO2CH2COOH > FCH2COOH > CNCH2COOH > CICH2COOH
-
FCH2COOH > NCCH2COOH > NO0CH2COOH > CICH2COOH
-
CNCH2COOH > O2NCH2COOH > FCH2COOH > CICH2COOH
-
NO2CH2COOH > NCCH2COOH > FCH2COOH > CICH2COOH
-
-
2) Number of stereo centers present in linear and cyclic structures of glucose are respectively
-
4 & 5
-
5 & 5
-
4 & 4
-
5 & 4
-
-
3) For emission line of atomic hydrogen from n1= 8 to nf = n, the plot of wave number
 against
against 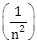 will be (The Rydberg constant, RH is in wave number unit)
will be (The Rydberg constant, RH is in wave number unit)-
Linear with intercept – RH
-
Non linear
-
Linear with slope RH
-
Linear with slope – RH
-
-
4) An organic compound ‘A’ is oxidised with Na2O2 followed by boiling with HNO3. The resultant solution is then treated with ammonium molybdate to yield a yellow precipitate. Based on above observation, the element present in the given compound is:
-
Phosphorus
-
Sulphur
-
Nitrogen
-
Fluorine
-
-
5) The reaction that is NOT involved in the ozone layer depletion mechanism in the stratosphere is:
-

-

-
CH4 + 2O3 ⟶ 3CH2 = o + 3H2O
-
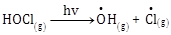
-
-
6) The electrolytes usually used in the electroplating of gold and silver, respectively, are:
-
[Au(CN)2]- and [Ag(CN)2]-
-
[Au(CN)2]- and [AgCl2]-
-
[Au(OH)4]- and [Ag(OH)2]-
-
[Au(NH3)2]+ and [Ag(CN)2]-
-
-
7) For the cell
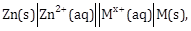 different half cells and their standard electrode potentials are given below:
different half cells and their standard electrode potentials are given below: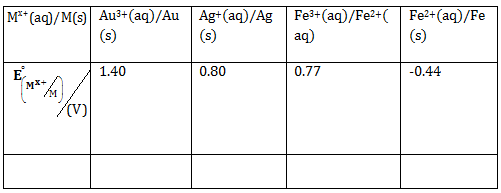
If
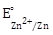 = −0.76 V, Which cathode will give a maximum value of E⁰cell per electron transferred?
= −0.76 V, Which cathode will give a maximum value of E⁰cell per electron transferred? -
Ag+ / Ag
-
Fe3 +/Fe2+
-
Au3 + /Au
-
Fe2+ / Fe
-
-
8) The amphoteric hydroxide is:
-
Be(OH)2
-
Ca(OH)2
-
Mg(OH)2
-
Sr(OH)2
-
-
9) Match the ores (column A) with the metals (column B)
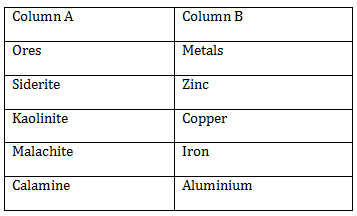
-
I – a, II – b, III – c, IV - d
-
I – c, II – d, III – b, IV - a
-
I –c, II – d, III – a, IV - b
-
I – b, II – c, III – d, IV - a
-
-
10) Chlorine on reaction with hot and concentrated sodium hydroxide gives:
-
Cl- and ClO3-
-
Cl- and ClO-
-
ClO3- and ClO2-
-
Cl- and ClO2-
-
-
11) The element that shows greater ability to form pπ - pπ multiple bonds, is:
-
Sn
-
C
-
Ge
-
Si
-
-
12) Glucose and Galactose are having identical configuration in all the positions except position.
-
C – 4
-
C – 3
-
C – 5
-
C – 2
-
-
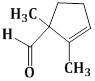
13) The major product obtained in the following reaction is:
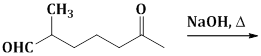
-
-
14) The increasing order of basicity of the following compounds is:




-
(d) < (b) < (a) < (c)
-
(a) < (b) < (c) < (d)
-
(b) < (a) < (c) < (d)
-
(b) < (a) < (d) < (c)
-
-
15) For the solution of the gases w, x, y and z in water at 298 K, the Henrys law constants (KH) are 0.5, 2 35 and 40 kbar, respectively. The correct plot for the given data is:
-
-
16) The ore that contains the metal in the form of fluoride is:
-
saphalerite
-
malachite
-
magnetite
-
cryolite
-
-
17) For any given series of spectral lines of atomic hydrogen, let ∆⊽ = |∆⊽max - ∆⊽min| difference in maximum and minimum frequencies in cm-1. the ration ∆⊽Lymann / ∆⊽Balmer
-
5 : 4
-
4 : 1
-
9 : 4
-
27 :5
-
-
18) C60, an allotrope of carbon contains:
-
20 hexagons and 12 pentagons.
-
12 hexagons and 20 pentagons.
-
18 hexagons and 14 pentagons.
-
16 hexagons and 16 pentagons.
-
-
19) The correct match between Item-I and Item-II is:
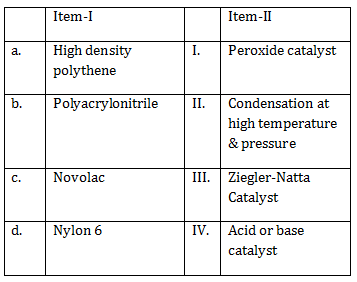
-
a → III, b → I, c → II, d → IV
-
a → IV, b → II, c → I, d → III
-
a → II, b → IV. c → I, d → III
-
a → III, b → I, c → IV, d → II
-
-
20) The crystal field stabilization energy (CFSE) of [Fe(H2O)6]Cl2 and K2[NiCl4], respectively, are :-
-
–0.4∆o and –0.8∆t
-
–0.4∆o and –1.2∆t
-
–2.4∆o and –1.2∆t
-
–0.6∆o and –0.8∆t
-
-
21) 20 mL of 0.1 M H2SO4 is added to 30 mL of 0.2 M NH4OH solution. The pH of the resultant mixture is [pkb of NH4OH = 4.7]
-
22) 5.1 g NH4SH is introduced in 3.0 L evacuated flask at 327°C. 30% of the solid NH4 SH decomposed to NH3 and H2S as gases. The Kp in atm2 of the reaction at 327°C is
(R = 0.082 L atm mol-1 k -1, Molar mass of S = 32g mol-1, molar mass of N = 14g mol-1)
-
23) If the de Brogile wavelength of the electron in nth Bohr orbit in a hydrogenic atom is equal to 1.5πa0 (a0 is Bohr radius), then the value of n/z is:
-
24) The calculated spin only magnetic moments (BM) of the cationic species of
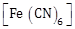 is
is -
25) The mole fraction of a solvent in aqueous solution of a solute is 0.8. The molality (in mol kg-1) of the aqueous solution is
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) Consider the set of all lines px + qy + r = 0 such that 3p + 2q + 4r = 0. Which one of the following statements is true?
-
The lines are concurrent at the point
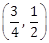
-
Each line passes through the origin
-
The lines are all parallel
-
The lines are not concurrent
-
-
2) For any
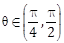 , the expression 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4 sin6θ equals:
, the expression 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4 sin6θ equals:-
13 – 4cos2θ + 6 sin2 θcos2θ
-
13 – 4 cos6 θ
-
13 – 4cos2θ + 6cos4θ
-
13 – 4 cos4θ + 2sin2cos2θ
-
-
3) Let f : R → R be a function defined as
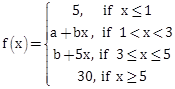
Then f is:
-
continuous if a = 5 and b = 5
-
continuous if a = 5 and b = 10
-
continuous if a = 0 and b = 5
-
not continuous for any values of a and b
-
-
4) If the area of an equilateral triangle inscribed in the circle, x2 + y2 + 10x + 12y + c = 0 is 27
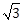 sq. units then c is equal to:
sq. units then c is equal to:-
13
-
20
-
-25
-
25
-
-
5) The value of cot
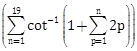 is:
is: -
-
6) With the usual notation, in ∆ABC, if ∠A + ∠B = 120°,
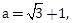
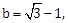 then the ratio ∠A : ∠B, is:
then the ratio ∠A : ∠B, is:-
7:1
-
5:3
-
9:7
-
3:1
-
-
7) The value of the integral
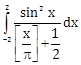 (where [x] denotes the greatest integer less than or equal to x) is:
(where [x] denotes the greatest integer less than or equal to x) is:-
0
-
sin 4
-
4
-
4 – sin 4
-
-
8) The sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of items is
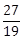 . Then the common ratio of this series is:
. Then the common ratio of this series is: -
-
9) Equation of a common tangent to the parabola y2 = 4x and the hyperbola xy = 2 is:
-
x + y + 1 = 0
-
x – 2y + 4 = 0
-
x + 2y + 4 = 0
-
4x + 2y + 1 = 0
-
-
10) If a curve passes through the point (1, -2) and has slope of the tangent at any point (x, y) on it as
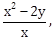 then the curve also passes through the point:
then the curve also passes through the point:-
(3, 0)
-
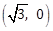
-
(-1, 2)
-
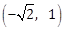
-
-
11) The mean and the variance of five observations are 4 and 5.20, respectively. If three of the observations are 3, 4 and 4; then the absolute value of the difference of the other two observations, is:
-
7
-
5
-
1
-
3
-
-
12) Let S and S’ be the foci of an ellipse and B be any one of the extremities of its minor axis. If ΔS’BS is a right angled triangle with right angle B and area (ΔS’BS) = 8 sq. units, then the length of a latus rectum of the ellipse is:
-
4
-
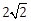
-
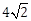
-
2
-
-
13) Given that the slope of the tangent to a curve y = y(x) at any point (x, y) is
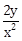 . If the curve passes through the center of the circle x2 + y2 - 2x - 2y = 0, then its equation is:
. If the curve passes through the center of the circle x2 + y2 - 2x - 2y = 0, then its equation is:-
x loge |y| = x – 1
-
x loge |y| = –2 (x – 1)
-
x2 loge |y|= –2 (x – 1)
-
x loge |y|= 2(x – 1)
-
-
14) If the eccentricity of the standard hyperbola passing through the point (4, 6) is 2, then the equation of the tangent to the hyperbola at (4, 6) is:
-
2x – 3y + 10 = 0
-
x – 2y + 8 = 0
-
2x – y – 2 = 0
-
3x – 2y = 0
-
-
15) If
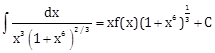 where C is a constant of integration, then the function f(x) is equal to:
where C is a constant of integration, then the function f(x) is equal to: -
-
16) If the tangent to the curve, y = x3 + ax – b at the point (1, -5) is perpendicular to the line, -x + y + 4 = 0, then which one of the following points lies on the curve?
-
(2, -2)
-
(-2, 2)
-
(-2, 1)
-
(2, -1)
-
-
17) If the line
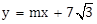 is normal to the hyperbola
is normal to the hyperbola 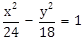 , then the value of m is:
, then the value of m is: -
-
18) Let
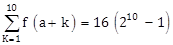 , where the function f satisfies f(x + y) = f(x)f(y) for all natural numbers x, y and f (1) = 2. Then the natural number ‘a’ is:
, where the function f satisfies f(x + y) = f(x)f(y) for all natural numbers x, y and f (1) = 2. Then the natural number ‘a’ is:-
4
-
16
-
2
-
3
-
-
19) If
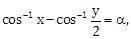 where
where 
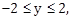 and
and 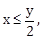 then for all x, y, 4x2 – 4xy cos α + y2 is equal to:
then for all x, y, 4x2 – 4xy cos α + y2 is equal to:-
4 sin2α – 2x2y2
-
4 cos2 α + 2x2y2
-
2 sin2 α
-
4 sin2 α
-
-
20) A spherical iron ball of radius 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm2/min. When the thickness of the ice is 5 cm, then the rate at which the thickness (in cm/min) of ice decreases is:
-
-
21) If z and w are two complex numbers such that
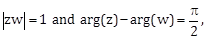 then
then 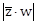 is equal to ___________.
is equal to ___________. -
22) If the number of ways of choosing 10 objects out of 31 objects of which 10 are identical and the remaining 21 are distinct, is 2m, then m is equal to ______________.
-
23) The value of p such that
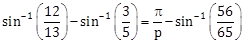 , is equal to _____________.
, is equal to _____________. -
24) If the line
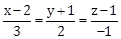 intersects the plane 2x + 3y – z + 13 = 0 at a point P and the plane 3x + y + 4z = 16 at a point Q, then (PQ)2 is equal to ________________.
intersects the plane 2x + 3y – z + 13 = 0 at a point P and the plane 3x + y + 4z = 16 at a point Q, then (PQ)2 is equal to ________________. -
25) Let g(x) = cos x2, f(x) =
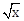 , and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 =0. If the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α , x = β and y = 0, is
, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 =0. If the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α , x = β and y = 0, is  then (a + b) is equal to _____________.
then (a + b) is equal to _____________.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25