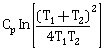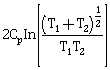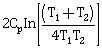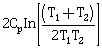Question Paper (Section wise)
-
1) Surface of certain metal is first illuminated with light of wavelength λ1 = 350 nm and then, the light of wavelength λ2 = 540 nm. It is found that the maximum speed of the photo electrons in the two cases differ by a factor of 2. The work function of the metal (in eV) is close to:
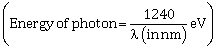
-
1.8
-
2.5
-
5.6
-
1.4
-
-
2) A sample of radioactive material A, that has an activity of 10mCi (1 Ci = 3.7 × 1010 decays/s), has twice the number of nuclei as another sample of different radioactive material B which has an activity of 20mCi. The correct choice for half-lives of A and B would then be respectively:
-
5 days and 10 days
-
10 days 40 days
-
20 days 5 days
-
20 days 10 days
-
-
3) Three blocks A, B and C are lying in a smooth horizontal surface, as shown in the figure. A and B have equal masses, m while C has mass M. Block A is given an initial speed v towards B due to which it collides with B perfectly inelastically. The combined mass collides with C, also perfectly inelastically. The combined mass collides with C, also perfectly inelastically if
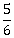 th of the initial kinetic energy is lost in whole process. What is value of M/m?
th of the initial kinetic energy is lost in whole process. What is value of M/m?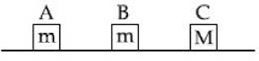
-
5
-
2
-
4
-
3
-
-
4) A metal plate of area 1 × 10-4 m2 is illuminated by a radiation of intensity 16 mW/m2. The work function of the metal is 5 eV. The energy of the incident photons is 10 eV and only 10 % of it produces photo electrons. The number of emitted photo electrons per second and their maximum energy, respectively, will be:
[1eV = 1.6 ×1019J]
-
1014 and 10 eV
-
1012 and 5 eV
-
1011 and 5 eV
-
1010 and 5 eV
-
-
5) The modulation frequency of an AM radio station is 250 kHz, which is 10% of the carrier wave. If another AM station approaches you for license what broadcast frequency will you allot?
-
2750kHz
-
2900kHz
-
2250 kHz
-
2000kHz
-
-
6) Two force P and Q, of magnitude 2F and 3F, respectively, are at an angle θ with each other. If the force Q is doubled, then resultant also doubled. Then, the angle θ is:
-
120°
-
60°
-
90°
-
30°
-
-
7) In a Young’s double slit experiment, the path difference, at a certain point on the screen, between two interfering waves is 1/8th of wavelength. The ratio of the intensity at this point to that at the Centre of a bright fringe is close to:
-
0.74
-
0.85
-
0.94
-
0.80
-
-
8) A slab is subjected to the two forces
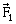 and
and of same magnitude F as shown in the figure. Force
of same magnitude F as shown in the figure. Force  is in XY –plane while force F1 acts along Z- axis at the point
is in XY –plane while force F1 acts along Z- axis at the point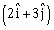 . The moment of these forces about point O will be:
. The moment of these forces about point O will be: -
-
9) In a Wheatstone bridge (see figure) Resistance P and Q are approximately equal. When R = 400 Ω, the bridge is balanced. On interchanging P and Q, the value of R, for balance is 405 Ω. The value of X is close to:
-
401.5 ohm
-
404.5 ohm
-
403.5 ohm
-
402.5 ohm
-
-
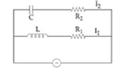
10) In the above circuit,.

Current in L-R1 path is I1 and C- R2 path is I2. The voltage of A. C. source is given by,
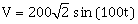 volts.
volts.The phase difference between I1 and I2 is:
-
60°
-
30°
-
90°
-
150°
-
-
11) A galvanometer, whose resistance is 50 ohm, has 25 divisions in it. When a current of 4 × 10-4 A passes through it, its needle (pointer) deflects by one division. To use this galvanometer as a voltmeter of range 2.5 V, it should be connected to a resistance of:
-
250 ohm
-
200 ohm
-
6200 ohm
-
6250 ohm
-
-
12) The charge on a capacitor plate in a circuit, as a function of time, is shown in the figure:
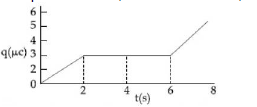
What is the value of current at t = 4 s?
-
Zero
-
3 µA
-
2 µA
-
1.5 µA
-
-
13) Young’s moduli of two wires A and B are in the ration 7:4 Wire A is 2 m long and has radius R. Wire A is 2 m long and has radius r. Wire B is 1.5 m long and has radius 2 mm. If the two wires stretch by the same length for a given load, then the value of R is closed to:
-
1.3 mm
-
1.5 mm
-
1.7 mm
-
1.9 mm
-
-
14) A body of mass m1 moving with an unknown velocity of
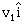 undergoes a collinear collision with a body of mass m2 moving with a velocity
undergoes a collinear collision with a body of mass m2 moving with a velocity  After collision m1 and m2 move with velocities of
After collision m1 and m2 move with velocities of 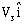 and
and 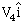 respectively.
respectively.-
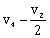
-
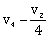
-
V4 – V2
-
V4 + V2
-
-
15) A rocket has to be launched from each in such a way that it never returns. If E is the minimum energy delivered by the rocket launcher, what should be the minimum energy that the launcher should have if the same rocket is to be launched form the surface of the moon? Assume that the density of the earth and the moon are equal and that the earth’s volume is 64 times the volume of the moon.
-
-
16) The total number of turns and cross-section area in solenoid is fixed. However, its length L is varied by adjusting the separation between windings. The inductance of solenoid will be proportional to:
-
1/L
-
L
-
1/L2
-
L2
-
-
17) Determine the charge on the capacitor in the following circuit:
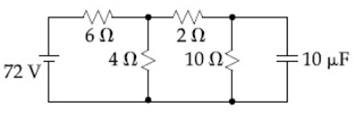
-
200μC
-
60μC
-
10μC
-
2μC
-
-
18) A rigid square loop of side ‘a’ and carrying current I2 is laying on a horizontal surface near a long current I1 wire in the same plane as shown in figure. The net force on the loop due to the wire will be:

-
Repulsive and equal to
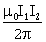
-
Attractive and equal to
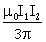
-
Zero
-
Repulsive and equal to
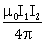
-
-
19) The elastic limit of brass is 379 MPa. What should be the minimum diameter of a brass rod if it is to support a 400 N load without exceeding its elastic limit?
-
1.00 mm
-
1.16 mm
-
0.90 mm
-
1.36 mm
-
-
20) Water from a tap emerges vertically downwards with an initial speed of 1.0 ms-1. The cross-sectional area of the tap is 10-4m2. Assume that the pressure is constant throughout the stream of water and that flow is streamlined. The cross-sectional area of the stream, 0.15 m below the tap would be:
(Take, g = 110 ms-2)
-
5 × 10-4 m2
-
5 × 10-5 m2
-
1 × 10-5 m2
-
2 × 10-5 m2
-
-
21) A cubical block of side 0.5 m floats on water with 30% of its volume under water. What is the maximum weight (kg) that can be put on the block without fully submerging it under water?
[Take density of water = 103 kg/m3]
-
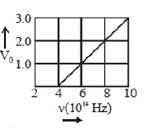
22) The stopping potential V0 (in volt) as a function of frequency (ν) for a sodium emitter, is shown in the figure. The approximate work function of sodium, from the data plotted in the figure, will be _______ eV.
(Given: Planck’s constant (h) = 6.63 × 10-34 Js, electron charge e = 1.6 × 10-19 C)
-
23) A submarine (A) travelling at 18 km/hr is being chased along the line of its velocity by another submarine (B) travelling at 27 km/hr. B sends a sonar signal of 500 Hz to detect A and receives a reflected sound of frequency ν. The value of v is close to ________ Hz.
(Speed of sound in water = 1500 ms-1)
-
24) The reading of the ammeter (in mA) for a silicon diode in the given circuit is
-
25) A convex lens (of focal length 20 cm) and a concave mirror, having their principal axes along the same lines, are kept 80 cm apart from each other. The concave mirror is to the right of the convex lens. When an object is kept at a distance of 30 cm to the left of the convex lens, its image remains at same position even if the concave mirror, by itself would produce a virtual image would be _______ cm.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) The group number, number of valence electrons and valency of an element with atomic number 15, respectively, are:
-
15, 5 and 3
-
15, 6 and 2
-
16, 5 and 2
-
16, 6 and 3
-
-
2) The correct match between Item-I and Item-II is:

-
a → r, b → p, c → s, d → q
-
a → q, b → s, c → p, d → r
-
a → r, b → s, c → p, d → q
-
a → q, b → p, c → s, d → r
-
-
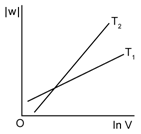
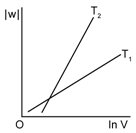
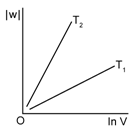
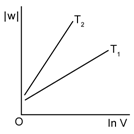
3) Consider the reversible isothermal expansion of an ideal gas in closed system at two different temperatures T1 & T2 (T1 < T2). The correct graphical depiction of the dependence of work done (w) on the final volume (v).
-
-
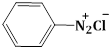
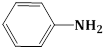
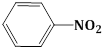
4) The increasing order of the pKb of the following compound is:
(A)

(B)

(C)
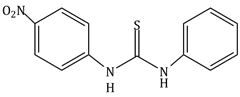
(D)
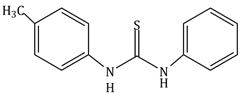
-
(c) < (a) < (d) < (b)
-
(b) < (d) < (a) < (c)
-
(a) < (c) < (d) < (b)
-
(b) < (d) < (c) < (a)
-
-
5) Which of the following tests cannot be used for identifying amino acids?
-
Biuret test
-
Barfoed test
-
Ninhydrin test
-
Xanthoproteic test
-
-
6) The difference in the number of unpaired electrons of a metal ion in its high-spin and low-spin octahedral complexes is two. The metal ion is:
-
Ni2+
-
Fe2+
-
Co2+
-
Mn2+
-
-
7) NaH is an example of :
-
electron rich hydride
-
metallic hydride
-
saline hydride
-
molecular hydride
-
-
8) Peroxyacetyl nitrate (PAN), an eye irritant is produced by:
-
classical smog
-
acid rain
-
organic waste
-
photochemical smog
-
-
9) Two blocks of the same metal having same mass and at temperature T1 and T2 respectively, are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure. The change in entropy, ΔS, for this process is:
-
-
10) Which of the following compounds will be suitable for Kjeldahl‘s method for nitrogen estimation?
-
-
11) Given:
i. C(graphite)+O2(g) → CO2(g); ∆rH°= x kJ mol-1
ii. C(graphite)+
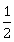 O2(g) → CO(g); ∆rH° = y kJ mol-1
O2(g) → CO(g); ∆rH° = y kJ mol-1iii. CO(g)+
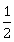 O2(g) → CO2(g); ∆rH°= z kJ mol-1
O2(g) → CO2(g); ∆rH°= z kJ mol-1Based on the above thermochemical equations, find out which one of the following algebraic relationships is correct?
-
x = y + z
-
z = x – y
-
y = 2z –x
-
x = y – z
-
-
12) The major product of the following reaction is:
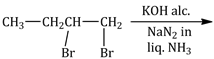
-
CH3CH = C = CH2
-
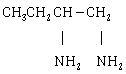
-
CH3 CH=CHCH2NH2
-
CH 3CH2 C ≡ CH
-
-
13) The statement that is INCORRECT about the interstitial compound is:
-
they have metallic conductivity
-
they have high melting points
-
they are chemically reactive
-
they are very hard
-
-
14) The IUPAC symbol for the element with atomic number 119 would be:
-
Uun
-
Uue
-
Unh
-
Une
-
-
15) Polysubsititution is a major drawback in:
-
Friedel Craft’s alkyation
-
Reimer Tiemann reaction
-
Acetylation of aniline
-
Friedel Craft’s acylation
-
-
16) Liquid ‘M’ and liquid ‘N’ form an ideal solution. The vapour pressures of pure liquids ‘M’ and ‘N’ are 450 and 700 mm Hg, respectively at the same temperature. Then correct statement is:
(xM = mole fraction of ‘M’ in solution; xN = mole fraction of ‘N’ in solution;
ym = mole fraction of ‘M’ in vapour phase; yN = mole fraction of ‘M’ in vapour phase)
-
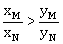
-
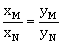
-
(xM-yM) < (xN-yN)
-
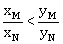
-
-
17) The element having greatest difference between its first and second ionisation energies, is
-
Ca
-
K
-
Ba
-
Sc
-
-
18) Match the catalysis (Column – I) with products (Column –II)
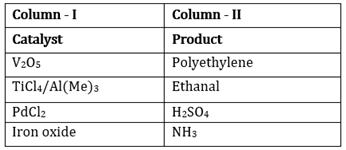
-
(a)-(iii); (b)-(iv); (c)-(i); (d)-(ii)
-
(a)-(iv); (b)-(iii); (c)-(ii); (d)-(i)
-
(a)-(ii); (b)-(iii); (c)-(i); (d)-(iv)
-
(a)-(iii); (b)-(i); (c)-(ii); (d)-(iv)
-
-
19) The INCORRECT statement is:
-
The spin-only magnetic moments of [Fe(H2O)6]2+ and [Cr(H2O)6]2+ are nearly similar.
-
the spin-only magnetic moment of [Ni(NH3)4(H2O)2]2+ is 2.83 BM.
-
The gemstone, ruby, has Cr3+ ions occupying the octahedral sites of beryl.
-
the color of [CoCl(NH3)5]2+ is violet as it absorbs the yellow light
-
-
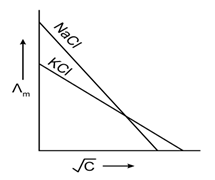
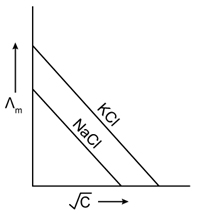
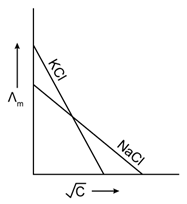
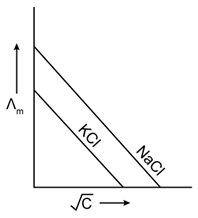
20) Which one of the following graphs between molar conductivity (˄m) versus
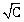 is correct?
is correct? -
-
21) The highest value of the calculate spin-only magnetic moment (in BM) among all the transition metal complexes is
-
22) The ground state energy of hydrogen atom is -13.6 eV. The energy of second excited state of He+ ion in eV is:
-
23) 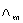 for NaCl, HCl and NaA are 126.4, 425.9 and 100.5 S cm2 mol-1, respectively. If the conductivity of 0.001 MHA is 5 10-5S cm-1, degree of dissociation of HA is:
for NaCl, HCl and NaA are 126.4, 425.9 and 100.5 S cm2 mol-1, respectively. If the conductivity of 0.001 MHA is 5 10-5S cm-1, degree of dissociation of HA is: -
24) The number of pentagons in C60 and trigons (triangles) in white phosphorus, respectively, are 12 and _____
-
25) The basic structural unit of feldspar, zeolites, mica, and asbestos is (SiO4)x hence x is
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) Let
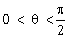 . If the eccentricity of the hyperbola
. If the eccentricity of the hyperbola 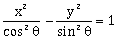 is greater than 2, then the length of its latus rectum lies in the interval:
is greater than 2, then the length of its latus rectum lies in the interval:-
(3, ∞)
-
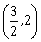
-
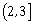
-
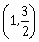
-
-
2) If θ denotes the acute angle between the curves, y = 10 - x2 and y = 2 + x2 at a point of their intersection, then |tan θ| is equal to:
-
-
3) Two cards are drawn successively with replacement from a well shuffled deck of 52 cards. Let X denote the random variable of number of aces obtained in the two drawn cards. Then P(X = 1) + P(X = 2) equals
-
-
4) Two sides of a parallelogram are along the lines, x + y = 3 and x – y + 3 = 0. If its diagonals intersect at (2, 4), then one of its vertex is:
-
(3, 5)
-
(2, 1)
-
(2, 6)
-
(3, 6)
-
-
5) Let f be a differential function such that
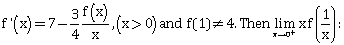
-
exists and equals

-
exists and equals 4
-
does not exist
-
exists and equals 0
-
-
6) On which of the following lines lies the point of intersection of the line,
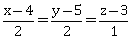 and the plane, x + y + z = 2?
and the plane, x + y + z = 2? -
-
7) Two integers are selected at random from the test set {1, 2, … , 11}. Given that the sum of selected numbers is even, the conditional probability that both the numbers are even is:
-
-
8) If
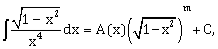 for a suitable chosen integer m and a function A (x), where C is a constant of integration, then (A(x))m equals:
for a suitable chosen integer m and a function A (x), where C is a constant of integration, then (A(x))m equals: -
-
9) Let
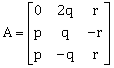 . If AAT = I3, then |p| is:
. If AAT = I3, then |p| is: -
-
10) The integral
 loge x dx is equal to:
loge x dx is equal to: -
-
11) The equation of a tangent to the parabola, x2 = 8y, which makes an angle θ with the positive direction of X-axis, is:
-
y = x tan θ + 2 cot θ
-
y = x tan θ – 2 cot θ
-
x = y cot θ + 2 tan θ
-
x = y cot θ – 2 tan θ
-
-
12) The number of integral values of m for which the quadratic expression, (1+2m)x2 -2(1 + 3m)x + 4 (1 + m), x ⋴ R, is always positive, is:
-
3
-
8
-
7
-
6
-
-
13) A student score the following marks in five tests: 45, 54, 41, 57, 43. His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is:
-
-
14) The vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0 is:
-
-
15) The height of a right circular cylinder of maximum volume inscribed in a sphere of radius 3 is:
-
-
16) Let p, q ϵ R, if
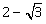 is a root of the quadratic equation, x2 + px + q = 0, then:
is a root of the quadratic equation, x2 + px + q = 0, then:-
q2 + 4p + 14 = 0
-
p2 – 4q + 12 = 0
-
p2 - 4q - 12 = 0
-
q2 - 4p - 16 = 0
-
-
17) If
 then the inverse of
then the inverse of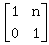 is:
is: -
-
18) Let S be the set of all values of x for which the tangent to the curve y = f (x) = x3 – x2 – 2x at (x, y) is parallel to the line segment joining the points (1, f (1)) and (-1, f (-1)), then S is equal to:
-
-
19) Let f(x) = loge (sin x), (0 < x < π) and g(x) = sin-1(e-x), (x≥0)If α is a positive real number such that a = (fog)’(α) and b = (fog)(α), then
-
aα2 + bα – a = 2α2
-
aα2 – bα – a = 0
-
aα2 – bα – a = 1
-
aα2 + bα + a = 0
-
-
20) A perpendicular is drawn from a point on the line
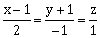 to the plane x + y + z = 3 such that the foot of the perpendicular Q also lies on the plane x – y + z = 3. Then the co-ordinates of Q are
to the plane x + y + z = 3 such that the foot of the perpendicular Q also lies on the plane x – y + z = 3. Then the co-ordinates of Q are-
(2, 0, 1)
-
(-1, 0, 4)
-
(1, 0, 2)
-
(4, 0, -1)
-
-
21) Minimum number of times a fair coin must be tossed so that the probability of getting at least one head is more than 99% is equal to __________.
-
22) The equation
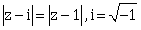 , represents the line through the origin with slope _____________.
, represents the line through the origin with slope _____________. -
23) If the normal to the ellipse 3x2 + 4y2 = 12 at a point P on it is parallel to the line, 2x + y = 4 and the tangent to the ellipse at P passes through Q(4, 4) such that PQ =
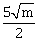 then m is equal to ________.
then m is equal to ________. -
24) If
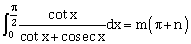 , then –2mn is equal to :
, then –2mn is equal to : -
25) L1 is the line of intersection of the planes 2x – 2y + 3z – 2 = 0, x – y + z + 1 = 0 and L2 is the line of intersection of the planes x + 2y – z – 3 = 0, 3x – y + 2z – 1 = 0. If the distance of the origin from the plane, containing the lines L1 and L2, is
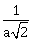 then ‘a’ is equal to _______.
then ‘a’ is equal to _______.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25