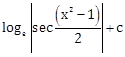Question Paper (Section wise)
-
1) Drift speed of electrons, when 1.5 of current flows in a copper wire of cross section 5 mm2, is v. If the electrons density in copper is 9 × 1028 /m3 the value of v in mm/s is close to (Take charge of electron to be = 1.6 × 10-19 C)
-
0.02
-
3
-
2
-
0.2
-
-
2) An infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is and distance of its centre from the wire is d (d >> a). If the loop applies a force F on the wire then:

-
F = 0
-
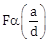
-
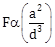
-
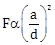
-
-
3) A bar magnet is demagnetized by inserting it inside a solenoid of length 0.2 m, 100 turns, and carrying a current of 5.2 A. The coercivity of the bar magnet is
-
285 A/m
-
2600 A/m
-
520 A/m
-
1200 A/m
-
-
4) At some location on earth the horizontal component of Earth’s magnetic field is 18 × 10-6 T. At this location, magnetic needle of length 0.12 m and pole strength 1.8 A m is suspended from its mid-point using a thread, it makes 45° angle with horizontal in equilibrium. To keep this needle horizontal, the vertical force that should be applied at one of its ends is:
-
3.6 × 10-5 N
-
1.8 × 10-5N
-
1.3 × 10-5 N
-
6.5 × 10-5 N
-
-
5) Two stars of masses 3 × 1031 kg each, and at distance 2 × 1011 m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star’s rotation plane. In order to escape from the gravitation field of this double star the minimum speed that meteorite should have at O is: (Take Gravitational constant G = 6.67 × 10-11Nm2).
-
2.4 × 104m/s
-
1.4 × 105m/s
-
3.8 × 104 m/s
-
2.8 × 105m/s
-
-
6) A particle starts form the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respects to time is shown in figure. What is the position of the particle at time t = 5s?

-
10 m
-
6 m
-
3 m
-
9 m
-
-
7) Three charges Q, +q and +q are placed at the vertices of a right – angle isosceles triangle as shown below. The net electrostatic energy of the configuration is zero, if the value of Q is:

-
+q
-

-
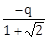
-
-2q
-
-
8) Two equal resistances when connected in series to a battery, consume electric power of 60 W. If these resistances are now connected in parallel combination to the same battery, the electric power consumed will be.
-
60 W
-
240 W
-
120 W
-
30 W
-
-
9) A rigid diatomic ideal gas undergoes an adiabatic process at room temperature. The rational between temperature and volume for the process is TVx = constant, then x is:
-
3/5
-
2/5
-
2/3
-
5/3
-
-
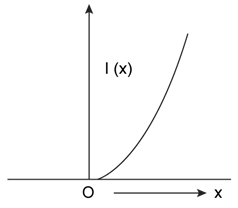
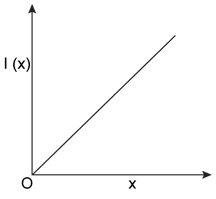
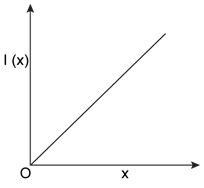
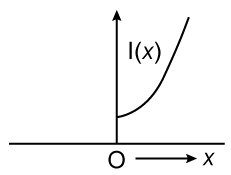
10) The moment if inertia of a solid sphere, about an axis parallel to its diameter and at a distance of x from it, is ‘I(x)’. Which one of the graphs represents the variation of l(x) with x correctly?
-
-
11) Let l, r, c and v represent inductance, resistance, capacitance and voltage, respectively. The dimension of
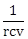 in SI units will be:
in SI units will be:-
[LA-2]
-
[A-1]
-
[LTA]
-
[LT2]
-
-
12) A parallel plate capacitor with plates of area 1 m2 each, are at a separation of 0.1 m. If the electric field between the plates is 100 N/C, the magnitude of charge on each plate is:
-
7.85 × 10-10C
-
6.85 × 10-10C
-
8.85 × 10-10C
-
9.85 × 10-10C
-
-
13) The electric field in a region is given by
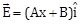 where E is in NC-1 and x in meters. The values of constants are A = 20 SI unit and B = 10 SI unit. If the potential at x = = 1 is V1 and that at x= -5 is V2 then V1 – V2 is:
where E is in NC-1 and x in meters. The values of constants are A = 20 SI unit and B = 10 SI unit. If the potential at x = = 1 is V1 and that at x= -5 is V2 then V1 – V2 is:-
320 V
-
-48 V
-
-520 V
-
180 V
-
-
14) A rectangle solid box of length 0.3 m is held horizontally, with one of its sided on the edge of a platform of height 5. When released, it slips off the table in a very short time = 0.01 s, remaining essentially horizontal. The angle by which it would rotate when it hits the ground will be (in radians) close to:
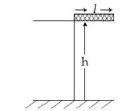
-
0.5 rad
-
0.6 rad
-
0.02 rad
-
0.28 rad
-
-
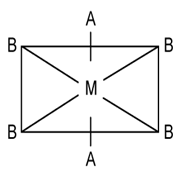
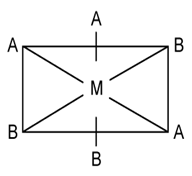
15) A uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut off, the coordinates of the centre of mass of the remaining portion will be:
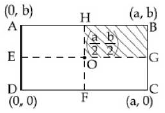
-
-
16) In the density measurement of a cube, the mass and edge length are measured as (10.00 ± 0.10) kg and (0.10 ± 0.01) m, respectively. The error in the measurement of density is:
-
8657.6 kg/m3
-
7248.3 kg/m3
-
6202.4kg/m3
-
6416.6 kg/m3
-
-
17) A signal A cos ?t is transmitted using ?0 sin ?0t as carrier wave. The correct amplitude modulated (AM) signal is:
-
V0 sin [?0 (1 + 0.01A sin ? t)t]
-
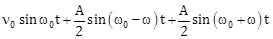
-
V0 sin ?0 t + A cos ? t)
-
(v0 + A) cos ? t sin ?0t
-
-
18) A body of mass 2 kg makes an elastic collision with a second body at rest and continues to move in the original direction but with one fourth of its original speed. What is the mass of the second body?
-
1.5 kg
-
1.2 kg
-
1.8 kg
-
1.0 kg
-
-
19) When heat Q is supplied to a diatomic gas of rigid molecules at constant volume its temperature increase by ?T. The heat required to produce the same change in temperature, at constant pressure is
-
-
20) Space between two concentric conducting spheres of radii a and b (b > a) is filled with a medium of resistivity ?. The resistance between the two spheres will be
-
-
21) Temperature difference of 120 °C is maintained between two ends of a uniform rod AB of length 2L. Another bent rod PQ, of same cross-section as AB and length
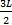 , is connected across AB (see figure). In steady state, temperature difference between P and Q will be closed to ________ °C.
, is connected across AB (see figure). In steady state, temperature difference between P and Q will be closed to ________ °C.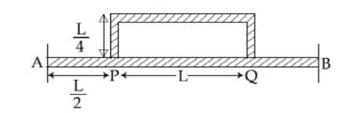
-
22) A gas can be taken from A to B via two different processes ACB and ADB. When path ACB is used 60 J of heat flows into the system. If path ADB is used work down by the system is 10 J. the heat flow into the system in path ADB is _____ J.
-
23) A copper wire is stretched to make it 0.5% longer. The percentage change in its electric resistance if its volume remains unchanged is ______.
-
24) A sample of radioactive material A, that has an activity of 10mCi (1 Ci = 3.7 × 1010 decays/s), has twice the number of nuclei as another sample of different radioactive material B which has an activity of 20mCi. The correct choice for half-lives of B is _______ days.
-
25) A conducting circular loop made of a thin wire, has area 3.5 × 10-3 m2 resistance 10 ?. It is placed perpendicular to a time dependent magnetic field B(t) = (0.4T) sin (50?t). The field is uniform in space. Then the net charge flowing through the loop during t = 0 s and t = 10 ms is close to ______ mC.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
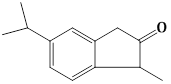
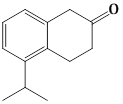
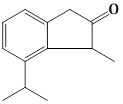
1) The major product of the following reaction is:
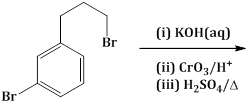
-
-
2) Arrange the following amine in the decreasing order of basicity:
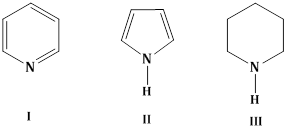
-
I > II > III
-
III > I > II
-
III > II > I
-
I > III > II
-
-
3) The compounds A and B in the following reaction are, respectively
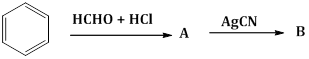
-
A = Benzyl alcohol, B = Benzyl cyanide
-
A = Benzyl chloride, B = Benzyl cyanide
-
A = Benzyl alcohol, B = Benzyl isocyanide
-
A = Benzyl chloride, B = Benzyl Isocyanide
-
-
4) Haemoglobin and gold sold are examples of:
-
positively and negatively charged sols, respectively
-
positively charged sols
-
negatively charged sols
-
negatively and positively charged sols, respectively
-
-
5) Sodium metal on dissolution in liquid ammonia gives a deep blue solution due to the formation of:
-
Sodium – ammonia complex
-
Sodamide
-
Sodium ion- ammonia complex
-
ammoniated electrons
-
-
6) Which of the following is NOT a correct method of the preparation of benzylamine from cyanobenzene?
-
(i) HCl/H2O (ii) NaBH4
-
(i) LiAIH4 (ii) H3O+
-
(i) SnCl2 + HCl(gas) (ii) NaBH4
-
H2/Ni
-
-
7) The correct statements among (a) to (b) regarding H2 as a fuel are:
- it produces less pollutants than petrol.
- A cylinder of compressed dihydrogen weight ∼30 times more than a petrol tank producing the same amount of energy.
- Dihydrogen is stored in tanks of metal alloys like NaNi5
- On combustion, values of energy released per gram of liquid dihydrogen and LPG are 50 and 142 kJ, respectively.
-
(b) and (d) only
-
(a) and (d) only
-
(b), (c) and (d) only
-
(a), (b) and (c) only
-
8) Consider the reaction
 The equilibrium constant of the above reaction is K3. If pure ammonia is left to dissociate, the partial pressure of ammonia at equilibrium is given by (Assume that PNH3 <<P total at equilibrium)
The equilibrium constant of the above reaction is K3. If pure ammonia is left to dissociate, the partial pressure of ammonia at equilibrium is given by (Assume that PNH3 <<P total at equilibrium) -
-
9) The correct order of the atomic radii of C, Cs, Al and S is:
-
C < S < Al < Cs
-
S < C < Cs < Al
-
S < C < Al, Cs
-
C < S < Cs < Al
-
-
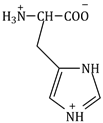
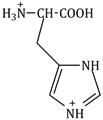
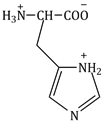
10) The correct structure of histidine in a strongly acidic solution (pH = 2) is:
-
-
11) Peptisation is a:
-
process of converting soluble particles to form colloidal solution
-
process of converting precipitate into colloidal solution
-
process of converting a colloidal solution into precipitate
-
process of bringing colloidal molecule into solution
-
-
12) The compound that is NOT a common component of photochemical smog is:
-
O3
-
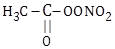
-
CH2=CHCHO
-
CF2Cl2
-
-
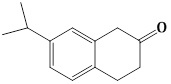
13) The major product of the following reaction is:
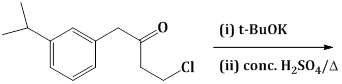
-
-
14) Which of the following compounds will show the maximum ‘enol’ content?
-
CH3COCH3
-
CH3COCH2CONH2
-
CH3COCH2COCH3
-
CH3COCH2COOC2H5
-
-
15) The correct statement about lCl5 and
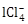 is:
is:-
lCl5 is trigonal bipyramidal and
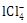 is tetrahedral
is tetrahedral -
lCl5 is square pyramidal and
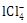 is square planer
is square planer -
lCl5 is square pyramidal and
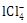 is tetrahedral
is tetrahedral -
Both are isostructual
-
-
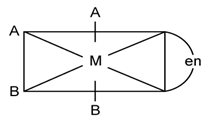
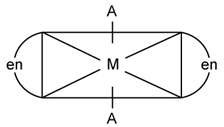
16) The one that will show optical activity is: (en = ethane -1, 2- diamine)
-
-
17) The major product of the following reaction is:
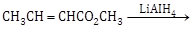
-
CH3CH2CH2CHO
-
CH3CH=CHCH2OH
-
CH3CH2CH2CO2CH3
-
CH3CH2CH2CH2OH
-
-
18) Which of the following statements is not true about sucrose?
-
The glycosidic linkage is present between C1 of ?-glucose and C1 of ?-fructose
-
It is a non-reducing sugar
-
It is also named as invert sugar
-
On hydrolysis it produces glucose and fructose
-
-
19) Air pollution that occurs in sunlight is:
-
oxidising smog
-
acid rain
-
reducing smog
-
fog
-
-
20) An example of a disproportion reaction is:
-
2KMnO4 ? K2MnO4 + MnO2 + O2
-
2NaBr + Cl2 ? 2naCl + Br2
-
2CuBr ? CuBr2 +Cu
-

-
-
21) In the reaction of oxalate with permanganate in acidic medium, the number of electrons involved in producing one molecule of CO2 is:
-
22) The volume strength of 1M H2O2 is: (Molar mass of H2O2 = 34 g mol–1)
-
23) 1 g of non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1: 5. The ratio of the elevation in their boiling points,
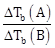 is
is -
24) An ideal gas is allowed to expand from 1 L to 10 L against a constant external pressure of 1 bar. The work done in kJ is:
-
25) An aqueous solution contains an unknown concentration of Ba2+. When 50 mL of a 1 M solution of Na2SO4 is added, BaSO4 just begins to precipitate. The final volume is 500 mL. The solubility product of BaSO4 is 1 × 10-10.
The original concentration of Ba2+ is ____×10-9 M
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) For x2 ? n? + 1, n ? N(the set of natural numbers), the integral

-
-
2) The plane through the intersection of the planes x + y + z = 1 and 2x + 3y – z + 4 = 0 and parallel to y-axis, also pass through the point:
-
(-3, 0,-1)
-
(-3, 1, 1)
-
(3, 3, -1)
-
(3, 2, 1)
-
-
3) Three circles of radii a, b, c (a < b < c) touch each other externally. If they have x – axis as a common tangent, then:
-
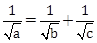
-
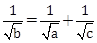
-
a, b, c are in A.P.
-
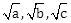 are in A.P.
are in A.P.
-
-
4) The tangent to the curve,
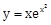 passing through the point (1, e) also passes through the point:
passing through the point (1, e) also passes through the point:-
(2, 3e)
-
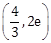
-
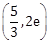
-
(3, 6e)
-
-
5) Two vertices of a triangle are (0, 2) and (4, 3). If its orthocenter is at the origin, then its third vertex lies in which quadrant?
-
third
-
second
-
first
-
fourth
-
-
6) The value of
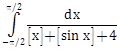 , where [t] denotes the greatest integer less than or equal to t, is:
, where [t] denotes the greatest integer less than or equal to t, is: -
-
7) Two circles with equal radii intersect at the points (0, 1) and (0, -1). The tangent at the point (0, 1) to one of the circles passes through the center of the other circle. Then the distance between the centres of these circles is:
-
1
-
2
-
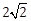
-
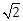
-
-
8) Let
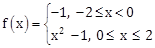 and g (x) = |f(x)| + f(|x|). Then in the interval (-2, 2), g is:
and g (x) = |f(x)| + f(|x|). Then in the interval (-2, 2), g is:-
differentiable at all points
-
not continuous
-
not differentiable at two points
-
not differentiable at one point
-
-
9) Let
 , where x and y are real numbers, then y – x equals:
, where x and y are real numbers, then y – x equals:-
91
-
-85
-
85
-
-91
-
-
10) 
-
-
11) If the function f given by f(x) = x3 - 3(a - 2)x2 + 3ax + 7, for some a ? R is increasing in (0, 1] and decreasing in [1, 5), then a root of the equation,
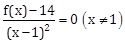 is:
is:-
-7
-
5
-
7
-
6
-
-
12) If the sum of the first 15 terms of the series
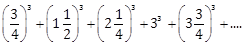 is equal to 225k, then k is equal to:
is equal to 225k, then k is equal to:-
108
-
27
-
54
-
9
-
-
13) If the system of linear equations
x - 2y + kz = 1
2x + y + z = 2
3x – y – kz = 3
Has a solution (x, y, z), z ? 0, then (x, y) lies on the straight line whose equation is:
-
3x – 4y – 1 = 0
-
4x – 3y – 4 = 0
-
4x – 3y – 1 = 0
-
3x – 4y – 4 = 0
-
-
14) In an ellipse, with centre at the origin, if the difference of the lengths of major axis and minor axis is 10 and one of the foci is at (0, 5
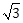 ), then the length of its latus rectum is:
), then the length of its latus rectum is:-
6
-
5
-
8
-
10
-
-
15) If three distinct numbers a, b, c are in G.P. and the equations ax2 + 2bx + c = 0 and dx2 + 2ex + f = 0 have a common root, then which one of the following statements is correct?
-
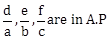
-
d, e, f are in A.P
-

-
d, e, f are in G.P
-
-
16) If the function f: R - {1, -1} ? A defined by
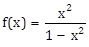 is surjective, then A is equal to:
is surjective, then A is equal to:-
R – [-1, 0)
-
R – (-1, 0)
-
R – {-1}
-
[0, ?)
-
-
17) If the line,
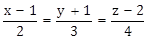 meets the plane, x + 2y + 3z = 15 at a point P, then the distance of P from the origin is:
meets the plane, x + 2y + 3z = 15 at a point P, then the distance of P from the origin is: -
-
18) The area (in sq. units) of the region A = {(x, y): x2 ? y ? x + 2} is:
-
-
19) The distance of the point having position vector
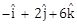 from the straight line passing through the point (2, 3, -4) and parallel to the vector
from the straight line passing through the point (2, 3, -4) and parallel to the vector 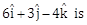
-
7
-
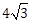
-
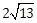
-
6
-
-
20) The integral
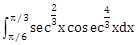 is equal to:
is equal to:-
35/6 – 32/3
-
35/3 – 31/3
-
37/6 – 35/6
-
34/3 – 31/3
-
-
21) Let a, b and c be in G.P. with common ratio r, where a ≠ 0 and 0 < r ≤
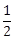 . If 3a, 7b and 15c are the first three terms of an A.P. such that the ratio of the 1st and the 4th terms is p : q. Then (p + q) is equal to __________.
. If 3a, 7b and 15c are the first three terms of an A.P. such that the ratio of the 1st and the 4th terms is p : q. Then (p + q) is equal to __________. -
22) Consider the differential equation,
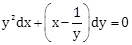 . If value of y is 1 when x = 1, then the value of x for which y = 1, is:
. If value of y is 1 when x = 1, then the value of x for which y = 1, is: -
23) For
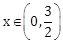 , let f(x) =
, let f(x) = 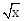 , g(x) = tan x and
, g(x) = tan x and 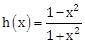 . If ? (x) = ((hof)og)(x) such that
. If ? (x) = ((hof)og)(x) such that  , then |p – q| is equal to:
, then |p – q| is equal to: -
24) Given that the truth value of the statement p → (∼q ? r) is false (F). If the truth values true (T) is represented as 1 and false (F) is represented as 0, then sum of the truth values of p, q and r is equal to ___________.
-
25) Let
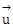 be a vector coplanar with the vectors
be a vector coplanar with the vectors 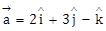 and
and 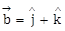 . If
. If 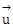 is perpendicular to
is perpendicular to  and
and  is equal to:
is equal to:
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25