Class 12-science H C VERMA Solutions Physics Chapter 12: Magnetic Field
Magnetic Field Exercise 230
Solution 1
![]()
![]()
![]() N towards west.
N towards west.
Solution 2
(a) By Right hand rule the electron will be deflected towards left.
(b) Kinetic energy, ![]()
![]() (horizontally)
(horizontally)
Magnetic force, ![]()
![]()
![]() (along west direction)
(along west direction)
Time taken to travel 1m in horizontal direction
![]()
![]()
In this time, deflection of electron in west direction
deflection![]()
deflection=![]()
deflection=![]()
deflection=![]()
deflection![]() m
m
deflection![]() cm
cm
deflection![]() cm
cm
Solution 3
Let
velocity of the particle in X-Y plane ![]()
Force on particle, ![]()
![]()
![]()
Comparing,
![]()
![]()
Velocity, ![]()
Solution 4
Since, force exerted by magnetic field is always perpendicular to each other.
So, ![]()
![]()
![]()
![]()
So, acceleration of particle is ![]() .
.
Solution 5
Time to travel 100m distance horizontally,
![]() sec
sec
Force on the bullet
![]()
![]()
![]()
Deflection due to the magnetic field![]()
deflection![]()
deflection=![]()
deflection![]() m
m
Solution 6
Magnetic field does not exert any force on a particle at rest.
So, initially force have been acted by electric field.
![]()
![]()
![]() (along west)
(along west)
When projected towards north, force will be exerted by both fields and in same direction as acceleration becomes thrice in same direction (along west).
![]()
![]()
![]()
![]()
![]() (into the paper perpendicularly)
(into the paper perpendicularly)
Solution 7
Force=i(l × B)
![]()
![]()
F ≈ 0.08N actin perpendicular to both wire and magnetic field.
Solution 8
The current will equally be divided at junction d.
So, current along dcb wire and dab wire is 1A.
Since, current, length and magnetic field for all wires is same then magnitude of force is equal.
Magnitude of force, ![]()
![]() N
N
Direction of force can be seen by Right hand rule.
On da and cb wire is towards left.
On dc and ab wire is downward.
Magnetic Field Exercise 231
Solution 9
Length of the wire in magnetic field=![]() m
m
Force of wire, ![]()
![]() N
N
Solution 10
![]()
![]()
![]()
![]()
Solution 11
Force, ![]()
![]()
![]() N upward in the
plane of paper.
N upward in the
plane of paper.
Solution 12
Magnetic field is radially outwards.
Magnetic field and length are perpendicular to each other.
Now, ![]()
![]()
![]()
Solution 13
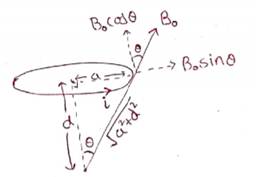
Magnetic force due to B0cosѲ field is radially outward which will be counter balanced by each other. So, force by B0cosѲ field is zero.
Magnetic force due to B0cosѲ field is in downward direction.
So, magnetic force F = Bill SinѲ
![]()
![]()
Solution 14
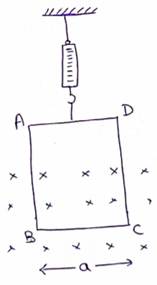
Initially, when current is flowing in anticlockwise direction the force on AB and CD wire are counter-balanced while force on BC is in upward direction.
![]()
![]()
![]()
So, initially Tension![]()
Later, when current is flowing in clockwise direction the force will act in downward direction of BC wire.
![]()
So, finally Tension![]()
Change in Tension![]()
Solution 15
Let the arbitrary loop be rectangle PQRS having length 'l' and breadth 'b'.
Magnetic field B is perpendicular to plane of loop.
Magnitude of force on QP and SR wire is![]()
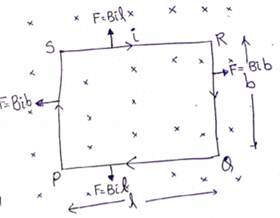
Both are in opposite direction. So will cancel each other.
Magnitude of force on PS and RQ wire is = Bib
Both are in opposite direction. So will cancel each other.
Therefore, net force acting on the loop is zero.
Solution 16
Let us consider a semi-circular wire of radius R is placed in uniform magnetic field directed perpendicular of wire.
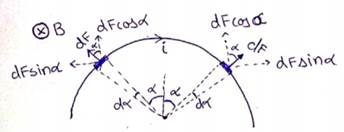
Considering two element at an angle ![]() as shown in figure.
as shown in figure.
Force acting on each element ![]()
Resultant force on both element ![]()
Resultant force![]()
![]()
![]()
![]()
![]() (distance between initial and final point)
(distance between initial and final point)
Solution 17
Length of wire![]()
Magnetic field, B=0.5T
Current, i=5A
Force![]()
![]()
F=0.25N
Solution 18
Magnetic force depends only upon distance between initial and final point not on shape of wire.
Length of wire![]()
Magnetic force, ![]()
![]()
![]()
Solution 19
Magnetic force depends only upon distance between initial and final point of wire.
Length of wire=2R
Force=![]()
![]()
F=2iRB
Solution 20
Under equilibrium
Magnetic force=Gravitational force
![]()
![]()
![]()
![]() T
T
Solution 21
(a) Switch 'S' is open
Weight of the rod is balanced by the tension in threads
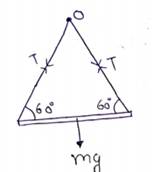
![]()
![]() N
N
(b) When switch is closed, magnetic force acts in downward direction given by right hand rule.
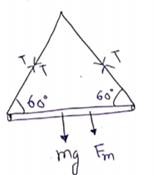
![]()
![]()
![]()
T=1.25N
Magnetic Field Exercise 232
Solution 22
When switch S is closed, current i flows in the wire. The magnetic force acts in rightward due to which rod moves with constant acceleration on rails. When separated from rails, it is retarded because of frictional force acting in opposite direction of motion.
Let it travels × distance before it stops.
Work done by magnetic force= work done by frictional force
![]()
![]()
Solution 23
When wire is about to slide
Frictional force= Magnetic force
![]()
![]()
![]()
![]()
![]()
Solution 24
When wire is about to slide
Frictional force=magnetic force
![]()
![]()
Solution 25
(a) Force on small segment of wire, ![]()
![]()
![]() towards center.
towards center.
(b) Let a small segment of wire subtends ![]() angle at the center of loop.
angle at the center of loop.
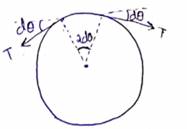
![]()
![]() angle is small]
angle is small]
![]()
Solution 26
In a magnetic field, the wire is in compressed state and when field is removed it will expand as no compression will be there.
We know that,
![]()
![]()
![]()
![]()
Solution 27
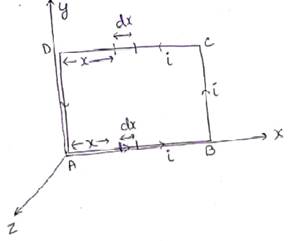
For wire AB and DC
Magnetic field at distance x is
![]()
Length of element=dx
Current in element=i
Since all parameters are same so magnitude of force is also same but opposite in direction. Hence force on wire AB and DC will cancel out each other.
For wire AB
Magnetic field=![]()
Length of wire=l
Current=i
force![]()
![]() (towards left)
(towards left)
For wire BC
Magnetic field![]()
Length of element=l
Current=i
![]()
![]() (toward right)
(toward right)
Net force on wire![]()
![]()
Solution 28
(a) Force on free electron of wire
![]()
![]()
(b) At equilibrium of electron
Electrostatic force=magnetic force
![]()
![]()
(c) Potential difference![]()
Solution 29
(a) ![]()
![]()
(b) Magnetic force, ![]()
![]()
![]()
![]()
(c) At equilibrium of electron
Electrostatic force = Magnetic force
![]()
![]()
![]()
(d) potential difference
![]()
![]()
Solution 30
Radius of circle, ![]()
![]()
![]()
Time period, ![]()
![]() sec
sec
Solution 31
Radius of the circle
![]()
![]()
![]()
![]()
![]() cm
cm
Solution 32
Relation between kinetic energy andradius of circle
![]()
![]()
![]() T
T
Number of revolutions per second, ![]()
![]() Hz
Hz
Solution 33
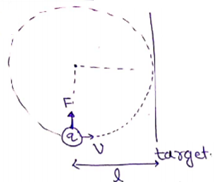
Proton just misses the target means
Radius<
![]()
![]()
![]()
![]()
Magnetic Field Exercise 233
Solution 34
Work done by potential difference
![]()
![]()
![]()
![]()
Now, radius of the circle
![]()
![]() cm
cm
Solution 35
(a) Force=![]()
![]()
![]() N
N
(b) Radius of the circle, ![]()
![]() m
m
(c) Time period![]()
![]() sec
sec
Solution 36
Force on the proton
![]()
![]()
![]()
![]()
Solution 37
(a)
![]()
![]() m/s
m/s
It is not reasonable as its speed is more than speed of light.
(b) For proton
![]() m/s
m/s
Solution 38
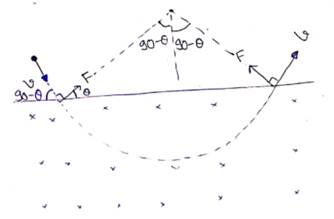
(a) Magnetic force = centripetal force
![]()
![]()
(b) Angle subtended at center of circle=![]()
(c) Time period ![]()
(d) If charge is negative.
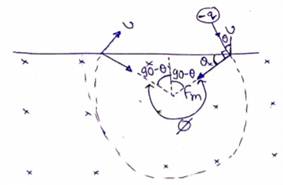
(i) Radius
Magnetic force = centripetal force
![]()
![]()
(ii) Angle subtended at center
![]()
![]()
(iii) Time period
![]()
Solution 39
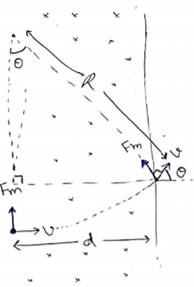
When width of the magnetic field is less than the radius of the circle of particle it will comes and if width of magnetic field is more than radius of circle of particle it will not come out.
![]()
(a) ![]()
![]()
![]()
(b) ![]()
![]()
![]()
(c) ![]()
It will not come out from forward direction but will describe a semicircle deviation = π
Solution 40
Distance between incident rays and emergent rays=2R
For first beam ![]() cm
cm
For second beam ![]() cm
cm
Radius of the circle is given by
![]()
![]()
![]()
![]()
![]()
Mass of 1st particle
![]()
![]()
![]() kg
kg
![]()
![]() amu
amu
So, ![]()
The two isotopes are of carbon ![]() .
.
Solution 41
Work done= charge![]() potential
difference
potential
difference
![]()
![]()
![]()
![]()
For isotopes with mass number 57
![]()
![]() m
m
![]() cm
cm
For isotopes with mass number 58
![]()
![]() m
m
![]() cm
cm
Solution 42
Kinetic energy, ![]()
For K-39
![]()
![]() m/s
m/s
Time to cross magnetic field
![]() sec
sec
Now acceleration in the magnetic field region
![]()
![]()
Displacement along y-direction in field
![]()
![]() m
m
Velocity in the vertical direction; ![]()
![]() m/s
m/s
Time to reach the screen=![]() sec
sec
During this time, distance travelled in vertical direction
=speed × time
![]() m
m
Net displacement from horizontal=![]()
![]() m
m
Similarly, for K-41
Net displacement from horizontal=![]() m
m
Net gap=![]() mm
mm
Solution 43
Radius of the circle for object
![]() cm
cm
Now, magnification
![]()
![]()
![]()
![]() cm negative sign shows that image is inverted.
cm negative sign shows that image is inverted.
Solution 44
Work done= charge × potential difference
![]()
![]()
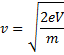
The electrons which are at slightly divergent angles will follow helical path.
Time period to complete one revolution of helical path
![]()
In this time period, distance travelled by electron along x-axis will be equal to pitch.
Pitch=![]()
Pitch=![]()
Magnetic Field Exercise 234
Solution 45
(a) for particles not to collide
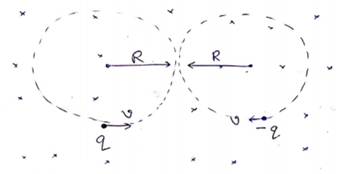
d>(R+R)
d>2R
![]()
![]()
Maximum speed of particles
![]()
(b)
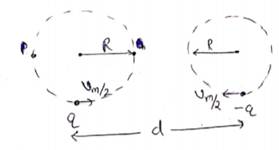
Radius of each circle=![]()
![]()
Minimum separation between particles=d-2R
=![]()
Maximum separation between particles=d+2R
![]()
(c) Radius od the particle will be
![]()
The particles will collide after
travelling ![]() distance in horizontal direction.
distance in horizontal direction.
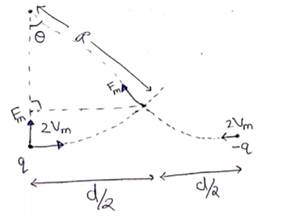
Angle rotated by the particle till collision occurs
![]()
![]()
![]()
Time taken=![]()
(d)
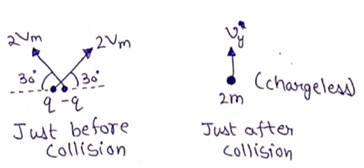
By momentum of conservation, ![]()
along x-axis,
![]()
![]()
along y-axis,
![]()
![]()
![]()
So, particle moves with constant speed along the straight line in upward direction after collision as it becomes chargeless.
Solution 46
Particle will move with constant velocity if
Magnetic force=gravitational force
![]()
![]()
![]() m/s
m/s
Solution 47
Radius of the circle=![]() cm
cm
![]()
If the particle moves with constant velocity
Electrostatic force= magnetic force
![]()
![]()
![]()
![]()
![]() C/Kg
C/Kg
Solution 48
Initially,
![]()
![]()
![]()
When electric field is switched off, the proton will move in a circle due to force by magnetic field.
![]()
![]()
magnetic field, B=0.05T
electric field, ![]() N/C
N/C
Solution 49
![]() C
C
![]() kg
kg
![]() m/s
m/s
![]() T
T
Component of velocity along magnetic
field=![]()
Component of velocity perpendicular to
magnetic field=![]()
Radius of the particle, ![]()
![]() m
m
Diameter=2R=2(0.18) =0.36m=36cm
Pitch=![]()
![]()
![]()
![]() cm
cm
Solution 50
m=![]() kg
kg
B=0.02T
R=5cm=![]() m
m
P=20cm=![]() m
m
Let
velocity of the particle perpendicular and parallel to magnetic field be ![]() respectively.
respectively.
Radius of helical path
![]()
![]()
![]() m/s
m/s
Pitch of helical path
![]()
![]()
![]() m/s
m/s
Solution 51
Let velocity of the particle after it travelled distance 'z' along z-axis.
![]()
Force on the particle
![]()
![]()
![]()
![]()
Since
particle is in y-z plane only, So ![]()
![]()
Force along z-axis
![]()
![]()
Also,
![]()
![]()
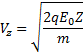
Solution 52
Electric field setup between the plates
of a capacitor, ![]()
Work done by electric field = change in kinetic energy
![]()
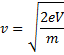
The electron will move in circular path
of radius, ![]()
Since electron doesn't strike upper plate
![]()
![]()
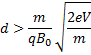
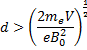
Solution 53
N=100 turns
![]()
I=2A
![]() N-m
N-m
We know that, ![]()
![]()
B=0.5T
Solution 54
(a) ![]()
![]()
![]() N-m
N-m
(b) Let angle between magnetic field
and plane of coil be ![]()
![]()
![]()
![]()
![]()
Solution 55
(a) Force acting on both longer sides is zero as angle between length of wire and magnetic field is zero.
Force on shorter sides are equal in magnitude but opposite in direction. Hence will cancel out each other.
So, net force on loop is zero.
(b) torque, ![]()
![]()
![]() N-m
N-m
Solution 56
![]()
N=500 turns
I=1A
![]()
Torque, ![]()
![]() N
N
Solution 57
(a) Length of wire=circumference of circle
![]()
![]()
Area of circular loop![]()
Torque, ![]()
![]()
![]()
(b) Length of the wire= perimeter of square of side 'a'
L=4a
![]()
Area of square=![]()
Torque, ![]()
![]()
![]()
Torque on circular loop is larger than square loop.
Solution 58
Torque by the magnetic field
![]()
![]()
![]()
For the coil to start tipping over
![]() torque due to gravitational
force
torque due to gravitational
force
![]()
![]()
Minimum magnetic field ![]()
Solution 59
(a) Current, ![]()
(b) magnetic moment, ![]()
![]()
(c) angular momentum
![]()
![]()
![]()
Putting this value in magnetic moment expression
![]()
Magnetic Field Exercise 235
Solution 60
Consider a ring at distance x from center and of width dx
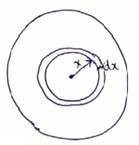
Charge on the elemental ring ![]()
![]()
Current due to rotation of this elemental ring
![]()
Magnetic moment due to elemental ring ![]()
![]()
Total magnetic moment![]()
![]()
![]()
![]()
Angular momentum
![]()
Divide (1) and (2)
![]()
![]()
Solution 61
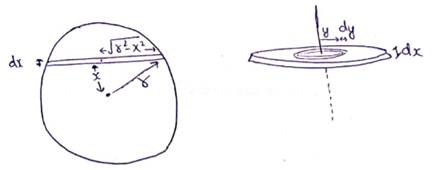
Consider a disc at distance x from center of sphere of thickness 'dx'
Consider an elemental ring at distance y of thickness 'dy' from center of disc
Charge on elemental ring![]()
![]()
Current due to elemental ring![]()
Magnetic moment due to elemental ring
![]()
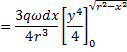
![]()
![]()
Magnetic moment for complete sphere
![]()
![]()
![]()
![]()
![]()
![]()
Angular momentum, ![]()
![]()
So, ![]()
![]()
