Class 12-science H C VERMA Solutions Physics Chapter 24 - The Nucleus
The Nucleus Exercise 442
Solution 1
We know,
![]()
![]()
Also,
![]()
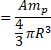


![]()
In CGS system,
Specific gravity=![]()
Solution 2
We know,
![]()
![]()
![]()
![]()
![]()
![]()
R=15km
Solution 3
![]()
And Binding energy = ![]()
Binding energy=28.2MeV
![]()
Solution 4
As given:
7![]()
Energy,
E=7Li![]()
![]()
=0.018076u
![]()
E=16.83MeV
Solution 5
Binding energy is:
![]()
![]()
![]()
For Au binding energy per nucleon
![]()
=7.73
Solution 6
(a) 238U→2He4+Th234
energy is:
E=[Mu-(NHe+ MTh)]u
=[238.0508-(234.04363+4.00260)]u
E=4.255MeV
(b) Energy is:
![]()
![]()
E=23.007MeV
Solution 7
223Ra→209Pb+14C
![]()
=223.018-(208.981+14.003)
=0.034
Energy is:
![]()
![]()
E=31.65MeV
Solution 8
Hydrogen contains only protons. Thus reaction will be:
![]()
![]()
∴ Minimum energy required is:
![]()
Solution 9
Energy released = (Initial mass of nucleus-Final mass of nucleus)C2
=(MZ.N-1+M0-MZN)C2
Solution 10
Energy is :
E=(31.974-31.972)u
![]()
=1.86MeV
Solution 11
(a) We know,
![]()
![]()
![]()
(b) Energy is:
E=[Mn-(MP+Me)]u
=[Mnu-Mpu-Meu]C2
=782159eV
=782.1keV
Solution 12
![]()
![]()
![]()
Solution 13
(a) EN=EP-K.E.
= 0.650-0.150=0.5MeV
= 500keV
(b) Momentum ![]()
![]()
Solution 14
![]()
![]()
![]()
(b) We know
Q=[Mass of reactants - mass of products]C2
Now for equation 1
Q=[39.9640u-39.9626u]C2
=1.3034MeV
For equation 2
Q=[39.9640u-39.9624u]C2
=0.4676MeV
For equation 3
Q=[39.9640u-39.9624u]uC2
=1.490MeV
Solution 15
![]()
![]()
![]()
Solution 16
Energy liberated =Mc-MB
=11.0114u-11.0093u
=933.6keV
Solution 17
Mass of 234Ra ![]()
=208563.0195MeV
![]()
![]()
=5.304MeV
Solution 18
According to question the reaction will be :
12N → 12C+e++v + v
Thus , energy is given as:
E(e++v)=E(N)-E(C12+v)
![]()
=12.89MeV
Solution 19
We know,
![]()
(a)
![]()
![]()
=64min
(b) Average life
![]()
=92min
c) ![]()
![]()
![]()
T=1598.23s
The Nucleus Exercise 443
Solution 20
(a) 198g of Au=Nr atoms
![]()
![]()
Activity =![]()
![]()
![]()
= 0.244curies
(b) We know,
![]()
![]()
= 0.040curies
Solution 21
(a) We know,
![]()
![]()
![]()
(b)
![]()
![]()
Solution 22
(a) ![]()
![]()
![]()
(b) Half-life of uranium, ![]()
![]()
![]()
(c) We know,
![]()
![]()
![]()
Solution 23
(a) We know,
![]()
![]()
![]()
(b) ![]()
![]()
![]()
![]()
Solution 24
![]()
![]()
![]()
![]()
Also,
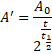
![]()
![]()
Solution 25
1 Mole of RaCl2=226+71=297g
Now
![]()
![]()
![]()
![]()
And activity=![]()
![]()
![]()
Solution 26
After 9 hours
![]()
![]()
=0.536Ci
Now, no. of atoms after 9th hour
![]()
![]()
![]()
Activity after 10 hours
![]()
![]()
=0.5Ci
Atoms left after 10th hour
![]()
![]()
![]()
![]()
![]()
Total no. of disintegration in tenth hour is :
![]()
![]()
![]()
Solution 27
We know,
![]()
![]()
=186.9
![]()
Solution 28
![]()
![]()
![]()
Emission rate is reduced to half
from ![]() ∴ the
amount of emission of cobalt should be reduced to half.
∴ the
amount of emission of cobalt should be reduced to half.
Thus, the required time is 270days.
Solution 29
(a) ![]()
Thus, it is 𝛽+ decay.
(b) Initially for carbon 90 N0 and boron 10 N0 and finally for carbon 10 N0 and boron 90 N0.
![]()
![]()
Solving we get
t=64.3
![]()
Solution 30
(a) We know,
Activity ![]()
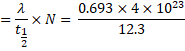
![]()
(b) Number of decays in 10 hrs is:
![]()
![]()
(c) We know,
![]()
![]()
![]()
Now,
No. of atoms disintegrated is:
![]()
![]()
![]()
Solution 31
Total counts radiated = counts received per cm2× Total area
![]()
![]()
Also,
![]()
![]()
![]()
![]()
Solution 32
Initially,
Total no. of uranium atoms= No. of atoms of U + No. of atoms of Pb
![]()
![]()
Also
![]()
![]()
![]()
Solution 33
We know,
![]()
After 't' time is passed,
![]()
![]()
![]()
Solution 34
According to question :
Activity of bottle on mountain = 1.5% × Activity of bottle 8 years before
![]()
![]()
![]()
t= 83.75 years
Solution 35
(a) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
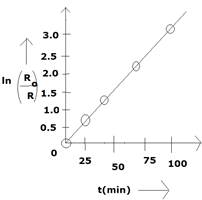
b) From graph,
![]()
c) Half-life,![]()
![]()
Solution 36
We know,
A=dN
![]()
![]()
Now if
![]()
![]()
And ![]()
![]()
Also, abundance in potassium ![]()
Solution 37
(a) Here,
![]()
Neutrino is emitted is the decay.
(b) We know,
![]()
![]()

Solving we get,
![]()
![]()
Solution 38
Rate of radioactive decay is given as:
![]()
According to the question, after some time the number of active nuclei will become constant. Thus,
![]()
![]()
Also,
![]()
![]()
![]()
Solution 39
Number of radioactive particles present at 't' time is given as:
![]()
And particles that decay are given as:
![]()
![]()
![]()
Solution 40
We know,
![]()
![]()
![]()
Also
![]()
![]()
Now,
Fraction of activity ![]()
![]()
![]()
Solution 41
No. of atoms is:
![]()
![]()
Activity ![]()
![]()
Or 729Ci
The Nucleus Exercise 444
Solution 42
(a) ![]()
![]()
b) At t=/hr
Bi will be decayed to half as ![]()
![]()
Now,
Mass of ![]()
![]()
=0.175g
Similarly for ![]()
Mass of ![]()
=0.325g
Solution 43
(a) We know, ![]() disintegration/s
disintegration/s
Now we will find ![]() for all values.
for all values.
![]()
![]()
![]()
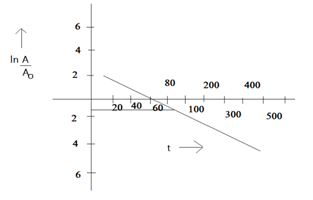
![]()
![]()
![]()
![]()
![]()
![]()
(b) ![]() for 100 Ag = 24.4s
for 100 Ag = 24.4s
(c) ![]()
=0.0284
And also,
![]()
![]()
![]()
(d)
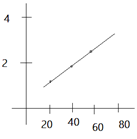
(e)According to above graph ![]() 108Ag)
108Ag)
Solution 44
We know,
![]()
= 4.8h
Also ![]()
![]()
![]()
Solution 45
We know
![]()
![]()
![]()
Solution 46
After 't' time
![]()
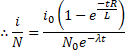
![]()
![]()
![]()
Solution 47
1g of I =0.007g U235
![]()
![]()
And
1 atom=200MeV
![]()
![]()
Solution 48
Power = Total energy emitted per seem
![]()
![]()
![]()
And we know that
![]()
![]()
=3.7mg
Solution 49
(a) No. of fission per second=![]()
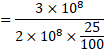
![]()
(b) ![]()
and so ![]()
=1.26kg/day
Solution 50
(a) Q value ![]()
![]()
=4.05MeV
(b) Q value ![]()
![]()
=3.25MeV
(c) Q value ![]()
![]()
=17.57MeV
Solution 51
We know,
![]()
And ![]()
![]()
![]()
Solution 52
Q value = ![]()
![]()
=-93.1KeV
Solution 53
![]()
![]()
![]()
% of deuterium
![]()
Energy of deuterium ![]()
=[2![]() (2H)-m(3H)-mp]C2
(2H)-m(3H)-mp]C2
=[2![]() 2.014102-3.016049-1.007276]uC2
2.014102-3.016049-1.007276]uC2
=4.54MeV or 7.262![]()
![]()

