Class 12-science H C VERMA Solutions Physics Chapter 20 - Photoelectric Effect and Wave-Particle Duality
Photoelectric Effect and Wave-Particle Duality Exercise 365
Solution 1
Given data:-
λ1 = 400 nm
λ2 = 780 nm
We know,
h = 6.63×10-34Js
c = 3×108 m/s
Energy of photon is given by,
E=hv
ν=c / λ
∴ E =hc / λ
Energy E1 of a photon of wavelength λ1
E1=hc / λ1
=6.63×10-34 ×3×108 / 400×10-9
=5×10-19 J
Energy E2 of a photon of wavelength λ2
E2 =6.63×10-34 ×3×108 / 780×10-9
=2.55×10-19 J
Thus, The range of energy is between 2.55 × 10-19 J and 5 × 10-19 J.
Solution 2
Given data:
λ= 500 nm
h = 6.63×10-34 Js
Momentum of a photon of light is,
p=h /λ
=6.63×10-34 / 500×10-9
=1.33×10-27 kg-m/s
Solution 3
Given data:
λ1= 500 nm
λ2= 700 nm
c = 3×108 m/s
h = 6.63×10-34 Js
Energy of absorbed photon is-
E1=hc /λ1
=hc / 500×10-9
Energy of emitted photon,
E2=hc /λ2
=hc / 700×10-9
Energy absorbed by the atom in the process:
E1 - E2 = hc(1 /λ1 - 1/ λ2)
=6.63×3×10-19(1/5 - 1/7)
=1.136×10-19 J
Solution 4
Given data:
P = 10 W
λ = 590 nm
Energy consumed per second = 10 J
Energy converted into light = 60 %
∴ Energy converted into light = 60 / 100 ×10 =6 J
Energy needed to emit one photon from the sodium is:
E =hc /λ
=6.63×10-34 ×3×108 / 590×10-9
=19.89/590 10-17 J
Number of photons emitted are:
N = 6 / E
=6 / (19.89/590 10-17)
N = 1.77 × 1019
Solution 5
Given Data:
Intensity of light is I = 1.4 × 103 W/m2
λ = 500 nm
d= 1.5×1011 m
Intensity is given as:
I=Power/ Area
=1.4×103 W/m2
Let n be the number of photons emitted per second.
∴ P=nhc / λ,
Number of photons/m2 = nhc / λ×A
=nhcλ×1 = I
∴ n=I×λ / hc
=1.4×103 ×500×10-9 / 6.63×10-34 ×3×108
=3.5×1021
(b) Consider number of two parts at a distance r and r + dr from the source.
Let dt be the small time interval
Total number of photons emitted in this time interval,
N=ndt
= (P λ / hc × A) dr / c
These points will be between two spherical shells of radius r and r + dr. It will be the distance of the 1st point from the sources.
No. of photons/m3
=P λ / 4πr2hc2
=1.4×103×500×10-9 / 6.63×10-34 ×9×1016
=1.2×1013
(c) Number of photons emitted = (Number of photons / s-m2)× Area
=(3.5×1021) ×4⊓l2
=3.5×1021×4× (3.14) × (1.5×1011)2
=9.9×1044
Solution 6
Given Data:
λ=663×10-9 m
θ=60°
Number of photons per second, n=1×1019
Momentum of photon is
p=h /λ
Force exerted on the wall is
F=n× (pcosθ- (-pcosθ))
=2npcosθ
=2×1×1019 ×10-27 ×0.5
=1.0×10-8 N
Force exerted by the light beam on the mirror is 1.0×10-8 N
Solution 7
Given Data:
P = 10 watt
We know that,
λ=h / p
⇒ p=h / λ
On dividing both sides by t,
we get:
p / t=h / λ t ….....(1)
Energy is given as
E=hc / λ
⇒ E / t=hc / λ t
Let P be the power. Then,
P=E / t
=hc / λ t
P =pc / t
⇒ P/c =p/t
F=p/t
=P/c
F = 7/10(absorbed) + 2×3/10(reflected)
F=7/10× P/c + 2×3/10 × P/c
F = 4.33×10-8 N
Solution 8
Given that:
m = 20 g = 20 × 10-3 kg
The weight of the mirror will be balanced if the force exerted by the photons will be equal to the weight of the mirror.
Now,
p=h / λ
On dividing both sides by t,
P/t=h/ λ t .....(1)
E = hc / λ
⇒ E/t = hc/ λ t
P be the power. Then,
P=Et=hc / λ t
P=pc/t
⇒ P/c = p/t
F=P/t = P/c
Thus, rate of change of momentum = Power/c
As the light gets reflected normally,
Force exerted = 2×(Rate of change of momentum) = 2 × Power/c
30%of (2×Power/c)=mg
⇒ Power = 20×10-3 ×10×3×108 ×10 /2×3
=100 MW
Solution 9
Given that,
P= 100 W
R = 20 cm = 0.2 m
It is given that 60% of the energy supplied to the bulb is converted to light.
Therefore, power of light emitted by the bulb, P = 60 W
F=P/c
F=60 / 3×108
=2×10-7 N
Pressure = Force / Area
=2×10-7 / 4×3.14× (0.2)2
=4×10-7 N/m2
Solution 10
Given that,
r = 1 cm
I = 0.5 Wcm-2
Let A be the effective area of the sphere perpendicular to the light beam.
So, force exerted by the light beam on sphere is given by,
F=P/c=AI/c
F = ⊓× (1)2 ×0.5 / 3×108
=5.2×10-9 N
Solution 11
Consider az sphere of centre O and radius OP. As shown in the figure, the radius OP of the sphere is making an angle θ with OZ. Let us rotate the radius about OZ to get another circle on the sphere. The part of the sphere between the circle is a ring of area 2⊓r2sinθdθ.
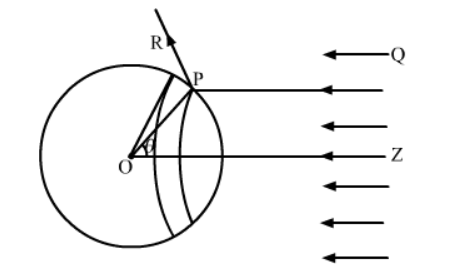
Consider a small part of area ΔA of the ring at point P.
Energy of the light falling on this part in time Δt,
ΔU=IΔt(ΔAcosθ)
As the light is reflected by the sphere along PR, the change in momentum,
Δp=2![]() cosθ
cosθ
=![]() IΔt(ΔAcos2θ)
IΔt(ΔAcos2θ)
Therefore, the force will be
![]() =
= ![]() IΔAcos2θ
IΔAcos2θ
The component of force on ΔA, along ZO, is given by
![]() cosθ =
cosθ = ![]() IΔAcos3θ
IΔAcos3θ
Now, force action on the ring,
dF=![]() I(2πr2sinθdθ) cos3θ
I(2πr2sinθdθ) cos3θ
The force on the entire sphere is given by integral of
F=![]()
=(πr2I/c)
Solution 12
We can apply the principle of conservation of energy to this collision of electron with a photon.
So, using principle of conservation of energy:
pc + mec2 =√( p2 c2 + me2c4) …………(1)
Where,
me = rest mass of electron
pc = energy of the photon
Squaring on both side of equation (i),
(pc + mec2)2 = ( p2 c2 + me2c4)
⇒pc + mec2 +2pc×mec2 = (p2 c2 + me2c4)
⇒2pc×mec2 = 0 or pc=0 …..(since, me andc are non-zero)
This is giving null energy of photon which is not possible.
Solution 13
Given Data:-
r = 1 m
Electric potential energy is given by
E1= kq2r = kq2,
where k is 1/4⊓ɛ0
Energy of photon is given by
E2 = hc / λ,
Given that, E1 = E2
∴ kq2 =hc / λ
⇒ λ =hc / kq2
For λ to be maximum q should be minimum.
q = e =1.6×10-19 C
λ = hc / kq2
= 6.63×3×10-34 ×108 / 9×102 × (1.6)2×10-38
= 863 m
Next smaller wave length,
λ =6.63×3×10-34 ×108 / 9×102 ×4× (1.6)2×10-38
=215.74 m
Solution 14
Given Data :-
λ = 350 nm
ϕ = 1.9 eV
From Einstein's photoelectric equation,
E= φ + Kinetic energy of electron
⇒K.E. =E - φ
Maximum kinetic energy of electrons,
Emax =hc/λ - ϕEmax =6.63×10-34×3×108 / 350×10-9×1.6×10-19 - 1.9Emax
Emax =1.6 eV
Solution 15
Given Data:-
W0 = 2.5 × 10-19 J
v = 6.0 × 1014 Hz
(a) Work function of a metal,
W0 = hv0,
∴ v0 = W0/h
⇒ v0 = 2.5×10-19 / 6.63×10-34
=3.8×1014 Hz
(b) Einstein's photoelectric equation gives
ev0 =hv - W0,
∴ v0=(hv - W0)/e
= (6.63×10-34×6×1014 - 2.5×10-19) / 1.6×10-19
=0.91 V
Solution 16
Given Data:
φ = 4 eV = 4×1.6×10-19 J
V0 = 2.5 V
(a) Work function of a photoelectric material,
φ = hc/λ0
∴ λ 0 = hc/φ
λ 0=6.63×10-34 ×3×108 / 4×1.6×10-19
λ 0 = 3.1×10-7 m
(b) From Einstein's photoelectric equation,
E=φ+eV0
On substituting the respective values,
hc / λ = 4×1.6×10-19 +1.6×10-19×2.5
⇒ λ =1.9125×10-7
Solution 17
Given Data:-
λ = 400 nm
φ = 2.5 eV
Using Einstein's photoelectric equation,
Kinetic energy=hc/ λ - φ
∴K.E.=(6.63×10-34 ×3×108 /4×10-7 ×1.6×10-19) - 2.5 eV
=0.605 eV
And K.E. =p2/2m,
∴p2=2m×K.E.
⇒ p2=2×9.1×10-31×0.605×1.6×10-19
⇒p=4.197×10-25 kg-m/s
Solution 18
Given Data:
λ = 400 nm
V0 = 1.1 V
Using Einstein's photoelectric equation,
hc/ λ =hc / λ 0 + eV0,
Here, λ 0 = threshold wavelength
V0 = stopping potential
On substituting the respective values in the above formula, we get:
6.63×10-34 ×3×108 /400×10-9 = (6.63×10-34 ×3×108 / λ0) +1.6×10-19 ×1.1
λ0 =6.196×10-7 m
Threshold wavelength for the metal is 6.196×10-7 m
Solution 19
(a)
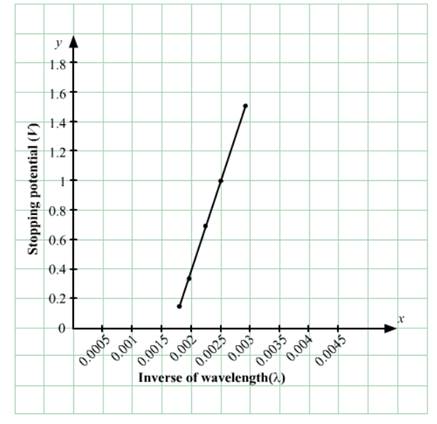
When λ = 350, Vs = 1.45
and when λ = 400, Vs = 1
∴ hc/350=w +1.45 ...(1)
And hc /400= w +1 .....(2)
Subtracting (2) from (1), we get:
h = 4.2 × 10-15 eVs
(b) Now, work function,
w= (12240 / 350) -1.45
=2.15ev
(c) w= nc/ λ
λthreshold = hc/w
λthreshold =576.8 nm
Solution 20
Given Data:-
E = 1.2 × 1015 times per second
v = 1.2×1015 / 2
=0.6×1015 Hz
φ = 2.0 eV
Using Einstein's photoelectric equation,
K=hv - φ0
⇒ K=6.63×10-34 ×0.6×1015 /1.6×10-19 - 2
=0.486 eV
Solution 21
Given Data:
E= E0sin[(1.57×107 m-1 )(x-ct)]
φ = 1.9 eV
Comparing the given equation with the standard equation,
E= E0sin(kx-wt), we get:
ω=1.57×107 ×c
For frequency,
v=1.57×107 ×3×108 / 2⊓ Hz
Using Einstein's photoelectric equation,
e V0 =hv - φ
Substituting the values, we get
e V0 =6.63×10-34 ×(1.57×3×1015 / 2π) ×1.6×10-19 - 1.9eV
⇒ V0=1.205×1.6×10-19/ 1.6×10-19
=1.205 V
The value of the stopping potential is 1.205 V.
Photoelectric Effect and Wave-Particle Duality Exercise 366
Solution 22
Given Data:
E=(100 Vm-1)sin [(3.0×1015 s-1)t ] sin [(6.0 ×1015 s-1)t]
=100×12cos [(9×1015 s-1)t]-cos[(3×1015 s-1)t]
Angular frequency ω are 9 × 1015 and 3 × 1015 .
φ = 2 eV
Maximum frequency,
v=ωmax /2π = 9×1015 / 2π Hz
Using Einstein's photoelectric equation,
K = hv - φ
⇒K = 6.63×10-34 × (9×1015 / 2⊓) × (1/1.6×10-19 ) - 2 eV
⇒K = 3.938 eV
Solution 23
Given Data:
Intensity I = 5 mW
Number of photons emitted per second are n = 8 × 1015
V0 = 2 V
E = hv = I/n = 5×10-3 / 8×1015
Using Einstein's photoelectric equation
W0 = hv - eV0
Substituting the values, we get:
W0 =5×10-3/8×1015 - 1.6×10-19 ×2
=3.05×10-19 J
=1.906 eV
Solution 24
We have to take two cases.Case(I) :- When stopping potential,
V0=1.656 volts
v=5×1014 Hz
Case(II):- When stopping potential,
V0=0
v=1×1014 Hz
Using Einstein's equation,
eV0=hv - W0
Using the values of above two cases,
we get:
1.656e = 5h×1014 - W0 …....(1)
0 = 5h×1014 - 5×W0 …...(2)
Subtracting equation(2) from (1), we get:
W0= 1.656 eV / 4
=0.414 eV
Using the value of W0 in equation (2), we get:
⇒ 5W0 = 5h×1014
h/e= 4.414×10-15 Vs
Solution 25
Given Data:-
W0 = 0.6 eV
Now, work function,
W0 = hcλ,
∴λ=hc / W0
=6.63×10-34 ×3×108 / 0.6×1.6×10-19
=2071 nm
The maximum wavelength of light that can be recorded by the film is 2071 nm.
Solution 26
Given Data:-
λ = 400 nm
P = 5 W
E = hc/ λ
=(1242 / 400) eV
and no. of photons = P/E
=5×400 / 1.6×10-19×1242
Number of electrons = 1 electron per 106 photons
Number of photoelectrons emitted are:
n' = 5×400 / 1.6×1242×10-19 ×106
I = n' × Charge on electron
I = ( 5×400 / 1.6×1242×10-19×106 ) ×1.6×10-19
=1.6 μA
Solution 27
Given Data:-
r = 4.8 cm
λ = 200 nm
E = 1.0 × 10-7 J
According to condition one photon out of every ten thousand is able to eject a photoelectron.
Energy of one photon,
E'=hc / λ
E' =6.63×10-34×3×108 / 2×10-7
=9.945×10-19
Number of photons,
n = E / E
= 1×10-7 / 9.945×10-19
= 1×1011
Number of photoelectrons = 1×1011 / 104= 1×107
The amount of positive charge developed due to the outgoing electrons is given by,
q = Number of photoelectrons × charge on a electron
=1×107×1.6×10-19 =1.6×10-12 C
Potential developed at the centre as well as on surface,
V=Kq / r, ……(K = 14⊓ε0)
∴ V = 9×109×1.6×10-12 / 4.8×10-2
=0.3 V
So, 0.3 V is potential at the centre of the sphere.
Solution 28
Given Data:-
d = 10 cm
φ = 2.39 eV
λ1 = 400 nm
λ2 = 600 nm
We know that, Magnetic field B will be minimum if energy is maximum.
And for maximum energy, wavelength λ should be minimum.
Using Einstein's photoelectric equation:
E = hc / λ - φ
∴ E=1242 / 400 - 2.39
=0.715 eV
We know that, the beam of ejected electrons will gwt bent by the magnetic field. There will be no current, if the electrons do not reach the other plates.
When a charged particle is sent perpendicular to a magnetic field, it moves along a circle of radius,
r = mv / qB,
We wanted that no current flows in the circuit. So, radius of the circle should be equal to r = d,
Using mv = √(2mE)
⇒ r=√![]() )
)
⇒0.1=√(2×9.1×10-31×1.6×10-19×0.715 / 1.6×10-19×B)
⇒B=2.85×10-5 T
Solution 29
Given Data:-
y = 1 mm × 2 = 2 mm
W0 = 2.2 eV
D = 1.2 m
d = 0.24 mm
y=λD / d
∴ λ=2×10-3×0.24×10-3 / 1.2
= 4×10-7 m
E=hc / λ
= 4.14×10-15×3×108 / 4×10-7
= 3.105 eV
Using Einstein's photoelectric equation, we have,
eV0=E - W0
∴ eV0 = 3.105 - 2.2=0.905 eV
V0=0.905 / 1.6×10-19×1.6×10-19 V
= 0.905 V
The stopping potential V needed to stop the photocurrent is 0.905 V.
Solution 30
Given Data:-
φ= 4.5 eV,
λ = 200 nm
Using Einstein's photoelectric equation, we have,
K = E - φ
= hc /λ - φ
∴ K=1242 / 200 - 4.5
= 1.71 eV
At least 1.7 eV is required to stop the electron and thus minimum kinetic energy is 2 eV.
According to given condition that electric potential of 2 V is required to accelerate the electron. Therefore, maximum kinetic energy
= (2+1.7) eV
= 3.7 eV
Solution 31
Given Data:-
σ = 1.0 × 10-9 Cm-2
φ = 1.9 eV
λ= 400 nm
d = 20 cm
V = E × d,
∴ V=σ/ε0×d
=1×10-9×20 / 8.85×10-12×100
=22.598 V=22.6 V
Using Einstein's photoelectric equation, we have:
eVo=hv - W0
=hc /λ - W
V0=4.14×10-15×3×108 /4×10-7 - 1.9
=1.205 V
As V0 is much less than 'V', the minimum energy required to reach the charged plate must be equal to 22.7eV.
For maximum KE, 'V' must have an accelerating value.
Hence maximum kinetic energy,
K.E.=V0+V
=1.205+22.6
=23.8005 eV
Solution 32
We know that,
E = σ / ε0
=1×10-9 / 8.85×10-12
=113 V/m
Acceleration is given by
a=![]()
a = 1.6×10-19×113 / 9.1×10-31
=19.87×1012
T = √(2y/a)
=√(2×20×10-2 / 19.87×1012)
=1.41×10-7 s
In previous problem we got KE = 1.2eV
Using Einstein's photoelectric equation, we have,
K.E.=hc /√ - W
=1.2 eV=1.2×1.6×10-19 J
∴Velocity is v=√![]() )
)
=√(2×1.2×1.6×10-19 / 4.1×10-31)
=0.665×10-6 m/s
∴ Horizontal displacement,
S = v×t
=0.665×10-6 ×1.4×10-7
=0.092 m
Solution 33
Given Data:-
φ = 1.9 eV
λ = 250 nm
Energy of a photon,
E=hc / λ
∴E =![]() = 4.96 eV
= 4.96 eV
Using Einstein's photoelectric equation, we have,
K=E - φ
⇒ K= hc /λ - φ
=4.96 eV - 1.9 eV
=3.06 eV.
For non-positive velocity of each photo electron, the velocity of a photoelectron should be equal to minimum velocity of the plate.∴ Velocity is given by,
v=√(2K/m)
∴ v= √(2×3.06×1.6×10-19 / 9.1×10-31)
=1.04×106 ms-1
Solution 34
Using Einstein's photoelectric equation,
eV0=hc /λ - φ
⇒V0=(hc / λ - φ)(1/e)
The particle will move in a circle when the stopping potential is equal to the potential due to the singly charged ion at that point so that the particle gets the required centripetal force for its circular motion.
⇒Ke / 2d=(hc / λ - φ)(1/e)
⇒hc / λ =Ke2 /2d + φ = (Ke2+2dφ) /2d
⇒ λ =(hc)(2d) /(ke2+2dφ)
⇒ λ = 8⊓∊0hcd /(e2+8⊓∊0dφ)
Solution 35
Given Data:-
λ= 400 nm
ϕ = 2.2 eV
E=hc / λ
∴E=![]() = 3.1 eV
= 3.1 eV
This energy will be supplied to the electrons.
Energy lost is
= 3.1 eV × 10%
= 0.31 eV
Now, energy of the electron after the first collision = 3.1 - 0.31 = 2.79 eV
Energy lost in the second collision
= 2.79 eV× 10%
= 0.279 eV
Total energy lost in two collisions
= 0.31 + 0.279 = 0.589 eV
Using Einstein's photoelectric equation,
K = E - φ - energy lost in collisions
= (3.1 - 2.2 - 0.589) eV
= 0.31 eV
(b) Similarly for the third collision,
The energy lost = (2.79 - 0.279) eV × 10%
= 0.2511 eV
Energy after the third collision = 2.790 - 0.2511 = 2.5389
Energy lost in the fourth collision = 2.5389 × 10%
Energy after the fourth collision = 2.5389 - 0.25389 = 2.28501
After the fifth collision, the energy of the electron becomes less than the work function of the metal.
Therefore, the electron can suffer maximum four collisions before it becomes unable to come out of the metal.

