Class 12-science H C VERMA Solutions Physics Chapter 2 - Kinetic Theory of Gases
Kinetic Theory of Gases Exercise 34
Solution 1
Pa
n=1 mol
T=273 K
R=8.3 J/mol-K
PV=nRT
Solution 2
Pa; 
; T=273 K; R=8.3 J/mol-K
PV=nRT
PV=
N=
=
Solution 3
Pa
T=273 K
Solution 4
At STP, 22.4 ltr. of oxygen contains 32gm of oxygen.
gm
mg
Solution 5
Since mass is same,
Ideal gas equation
PV=nRT
Solution 6
PV=nRT
Solution 7
Ideal gas equation:
PV=nRT
P
T
375 K
Solution 8
mol
PV=nRT
Pa
Solution 9
Solution 10
0.987
Solution 11
Initially,
So, 
Now,
(diathermic separator)
Since, 
Solution 12
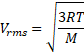
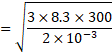
m/s
m/s
Now,
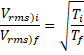
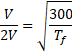
1200 K
Solution 13
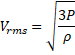
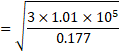
=1300 m/s
Solution 14
310K
Solution 15
445.25 m/s
We know,
[R=6400 km]
sec
Solution 16
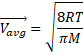
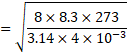
1201.35 m/s
Momentum=m
=
=
Kg-m/s
Solution 17
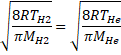
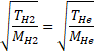
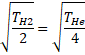
Solution 18
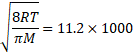
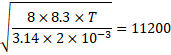
11800 K
Kinetic Theory of Gases Exercise 35
Solution 19
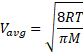
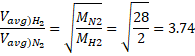
Solution 20
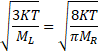
1.18
Solution 21
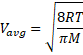
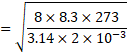
=1687 m/s
Time between two
collisions=
sec
Number of collision in 1
sec=
Solution 22
(a)
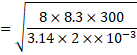
=1781 m/s
1780 m/s
(b)
Change in momentum of
molecule=mv
(mv)
=
mv
Total DP
for N molecules=
Mass of a molecule
Kg
So, 
Solution 23
PV=nRT
Solution 24
Initially,
Now
Mass of gas leaked=
= 1.446-1.285
= 0.16 gm
Solution 25
Since temperature and number of moles are constant.
Solution 26
Initially,
atm; 
Now,
No. of moles leaked=
=0.16-0.02
=0.14
Solution 27
T-100=96.38
T=196.38
T≈196
Solution 28
=constant
=constant
TV=constant
Solution 29
2250 Pa
Solution 30
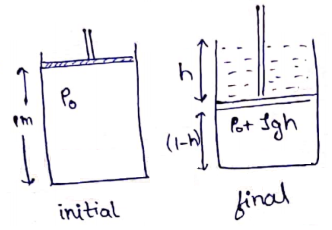
No of moles initially=No of moles finally [∵ Container is closed]
h=0.25 m
h=25 cm
Solution 31
No. of moles initially= No. of moles finally
Solution 32
(a) 
(b) 
(c) 
P≈73.16 kPa
P≈73 kPa
Solution 33
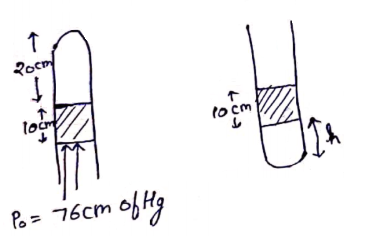
No. of moles initially=No. of moles finally
h=15.3 cm
h≈15 cm
Solution 34
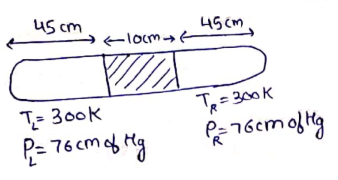
No of moles in left side=No of moles in Right side
[∵Initially P,V,R,Tis same on both sides.]
Now,
400l=273(90-l)
673l=273×90
l=36.5 cm
Solution 35
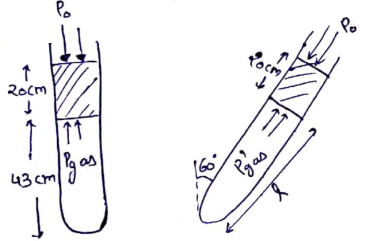
cm of Hg
cm of Hg
cm of Hg
cm of Hg
No. of moles initially=No. of moles finally
l=48 cm
Kinetic Theory of Gases Exercise 36
Solution 36
Initially,
By ideal gas equation
divide
- (i)
Now,
By ideal gas equation,
divide
(ii)
From (i) and (ii)
from left end.
Solution 37
Let at any time t, pressure and no. of moles be P and n respectively.
So, 
In dt time, dn moles are taken out and pressure decreases by dP.
-(i)
The pressure of gas taken out is equal to the inner pressure.
-(ii) [Here dP.dV0]
From (i) and (ii)
(b) When half gas is leaked out, pressure will become half of initial.
So, 
Taking in on both the sides.
Solution 38
[Using PV=nRT]
Now, 
[Here n=1]
Solution 39
Internal energy=
Since pressure P is constant and V=Volume of room is also constant.
So, U=Constant.
Solution 40
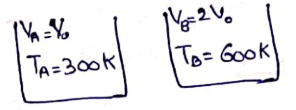
No. of moles at 300 K=No. of moles at 600 K(just before cork comes out)
Pascal
Net force on cork by gas
and atmosphere at 600 K=
Newton
Just before cork comes out
Now,
Solution 41
(a) The pressure outside and inside is same,
So, net pressure is zero on the pistons.
So, Tension=0
(b)
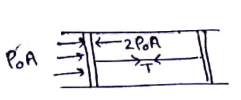
Net force on piston is zero
Solution 42
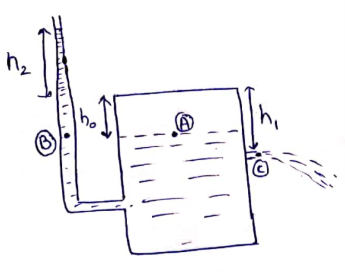
(a) 
(b) Applying Bernoulli's at A and C
(c) If water stops
coming out then pressure on horizontal line passing through hole will be 
. So, in long vertical
no water must be present above this line as it is open to atmosphere. Height
of water in long tube above the top is 
Solution 43
No. of moles initially=No. of moles finally
l=2.2m
Solution 44
No. of moles initially=No. of moles finally
cm
Solution 45
Here , 
P=84 cm of Hg
Kinetic Theory of Gases Exercise 37
Solution 46
Temperature is 20
and relative humidity is 100%, So
air is in saturated condition.
Dew point is the temperature at which SVP is equal to present vapour pressure.
So, 20 is the dew point.
Solution 47
Pa
When vapours are removed VP reduces to zero.
Net pressure inside the
room now=
=
KPa
≈102 KPa
Solution 48
Air becomes saturated at 10.
If room temperature falls to 15℃
then also dew point=10.
Solution 49
The point where the vapor starts, condensing VP=SVP.
Since, the process is isothermal.
Solution 50
76 cm of Hg
Now, when water is introduced the water vapor exerts some pressure against atmospheric pressure.
Pressure of vapor=76-75.4
=0.6 cm of Hg
Solution 51
At pressure of 760 mm we
drop perpendicular on temperature axis, So, T=65
Similarly, at 0.5 atm, T=48
Solution 52
Temperature of body=
=
=36.7
From graph, pressure
corresponding to temperature 36.7 is 50 mm of Hg.
Solution 53
Dew point=10
At 20, SVP=17.5 mm of Hg
At 10 (dew point), SVP=8.9 mm of Hg
=51%
Solution 54
At 30, 
of air contains 30
gm of water vapour
In 
air, water vapour=
=1500 gm
At 20℃, of air contains 16
gm of water vapour
In air, water vapour=
=800 gm
Amount of water vapour condensed=1500-800=700 gm
Solution 55
76 cm of Hg
SVP=0.8 cm of Hg
When water is introduced into the barometer, water evaporates and exerts pressure on mercury meniscas.
Pressure is minimum when the vapour reaches at saturation.
Net length of Hg column at SVG=76-0.8
=75.2 cm
Solution 56
Pressure exerted by 
vapour=
V.P
=99.4KPa-3.4KPa
=96kPa
Using, PV=nRT
96×
Solution 57
Let length of barometer tube be x
Initially,
1 cm of Hg
Later
0.9 cm of Hg
Now,
X=91.1 cm
Solution 58
At 0,
1.84 mm of Hg
Using PV=nRT;
1.97
RH=10.9%
Solution 59
VP=1800 Pa
Extra pressure required for saturation=3600-1800=1800 Pa
Let mass of vapour required be m for extra pressure
m=13 gm
Solution 60
VP=660 Pa
Now,
PV=nRT
m=238.5 gm
m≈238 gm
Solution 61
VP=660 Pa
Pressure for evaporated water is given by
1385 Pa
Net pressure=VP+
=660+1385
=2045 Pa
= 61.9%
R.H≈62%
Solution 62
(a) 
VP=0.64 kPa
Evaporation occurs as long as the atmosphere is not saturated.
Net pressure change= (1.6-0.64) kPa
= 0.96 kPa
Let mass of water evaporated be m. Then,
PV=nRT
m=361.45 gm
m≈361 gm
(b) At 20, SVP=2.4 KPa
At 15, SVP=1.6 KPa
Net pressure change=2.4-1.6=0.8 KPa
Mass of water evaporated
PV=
m=296 gm
