Class 12-science H C VERMA Solutions Physics Chapter 8 - Gauss' Law
Gauss' Law Exercise 141
Solution 1
(As given plane is parallel to YZ plane)
And flux is given as :
Solution 2
Linear charge density,
And charge enclose inside is given as:
Solution 3
Electric field is uniform and given plane is perpendicular to it. Thus it is an equipotential surface with no net current on that surface. So, net charge is :
Q = 0
Solution 4
If
Also,
Solution 5
By Gauss Law:
At centre of cube:
(For six surfaces)
Solution 6
Let us assume a cubical surface of side 'a'. So charge will be at centre of the cube and flux through one surface of cube is given as:
Solution 7
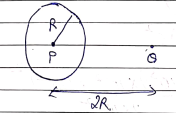
By gauss's law sphere experiences flux only by charge present inside sphere and not by charge present outside sphere.
Solution 8
In case of sphere flux is given as:
In case of hemisphere,
Solution 9
Volume charge density = 
We know,
Also,
Solution 10
(a) We know,
(b) Now,
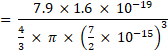
Also,
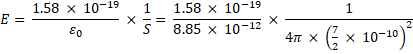
Solution 11
Charge enclosed by sphere of radius 
is :
By Gauss law,
Gauss' Law Exercise 142
Solution 12
By Property of induction charge
induced at inner surface 
and outer surface .→ +Q
(a) Surface charge density at inner
surface 
Surface charge density at outer
surface 
(b) When q is added then there is no effect on inner surface charge density
But when q is added outer surface charge density becomes,
(c) Let us assume an area inside
sphere which is at 
distance from centre of sphere.
Solution 13
(a) Electric field ,
(b) Total Charge Q = 
Electric field ,
Solution 14
We know,
Solution 15
For cylinder
Also, Force
Solution 16
We know,
(Total charge As nQ
= 
where, 
is volume charge density)
Solution 17
We know,
Solution 18
We know in case of charge conducting sheet:
And Force is :
=
0.45 N
Solution 19
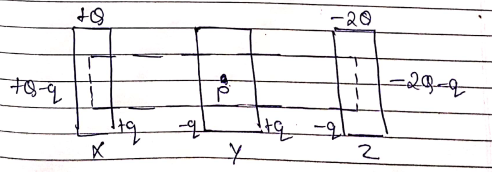
According to given figure:
And
Also
From (1) and (2)
Solution 20
(a) In equilibrium,
(b) For this, acceleration is included. Thus,
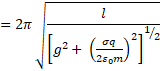
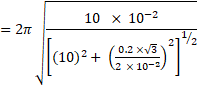
Solution 21
We know,
Now, electric field is given as:
And
Also
Solution 22
(a) For any point on left plate, electric flux is not present as it is outside the system. Hence, electric field,
E = 0
(b) For charge present in between plates, it experiences force towards negative plate, which is given as:
(c) For any point of right plate no electric flux is present as it is outside the system. Hence, electric field is given as:
E = 0
Solution 23
(a) Electric field at left end 
And Electric field at right end 
As the electric field is balanced
And 
(b) From above part,
(for left part)
As is charged plate 
electric field is directed towards left.
(c) Here, is charged plate so it acts as only source
of electric field. Thus, electric field is directed from left to right and is
given as:
(d) Similar to above part, Y acts as positive plate thus it repels, so electric field is directed towards right and is given as:
Solution 24
Net electric field at point P is:
Solving we get,
And, Net charge on right of right plate is:
