Class 12-science H C VERMA Solutions Physics Chapter 16 - Electromagnetic Induction
Electromagnetic Induction Exercise 306
Solution 1
(a) 
b) 
c) 
Solution 2
a) 
Unit 
c
b) |Emf| = 
= 
= 2at+b
= 2 (0.2) (2) + 0.4
= 1.2V
Solution 3
a)
Flux at 10ms 
= B.A = (0.01) (2 ×
Flux at 20ms 
=
B.A = (0.03) (2 ×
Flux at 30ms 
=
B.A = (0.01) (2 ×
Flux at 40ms 
=
B.A = (0.00) (2 ×
0ms to 10ms 
10ms to 20ms 
20ms to 30ms 
30ms to 40ms 
b) 
.
So, 
is not constant in 10ms to 30ms as slope is
not constant.
Solution 4
= 7.8 ×
Solution 5
Magnetic field due to
straight wire 
Solution 6
(a) 
= 
b) 
= 
c) 
Δ∅= 0
So,
V
Solution 7
(a) 
b)
c) Heat is a scalar quantity
= 25 + 25 = 50J
Solution 8
= -
= - (0.2) (5×
= 15 ×
a) For maximum ε
b) 
V
c) 
Solution 9
= (0.1) (1×
= 
= 
Emf =10μV
Solution 10
Δ∅= 
20 ×
= 
B = 5T
Solution 11
Charge flown = 
= 
ΔQ
= 
Solution 12
Δ∅= 4
Δ∅= -
Solution 13
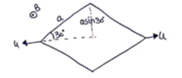
a) emf induced in one
side of rod 
= 
For four sides,
Emf induced will be
= 2Bua
b) V = IR
c) ΔQ = 
= 
ΔQ=
Electromagnetic Induction Exercise 307
Solution 14
= -1 volt
Solution 15
No flux change occurs. So emf induced is zero.
Solution 16
=
a) 
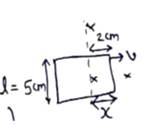
b) At t=10 sec, the loop is completely inside magnetic field, so magnetic flux does not change, so induced emf=0.
c)
d)At t=30, loop is completely
outside, so 
Solution 17
From time t=0 to t=5 sec and from t = 20sec to t=25sec heat will be produced.
I = 
Heat produced = 
=
= 
Solution 18
= 
Solution 19
a)
b)
c) No current as circuit is open
d) If 
are
closed, the circuit forms balanced wheat stone symmetry so,
i =0
Solution 20
The magnetic field due to coil of
radius a at a distance of 
is
So, flux linked with coil of radius a'
∅= B.A =
Now, let y be the distance of the sliding contact from its left end, so
Resistance of Rheostat R' = 
Current i = 
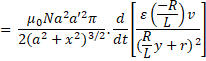
a) For
b) For 
Solution 21
a) 
= 
b) 
∆Q = 
∆Q =
1.57×
Solution 22
a) 
Time to rotate coil by half turn
ω=
300 ×
=
t= 
= 
= 
b) For full turn
So, Δ∅= 0
Hence 
c) 
ΔQ=
ΔQ
= 5 ×
Solution 23
Charge flown ΔQ=
= 
ΔQ=
4.7 ×
Solution 24
=
For N- Turns
a) Maximum 
= (0.01) (π)×
= 6.66 ×
b) Average value of 
so, 
c) 
Average value of 
Electromagnetic Induction Exercise 308
Solution 27
(a) F = Q (
)
= (1.6 ×
F= 1.6 ×
(b) 
E = (0.1) (0.1) sin90
E = 
It is created due to motional emf.
c) ε= 
= (0.1) (0.2) (0.1)
ε= 2 ×
Solution 25
Heat = 
= 
= 
= 
= 
H= 1.3 ×
J
Solution 26
= (2×
)
0
Solution 28
ε=
= (0.2) (1) (2)
ε=
0.4
Solution 29
ε=
= (3×
( 3×
)(10)
ε= 9
×
Solution 30
ε= 
= (0.2×
(
180×
)(1)
ε=
ε= 
Solution 31
ε=
a) Loop abc
l = distance between initial and final points of wire perpendicular to B and V
here l = 0 [ ∵ closed loop]
so, 
b) segment bc
with
positive polarity at point c
c) Segment ac
d) Segment ab
length component of ab
perpendicular to 
is bc
with
positive polarity at point a
Solution 32
a)
b)
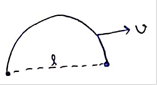
[∵l is parallel to v]
Solution 33
= (1)
(0.2)
ε ≄17 ×
Solution 34
a) 𝛆mf maximum is between PQ
b) 𝛆mf
maximum is between AB as 
ε=0
Solution 35
As circuit is open, So current flows in the wire
∴ 
Solution 36
Emf induced = 
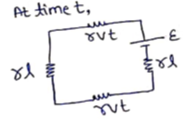
wire travels distance 
in time t
So, resistance = 
Current = 
= 
Solution 37
a) Force by magnetic field
Since wire moves with constant velocity
b) At t=0
Let time = t at which
force becomes 
Electromagnetic Induction Exercise 309
Solution 38
a) 
I = 
b) Force on the wire 
F = B 
(Retardation)
c) a = 
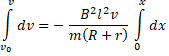
V = 
d) let rod stops after x distance so, v = 0
0 = 
Solution 39
a) 
= (0.02) (v) (0.08)
= 16v ×
Current in loop = 
= 
I = 8v ×
Force by magnetic field = external force
b) ϵmf = 16v ×
= 16 (25) ×
= 4 ×
c) Potential difference between ab
= ×
d) Resistance of wire cd = 
Current = 8(25) ×
= (2×
= 4 ×
V
Solution 40
ε= 
IR=
(2×
tan𝛅
= 
Solution 41
ε
I = 
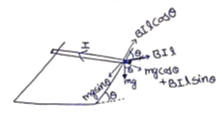
Since, red moves with
constant velocity, 
Tesla
Solution 42
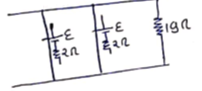
(a) Induced emf in each
wire=
= (1) (0.05) (0.04)
=
V
Both are in parallel combination.
For cell:-
V
of circuit=19+1=20Ω
Current=
A
(b) Polarity of cell will be reverse of each other.
So, net emf is zero.
∴Current=0
Solution 43
(a)
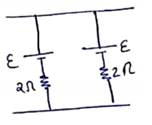
[As both opposes each other]
Current=0
(b)
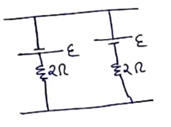
Current
Solution 44
(a) emf=
=
emf=
V
I=
A
(b) emf=
=
emf=V
I=
Solution 45
Initially, current
passing through each wire is 
(from c to d)
Now, motional Emf due to wire ab=Blv
Hence, current flown=
(from d to c)
By superposition principle
Net current flown in
wire cd=
=
Solution 46
Force on wire
Initial velocity, u=0
Solution 47
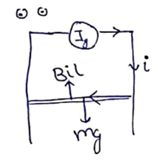
Initially body is in equilibrium
Now wire of double mass is placed
Using,
Electromagnetic Induction Exercise 310
Solution 48
(a)
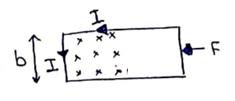
Emf induced =
Force due to induced
current= 
=
(in right direction)
Net force=
(b) As velocity increases, acceleration decreases and when a=0, constant velocity is attained.
(c) 
Solution 49
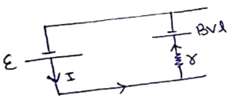
(a) Motional emf
induced=
=
(b) Force=
=
towards right
(c) Since force is in direction of velocity. So, velocity increases and hence force decreases.
When F=0, it attains
constant velocity 
Solution 50
(a) emf induced=
=
(b) emf=
(from b to a as per Lenz law)
(c) 
(d) When a=0, wire
attains constant velocity 
(e) 
(f) 
(g) Rate of heat=Power developed =Voltage × Current
=
=
Rate of potential energy
So,
(Hence proved)
Solution 51
V
Solution 52
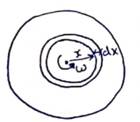
Emf in elemental Ring
Solution 53
I=0.5 mA
Centre is at higher Potential. So, current leaves the center.
Solution 54
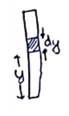
Emf induced in the element
Solution 55
Emf induced in element =
Electromagnetic Induction Exercise 311
Solution 56
(a) To move with constant velocity, force on element dr
(b) 
(c) 
(d) 
Rate
of heat developed by resistor
Solution 57
(a) Flux through small strip
(b) Emf=
(c) Heat=
Solution 58
By Faraday's Law:-
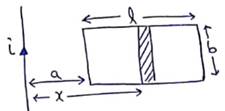
Flux in small strip
Emf=
Emf=
By motional Emf:-
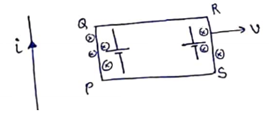
Emf for PQ=
=
Emf for QR=0 [
]
Emf for RS =
Emf for SP=0 []
Solution 59
Emf induced =
Current, 
=force by magnetic field
Solution 60
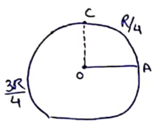
Both the segments are in parallel combination
Emf induced=
Solution 61
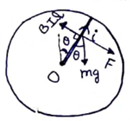
Emf induced =
Current
Torque about 0
Here 
,
as it rotates with uniform velocity
Solution 62
Induced Emf=
∵Angular velocity is constant
(about 0)
Solution 63
Potential difference across capacitor is equal to motional emf of rod.
[q and v are assumed charge and
velocity of rod]
Current, 
Net force on wire
Solution 64
(a) Emf=
(b) For square loop
Emf=
Electromagnetic Induction Exercise 312
Solution 65
(a) Initially, let current be i inside the solenoid
After t=2 seconds, current in solenoid =i+0.01×2
=i+0.02
Wb
(b) 
V/m
Solution 66
Emf=
L=0.4H
Solution 67
H
Solution 68
Self-inductance of
solenoid 
H
Emf=
V
Solution 69
(a) 
(b) 
(c) 
Solution 70
Resistance of the coil, 
Time constant, 
sec
Solution 71
(a) 
I=0.17A
(b) Magnetic energy=
Solution 72
L=4H
Solution 73
V
Solution 74
(a) 
I=0.44A
(b) 
I=0.79A
(c)
I=1.8A
(d) 
I=2A
Solution 75
(a) At t=100ms
(b) At t=10ms
(c) At t=1sec
Solution 76
Emf=
(a) Emf=0.27V
(b) Emf=0.036V
(c) Emf=
V
Solution 77
(a) At t=0
=2500 V/sec
(b) At t=10ms
=17 V/s
(c) At t=1sec
0
V/s
Solution 78
(a) At t=20ms
V=3.16 Volt
(b) At t=100ms
V=4.97 Volt
(c) At t=1sec
V=5 Volt
Solution 79
(a) At t= 10ms= 0.01sec
C
(b) At t= 20ms= 0.02sec
mC
(c) At t= 100ms= 0.1 sec
Q=5.7mC
Solution 80
Resistance, 
R=1.7Ω
Time constant,
Solution 81
(a) 
Now,
Taking ln on both sides
t=35ms
(b) Maximum Power
dissipated=
Power dissipated at time 't' =
t=61ms
(c) Energy store at
time t =
(Maximum energy stored)
t=61ms
Solution 82
Energy stored in time 
=
Maximum energy stored
Energy stored in time 
= Maximum energy stored
Now, 
Solution 83
(a) 
Τ=0.4sec
(b) 
t=τ
t=0.4sec
(c) At t=τ
I=0.25A
Power delivered by battery, P=VI
= (4) (0.25)
P=1W
(d) Power dissipated=
=
≈0.64W
Solution 84
R≈160Ω
Solution 85
(a) 
(b) Work done by battery=charge × voltage
(c) Heat=
(d) 
(e) Work done = Energy stored + Heat loss
=
Work done =
Solution 86
(a)
I=6.3mA
(b) Power delivered =VI
= (2) (
)
P=12.6mW
(c) Power dissipated
P=8mW
(d) Rate at which energy
is stored 
=4.6mW
Solution 87
(a) At t=100ms=0.1 sec
(b) At t=200ms=0.2 sec
(c) At t=1sec
Solution 88
(a)
sec
(b) 
R=28Ω
Electromagnetic Induction Exercise 313
Solution 89
Let 
be constant current in circuit initially.
Charge flown in one time constant.
Now, battery is removed.
So, current in circuit,
Total charge flown=
Hence proved.
Solution 90
(a) At 
,
inductor will behave as conducting wire
(b) Time constant 
(c)
Solution 91
J
Solution 92
Magnetic field at the center of the circular loop
T
J
Solution 93
Magnetic field due to
wire, 
J
Solution 94
Emf
Volt
Solution 95
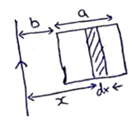
Magnetic flux linked to small element
Also, 
Solution 96
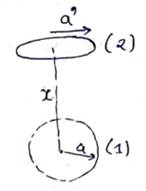
Magnetic field due to coil1 at the center of coil2 is
Flux linked with coil2 is
Now, mutual inductance
Solution 97
Magnetic field due to
solenoid having 2000 turns=
Flux linked with
solenoid having 4000 turns 
iWb
[Here N=2000 as flux is linked in only 10cm of length of solenoid]
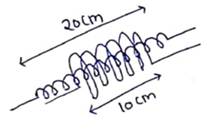
Mutual inductance
H
Solution 98
(a) Emf
Emf
(b) Flux linked with the secondary coil
Mutual inductance
