JEE Plances Class Answered

Asked by Tanishq | 07 May, 2018, 07:24: AM

Expert Answer

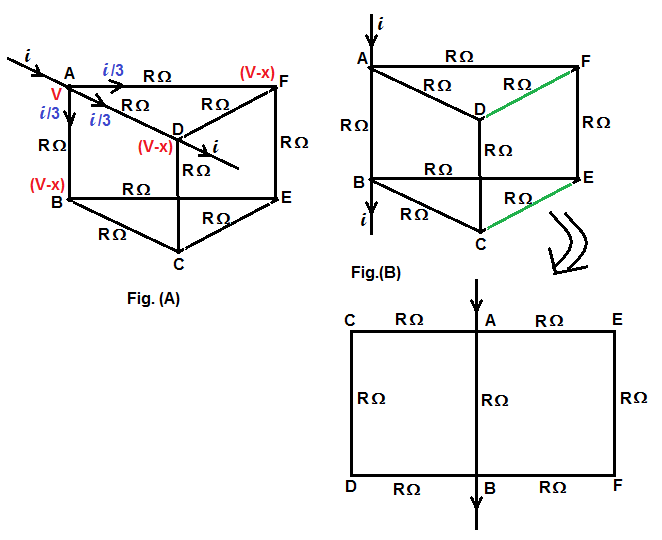
(1) Equivalent resistance across AD

As shown in fig.(A), let us assume a current of i at A is entering the given network and leaving at D. By symmetry the current i is divided into three equal parts i/3 and equal currents are flowing through AB, AD and AF. Let V volts be the potential at point A and at points B,d and F let the potential be (V-x) volts.

Hence across AD we have potential drop x volts which is given by x = (i/3)×R, then equivalent resistace is (R/3) ohms

(2) Equivalent resistance across AB

As shown in fig.(B), let us assum a current of i at A is enetering the given network and leaving at B. By symmetry equal currents flow through AF and AD. Hence D and F are equi-potential points. There will not be any flow through DF (shown in figure as green). Similarly by symmetry, equal current flows from C to B and also from E to B. Hence C and E are equi-potential points. There will not be any current flow along CE(shown in figure as green). Using these conditions, the given network is unfolded as shown in fig.(B). Now AC,CD anf DB are in series and resistance of path AC+CD+DB is 3R Ω. Similarly the path AE+EF+FB has resistance 3R Ω. The equivalent resistance is parallel combination of 3R Ω, R Ω and 3R Ω, which is (3/5)R Ω

Answered by Thiyagarajan K | 08 May, 2018, 13:51: PM

Please Login or Sign up to continue!

JEE Plances Class Answered

Choose Filters

Open In Ask A Doubt App ?

Get in Touch

Call / Whats App