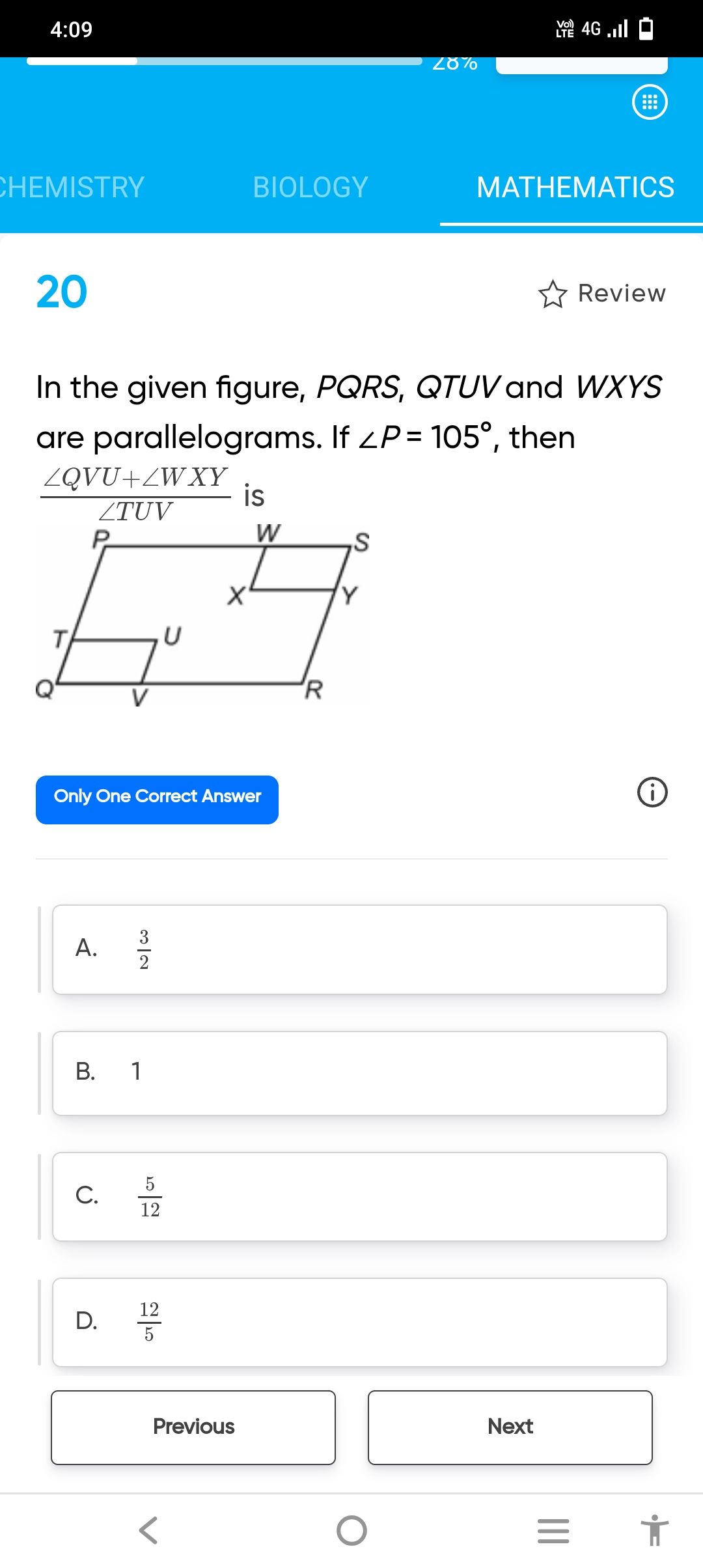
CBSE Class 9 Answered
ABCD is a quadrilateral in which P,Q,R and S are mid points of sides AB BC CD DA
show that PQRS IS A PARALELLOGRAM
Asked by Sanmit Ratnaparkhi | 19 Mar, 2014, 11:48: PM
ABCD is a quadrilateral.
P, Q, R, S are the mid points of sides AB, BC, CD and DA.
Join Diagonal AC.
Consider triangle ABC.
Here, P and Q are the mid points of sides AB and BC respectively.
So, by using the mid point theorem we can say that PQ is parallel to AC.
Similarly RS can be shown parallel to AC.
So, we have PQ parallel to RS (as both are parallel to AC)
In the same way you can join diagonal BD and show that PS is parallel to QR.
So we have a quadrilateral PQRS in which both pairs of opposite sides are parallel. SO, it becomes a parallelogram.
Answered by | 20 Mar, 2014, 10:12: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM