NEET1 Class Answered
A block of mass m is placed at relative equilibrium on an inclined plane which itself is placed on a lift moving upwards with constant velocity 
. If the friction coefficient between block and plane is 
, find the instantaneous power supplied by friction to the block??
a) 
mgsin (2
)/2 , b) mg sin^2
, c) mgsin(2)/2 , d) mgcos^2
. If the friction coefficient between block and plane is , find the instantaneous power supplied by friction to the block??
a) mgsin (2)/2 , b) mg sin^2, c) mgsin(2)/2 , d) mgcos^2
Asked by patra04011965 | 26 Sep, 2018, 22:15: PM
Expert Answer
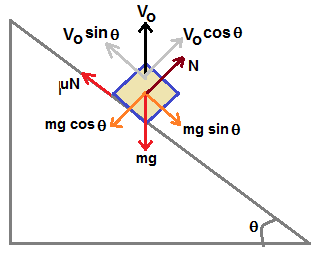
Figure shows the forces acting on the the block placed on an inclined plane.
Figure also shows the velocity vector V0 due to lift movement along with the resolved components.
Power due to force = Force×velocity = F·V , where F and V are vectors and power is expressed in terms of dot product or scalar product.
Here force is friction force F = μ×N = μ×m×g×cosθ
velocity component in the direction of friction force = V0×sinθ
hence power = μ×m×g×cosθ × V0×sinθ = (1/2)×μ×V0×m×g×sin(2θ)
Answered by Thiyagarajan K | 27 Sep, 2018, 11:23: AM
NEET1 - Physics
Asked by nasir.mirza | 15 Dec, 2018, 11:37: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by nasir.mirza | 15 Dec, 2018, 11:27: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by nasir.mirza | 15 Dec, 2018, 11:27: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by nasir.mirza | 15 Dec, 2018, 11:26: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by nasir.mirza | 15 Dec, 2018, 11:24: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by avinashbabu143143143 | 15 Dec, 2018, 10:39: AM
ANSWERED BY EXPERTNEET1 - Physics
Asked by Deepak | 11 Dec, 2018, 12:37: PM
ANSWERED BY EXPERTNEET1 - Physics
Asked by sahu.mithun07 | 10 Dec, 2018, 23:23: PM
ANSWERED BY EXPERTNEET1 - Physics
Asked by kuldeepaish8601 | 01 Dec, 2018, 20:13: PM
ANSWERED BY EXPERTNEET1 - Physics
Asked by mvenkataram | 01 Dec, 2018, 03:50: AM
ANSWERED BY EXPERT
