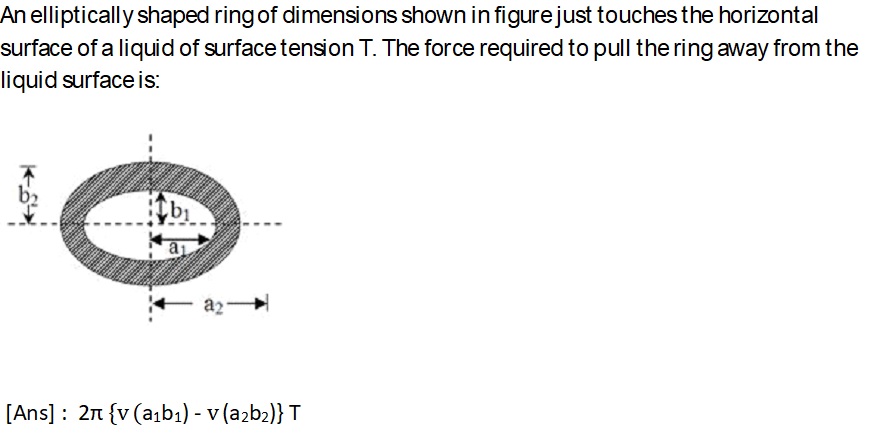
JEE Plances Class Answered

Asked by rbhatt16 | 19 Jul, 2018, 09:26: AM

Expert Answer

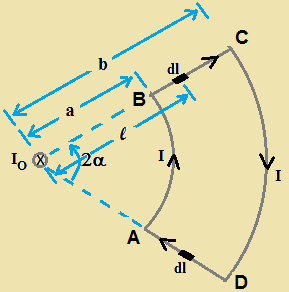
A loop ABCD carrying current I is placed near a wire that carrying current I₀ inwards as shown in figure.

Magnetic field produced by the current carrying wire at segments AB and CD is parallel to the current flow in the loop.

Hence in the segments there will not be force due to magnetic field.

But in segments BC and AD force will be generated due to the current flow in the loop and

magnetic field produced by the current carrying wire.

Let dl be a small current element in segment BC which is at a distance l from wire as shown in figure.

Force dF on current element dl is given by , dF= B×I×dl ..................(1)

where B is magnetic field due to current carrying wire and B is given by,

begin mathsize 12px style B space equals space fraction numerator mu subscript 0 space I subscript 0 over denominator 2 pi space l end fraction end style

Hence we have,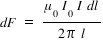

begin mathsize 14px style d F space equals space fraction numerator mu subscript 0 space I subscript 0 space I space d l over denominator 2 pi space l end fraction end style

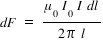........................(2)

Similarly we can consider a small current element dl in segment AD and get the force as given in eqn.(2)

These two forces acting as a couple and torque dτ due to this couple is given by

dτ = 2lsinα × dF =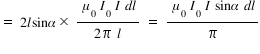

begin mathsize 14px style equals space 2 l sin alpha cross times space fraction numerator space mu subscript 0 space I subscript 0 space I space d l over denominator 2 pi space l end fraction space equals space fraction numerator space mu subscript 0 space I subscript 0 space I space sin alpha space d l over denominator pi end fraction end style

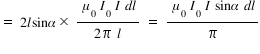..........(3)

Total torque τ on the loop is given by,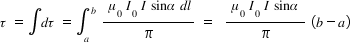

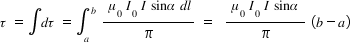
begin mathsize 14px style tau space equals integral d tau space equals integral subscript a superscript b space fraction numerator space mu subscript 0 space I subscript 0 space I space sin alpha space d l over denominator pi end fraction space equals space space fraction numerator space mu subscript 0 space I subscript 0 space I space sin alpha space over denominator pi end fraction space left parenthesis b minus a right parenthesis end style

Answered by Thiyagarajan K | 21 Jul, 2018, 14:41: PM

Please Login or Sign up to continue!