CBSE Class 10 Answered
Question 1)
Find the sum of the first 24 terms of the list of numbers whose nth term is given (3+2n).
Question 2)
For what value of n , are the nth terms of the two AP 63,65,67 and 3,10,17........ are equal ?
Question 3)
The pth term of an AP is a and qth term is b . Prove that the sum of its (p+q) terms = p+q/2{ a+ b+ (a-b/p-q)}.
Asked by arindeep.singh | 22 Jul, 2020, 18:24: PM
(1)
an= 3+2n
Now, put n=1,2,3,...
a1= 3+2(1) = 5
a2= 3+2(2) = 7
a3= 3+2(3) = 9
Thus, the terms of the AP are 5,7,9,....
Here, a = 5 and d = 2
S24= [25+(24 -1)2]
= 12[10+46]
= 12 56
= 672
(2)
In the first AP, a = 63 and d = 2
In the second AP, a = 3 and d = 7
As the nth term of both APs be equal
63+(n-1)2 = 3+(n-1)7
63+2n-2 = 3+7n-7
61+2n = 7n-4
5n = 65
n = 13
Hence, the 13th term of the APs are equal.
3)
pth term is a and qth term is b
A + (p - 1)D = a ... (1)
A + (q - 1)D = b ... (2)
Subtracting (2) from (1), we get
(p-1-q+1)D = a-b
D = a-b/p-q
Adding (1) and (2), we get
2A + D(p+q-2) = a+b
2A + D(p+q-1) = a+b+D
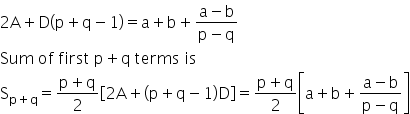
Answered by Renu Varma | 23 Jul, 2020, 12:32: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by sahooashutosh781 | 21 May, 2024, 13:26: PM
CBSE 10 - Maths
Asked by purbashadebnath1980 | 09 Mar, 2024, 12:10: PM
CBSE 10 - Maths
Asked by durgauikey7000 | 08 Dec, 2023, 20:16: PM
CBSE 10 - Maths
Asked by prassanna.j | 13 Nov, 2023, 23:23: PM
CBSE 10 - Maths
Asked by latayadav23 | 17 Oct, 2023, 20:25: PM
CBSE 10 - Maths
Asked by paresh0311 | 21 Mar, 2023, 16:58: PM
CBSE 10 - Maths
Asked by vaishaliboriwarruturushi | 16 Dec, 2022, 19:13: PM
CBSE 10 - Maths
Asked by jaiprakashprasadr | 19 Jul, 2022, 21:22: PM
CBSE 10 - Maths
Asked by harinimathi815 | 21 Feb, 2022, 20:14: PM
CBSE 10 - Maths
Asked by monalipradhan909 | 21 Mar, 2021, 19:10: PM











