CBSE Class 9 Answered
give me the solutions of the exercise 8.1
Asked by paddipawar | 02 Dec, 2014, 09:22: PM
12.
Extend AB. Draw a line through C, which is parallel to AD, intersecting AE at point E.
Now, AECD is a parallelogram.
Now, AECD is a parallelogram.
(i) AD = CE (opposite sides of parallelogram AECD)
But AD = BC (given)
So, BC = CE
 CEB =
CEB =  CBE (angle opposite to equal sides are also equal)
CBE (angle opposite to equal sides are also equal)
Now consider parallel lines AD and CE. AE is transversal line for them
 A +
A +  CEB = 180 (angles on the same side of transversal)
CEB = 180 (angles on the same side of transversal)
 A+
A+  CBE = 180 (using the relation
CBE = 180 (using the relation CEB =
CEB =  CBE) ... (1)
CBE) ... (1)
But B +
B +  CBE = 180 (linear pair angles) ... (2)
CBE = 180 (linear pair angles) ... (2)
From equations (1) and (2), we have
 A =
A =  B
B
(ii) AB || CD
 A +
A +  D = 180 (angles on the same side of transversal)
D = 180 (angles on the same side of transversal)
Also C +
C +  B = 180 (angles on the same side of transversal)
B = 180 (angles on the same side of transversal)
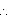
 A +
A +  D =
D =  C +
C +  B
B
But AD = BC (given)
So, BC = CE
 CEB =
CEB =  CBE (angle opposite to equal sides are also equal)
CBE (angle opposite to equal sides are also equal) Now consider parallel lines AD and CE. AE is transversal line for them
 A +
A +  CEB = 180 (angles on the same side of transversal)
CEB = 180 (angles on the same side of transversal) A+
A+  CBE = 180 (using the relation
CBE = 180 (using the relation CEB =
CEB =  CBE) ... (1)
CBE) ... (1) But
 B +
B +  CBE = 180 (linear pair angles) ... (2)
CBE = 180 (linear pair angles) ... (2) From equations (1) and (2), we have
 A =
A =  B
B (ii) AB || CD
 A +
A +  D = 180 (angles on the same side of transversal)
D = 180 (angles on the same side of transversal) Also
 C +
C +  B = 180 (angles on the same side of transversal)
B = 180 (angles on the same side of transversal)  A +
A +  D =
D =  C +
C +  B
BBut
 A =
A =  B [using the result obtained proved in (i)]
B [using the result obtained proved in (i)] C =
C =  D
D (iii) In ABC and BAD
AB = BA (common side)
BC = AD (given)
 B =
B =  A (proved before)
A (proved before)  ABC
ABC 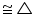 BAD (SAS congruence rule)
BAD (SAS congruence rule) (iv)
 ABC
ABC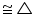 BAD
BAD 11.
(i) Here AB = DE and AB || DE.
Now, if two opposite sides of a quadrilateral are equal and parallel to each other, it will be
Now, if two opposite sides of a quadrilateral are equal and parallel to each other, it will be
a parallelogram.
Therefore, quadrilateral ABED is a parallelogram.
(ii) Again BC = EF and BC || EF.
Therefore, quadrilateral BEFC is a parallelogram.
Therefore, quadrilateral ABED is a parallelogram.
(ii) Again BC = EF and BC || EF.
Therefore, quadrilateral BEFC is a parallelogram.
(iii) Here ABED and BEFC are parallelograms.
AD = BE, and AD || BE
(Opposite sides of parallelogram are equal and parallel)
And BE = CF, and BE || CF
(Opposite sides of parallelogram are equal and parallel)
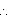 AD = CF, and AD || CF
AD = CF, and AD || CF
(iv) Here one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and
AD = BE, and AD || BE
(Opposite sides of parallelogram are equal and parallel)
And BE = CF, and BE || CF
(Opposite sides of parallelogram are equal and parallel)
(iv) Here one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and
parallel to each other,
so, it is a parallelogram.
(v) As ACFD is a parallelogram, so, pair of opposite sides will be equal and parallel to each
so, it is a parallelogram.
(v) As ACFD is a parallelogram, so, pair of opposite sides will be equal and parallel to each
other.
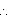 AC || DF and AC = DF
AC || DF and AC = DF
(vi)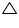 ABC and
ABC and 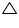 DEF.
DEF.
AB = DE (given)
BC = EF (given)
AC = DF (ACFD is a parallelogram)
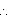
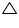 ABC
ABC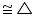 DEF (by SSS congruence rule)
DEF (by SSS congruence rule)
(vi)
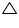 ABC and
ABC and  DEF.
DEF.AB = DE (given)
BC = EF (given)
AC = DF (ACFD is a parallelogram)
 ABC
ABC DEF (by SSS congruence rule)
DEF (by SSS congruence rule)10.
(i) In  APB and
APB and 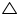 CQD
CQD
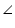 APB =
APB = 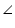 CQD (each 90o)
CQD (each 90o)
AB = CD (opposite sides of parallelogram ABCD)
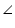 ABP =
ABP = 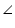 CDQ (alternate interior angles for AB || CD)
CDQ (alternate interior angles for AB || CD)
 APB
APB 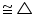 CQD (by AAS congruency)
CQD (by AAS congruency)
(ii) By using the result obtained as above
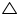 APB
APB 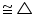 CQD, we have
CQD, we have
AP = CQ (by CPCT)
9.
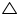 APB and
APB and 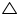 CQD
CQD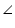 APB =
APB = 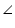 CQD (each 90o)
CQD (each 90o) AB = CD (opposite sides of parallelogram ABCD)
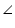 ABP =
ABP = 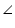 CDQ (alternate interior angles for AB || CD)
CDQ (alternate interior angles for AB || CD) 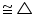 CQD (by AAS congruency)
CQD (by AAS congruency) (ii) By using the result obtained as above
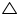 APB
APB 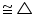 CQD, we have
CQD, we have AP = CQ (by CPCT)
9.
(i) In  APD and
APD and  CQB
CQB
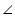 ADP =
ADP = 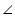 CBQ (alternate interior angles for BC || AD)
CBQ (alternate interior angles for BC || AD)
AD = CB (opposite sides of parallelogram ABCD)
DP = BQ (given)
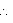
 APD
APD 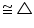 CQB (using SAS congruence rule)
CQB (using SAS congruence rule)
(ii) As we had observed that APD
APD 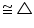 CQB
CQB
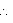 AP = CQ (CPCT)
AP = CQ (CPCT)
 APD and
APD and  CQB
CQB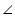 ADP =
ADP = 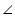 CBQ (alternate interior angles for BC || AD)
CBQ (alternate interior angles for BC || AD) AD = CB (opposite sides of parallelogram ABCD)
DP = BQ (given)
 APD
APD 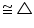 CQB (using SAS congruence rule)
CQB (using SAS congruence rule) (ii) As we had observed that
 APD
APD 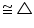 CQB
CQB (iii) In  AQB and
AQB and  CPD
CPD
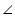 ABQ =
ABQ = 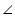 CDP (alternate interior angles for AB || CD)
CDP (alternate interior angles for AB || CD)
AB = CD (opposite sides of parallelogram ABCD)
BQ = DP (given)
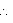
 AQB CPD (using SAS congruence rule)
AQB CPD (using SAS congruence rule)
(iv) As we had observed that AQB
AQB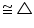 CPD
CPD
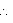 AQ = CP (CPCT)
AQ = CP (CPCT)
 AQB and
AQB and  CPD
CPD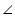 ABQ =
ABQ = 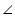 CDP (alternate interior angles for AB || CD)
CDP (alternate interior angles for AB || CD)AB = CD (opposite sides of parallelogram ABCD)
BQ = DP (given)
 AQB CPD (using SAS congruence rule)
AQB CPD (using SAS congruence rule) (iv) As we had observed that
 AQB
AQB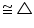 CPD
CPD (v) From the result obtained in (ii) and (iv), we have
AQ = CP and AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other. So, APCQ is a
parallelogram.
You have not mentioned the book for which you want to get the solutions
We have provided solutions of 9,10,11,12 of Ex.8.1 of NCERT.
If you need all the solutions, please enroll for textbook solutions from topper's site.
Answered by Vimala Ramamurthy | 03 Dec, 2014, 08:52: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM