CBSE Class 9 Answered
Find the degree of the given polynomials
(i) 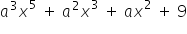
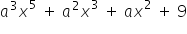
(ii) 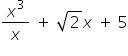
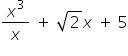
(iii)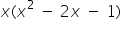
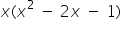
(iv)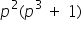
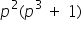
Asked by vatsalchoudhary41 | 29 Jun, 2014, 11:22: AM

Answered by Vijaykumar Wani | 30 Jun, 2014, 10:27: AM
Concept Videos
CBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
CBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
CBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
CBSE 9 - Maths
Asked by dpsvijender | 21 Jun, 2022, 10:37: AM
CBSE 9 - Maths
Asked by vandanagarwal28 | 18 Jun, 2022, 05:57: PM
CBSE 9 - Maths
Asked by vandanagarwal28 | 17 Jun, 2022, 03:53: PM
CBSE 9 - Maths
Asked by leeladhar6731 | 24 May, 2022, 10:36: PM
CBSE 9 - Maths
Asked by al3690092 | 22 May, 2022, 09:26: PM




