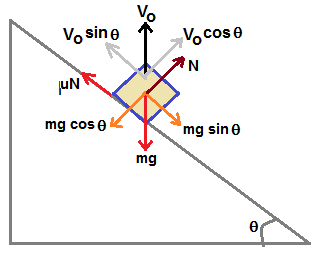
A block of mass m is placed at relative equilibrium on an inclined plane which itself is placed on a lift moving upwards with constant velocity 
a) 
Asked by patra04011965
26th September 2018,
10:15 PM
Answered by Expert
Answer:
Figure shows the forces acting on the the block placed on an inclined plane.
Figure also shows the velocity vector V0 due to lift movement along with the resolved components.
Power due to force = Force×velocity = F·V , where F and V are vectors and power is expressed in terms of dot product or scalar product.
Here force is friction force F = μ×N = μ×m×g×cosθ
velocity component in the direction of friction force = V0×sinθ
hence power = μ×m×g×cosθ × V0×sinθ = (1/2)×μ×V0×m×g×sin(2θ)
Answered by Expert
27th September 2018,
11:23 AM
Rate this answer
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer 9/10
Your answer has been posted successfully!
RELATED STUDY RESOURCES :
Browse free questions and answers by Chapters
- 1 Thermodynamics
- 2 Gravitation
- 3 Electromagnetic Waves
- 4 Communication Systems
- 5 Laws of Motion
- 6 Current Electricity
- 7 Work, Energy and Power
- 8 Kinematics
- 9 Physics and Measurement
- 10 Rotational Motion
- 11 Properties of Solids and Liquids
- 12 Kinetic Theory of Gases
- 13 Oscillations and Waves
- 14 Electrostatics
- 15 Magnetic Effects of Current and Magnetism
- 16 Electromagnetic Induction and Alternating Currents
- 17 Optics
- 18 Dual Nature of Matter and Radiation
- 19 Atoms and Nuclei
- 20 Electronic Devices
Trending Tags
Latest Questions
JEE Main Mathematics
Asked by amaladelsingh
28th October 2020,
10:24 PM
CBSE X Biology
Asked by reenacharan2008
28th October 2020,
9:11 PM
