Please wait...

Contact Us

Contact

Need assistance? Contact us on below numbers

For Study plan details

93219 24448 / 89292 63204

10:00 AM to 7:00 PM IST all days.

For Franchisee Enquiry

81783 72169

OR

Chat with us on WhatsApp

or

Customer Support

Home / Doubts and Solutions/NEET/Physics

The maximum vertical distance through which a fully dressed astronaut can jump on
the earth is 0.5 m. If mean density of the moon is two thirds that of the earth and
radius is one quarter that of the earth, the maximum vertical distance through which
he can jump on the moon and the ratio of time of duration of the jump

Asked by rushikeshyeole21 1st February 2018, 4:58 PM

Answered by Expert

Answer:

The required equation to solve this problem :- v² = u²-2gh . v is final speed in this case it is zero, when astronaut jumps and reaches maximum height his speed is zero. u is initial jumping speed. g is acceleration due to gravity and h is the maximum jumping height.

If jumping speed on earth and moon are assumed as same, then height is inversely proportional to acceleration due to gravity.

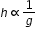
begin mathsize 12px style h proportional to 1 over g end style

now acceleration due to gravity

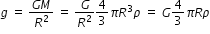
begin mathsize 12px style g space equals space fraction numerator G M over denominator R squared end fraction space equals space G over R squared 4 over 3 pi R cubed rho space equals space G 4 over 3 pi R rho end style

G - gravitational constant M mass of earth, ρ is mean density, R is radius

If we consider 2/3 of earth density as moon's density and 1/2 of earth radius as moon's radius

then acceleration due to gravity on moon,

begin mathsize 12px style g subscript M space equals 1 over 6 g subscript E end style

g_E is acceleration due to gravity on earth

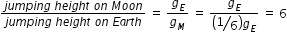
begin mathsize 12px style fraction numerator j u m p i n g space h e i g h t space o n space M o o n over denominator j u m p i n g space h e i g h t space o n space E a r t h end fraction space equals space g subscript E over g subscript M space equals space fraction numerator g subscript E over denominator open parentheses begin display style bevelled 1 over 6 end style close parentheses begin display style begin display style g end style subscript E end style end fraction space equals space 6 end style

Hence the astronaut will jump a height of 6 × 0.5 = 3 m on moon

Answered by Expert 1st February 2018, 6:01 PM

Rate this answer

1
2
3
4
5
6
7
8
9
10

You have rated this answer 10/10

Report an issue

Tags: gravitation acceleration-due-to-gravity

Previous Question

Your answer has been posted successfully!

Free related questions

weight of the body is zero in free fall why?

21st February 2022, 5:18 PM

difference between G , g

21st March 2022, 8:36 AM

if acceleration due to gravity g at height h

5th July 2022, 7:13 AM

what is the derivation of formula of gravity

30th July 2022, 8:09 PM

what is the weight of an object at the centre of the earth

9th August 2022, 8:52 PM

RELATED STUDY RESOURCES :

NEET QUESTION ANSWERS

Browse free questions and answers by Chapters

Latest Questions

CBSE X Biology

Asked by Sureshgowdayd548 28th October 2020, 10:50 PM

JEE Main Mathematics

The following pseudocode is executed using the “Paragraph words” dataset. At the end of the execution, CountB captures the number of verbs with letter count less than the average letter count of verbs. But the pseudocode may have mistakes in one or more lines. Identify all such lines (if any). It is a Multiple Select Question (MSQ). Error in Line 4 Error in Line 8 Error in Line 11 Error at Line 12 Error in Line 17 Error at Line 18 Error in Line 21 The following pseudocode is executed using the “Words” table. What will be the value of A at the end of the execution?

Asked by amaladelsingh 28th October 2020, 10:24 PM

CBSE X Biology

I want a brief clarity on Taxonomy

Asked by reenacharan2008 28th October 2020, 9:11 PM

Chat with us on WhatsApp