Class 10 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 1 - Linear Equations in Two Variables
Linear Equations in Two Variables Exercise Ex. 1.1
Solution 1
5x + 3y = 9 … (I)
2x - 3y = 12 … (II)
Let's add equations (I) and (II).
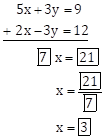
Place x = 3 in equation (I).
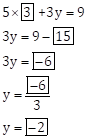
![]()
Solution 2(1)
3a + 5b = 26 … (I)
a + 5b = 22 … (II)
Let's subtract equation (II) from (I).
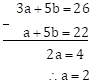
Substituting a = 2 in equation (II)
a + 5b = 22
∴ 2 + 5b = 22
∴ 5b = 22 - 2
∴ 5b = 20
b = 4
∴ Solution is (x, y) = (2, 4).
Solution 2(2)
x + 7y = 10 … (I)
3x - 2y = 7 … (II)
Multiplying equation (I) by 3.
∴ x × 3 + 7y × 3 = 10 × 3
∴ 3x + 21y = 30 … (III)
Subtracting equation (II) from equation (III).
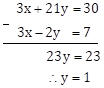
Substituting y = 1 in equation (II).
3x - 2y = 7
∴ 3x - 2×1 = 7
∴ 3x - 2 = 7
∴ 3x = 9
∴ x = 3
∴ Solution is (x, y) = (3, 1).
Solution 2(3)
2x - 3y = 9 … (I)
2x + y = 13 … (II)
Subtracting equation (I) from equation (II).
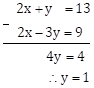
Substituting y = 1 in equation (I).
2x - 3y = 9
∴ 2x - 3×1 = 9
∴ 2x - 3 = 9
∴ 2x = 9 + 3
∴ 2x = 12
∴ x = 6
∴ Solution is (x, y) = (6, 1).
Solution 2(4)
5m - 3n = 19 … (I)
m - 6n = -7 … (II)
Multiplying equation (II) by 5
∴ m × 5 - 6n × 5 = -7 × 5
∴ 5m - 30n = -35 … (III)
Subtracting equation (III) from equation (I)
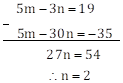
Substituting n = 2 in equation (II)
m - 6n = -7
∴ m - 6×2 = -7
∴ m - 12 = -7
∴ m = -7 + 12
∴ m = 5
∴ Solution is (m, n) = (5, 2).
Solution 2(5)
5x + 2y = -3 … (I)
x + 5y = 4 … (II)
Multiplying equation (II) by 5
∴ x × 5 + 5y × 5 = 4 × 5
∴ 5x + 25y = 20 … (III)
Subtracting equation (I) from equation (III)
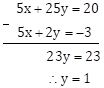
Substituting y = 1 in equation (II)
x + 5y = 4
∴ x + 5×1 = 4
∴ x + 5 = 4
∴ x = 4 - 5
∴ x = -1
∴ Solution is (x, y) = (-1, 1).
Solution 2(6)
![]()
Multiplying both sides of above equation by 3
![]()
∴ x + 3y = 10 … (I)
And,
![]()
Multiplying both sides of above equation by 4
![]()
∴ 8x + y = 11 … (II)
Multiplying equation (I) by 8
∴ x × 8 + 3y × 8 = 10 × 8
∴ 8x + 24y = 80 … (III)
Subtracting equation (II) from equation (III)
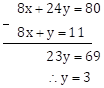
Substituting y = 3 in equation (II)
8x + y = 11
∴ 8x + 3 = 11
∴ 8x = 11 - 3
∴ 8x = 8
∴ x = 1
∴ Solution is (x, y) = (1, 3).
Solution 2(7)
99x + 101y = 499 …(I)
101x + 99y = 501 …(II)
Let's add the two equations (I) and (II)
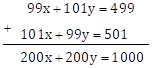
Dividing both sides of the above equation by 200
∴ x + y = 5 … (III)
Now, subtracting equation (I) from (II)
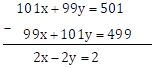
Dividing both sides of the above equation by 2
∴ x - y = 1 … (IV)
Adding the equations (III) and (IV)
∴ 2x = 6
∴ x = 3
Substituting x = 3 in equation (III)
x + y = 5
∴ 3 + y = 5
∴ y = 5 - 3
∴ y = 2
∴ Solution is (x, y) = (3, 2).
Solution 2(8)
49x - 57y = 172 … (I)
57x - 49y = 252 … (II)
Let's add the two equations (I) and (II)

Dividing both sides of the above equation by 106
∴ x - y = 4 … (III)
Now, subtracting equation (I) from (II)
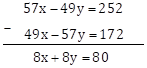
Dividing both sides of the above equation by 8
∴ x + y = 10 … (IV)
Adding the equations (III) and (IV)
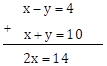
∴ x = 7
Substituting x = 7 in equation (IV)
x + y = 10
∴ 7 + y = 10
∴ y = 10 - 7
∴ y = 3
∴ Solution is (x, y) = (7, 3).
Linear Equations in Two Variables Exercise Ex. 1.2
Solution 1
(I)
x + y = 3
(II)
x - y = 4
Solution 2(1)
x + y = 6

x - y = 4

Let's plot these two equations on the graph
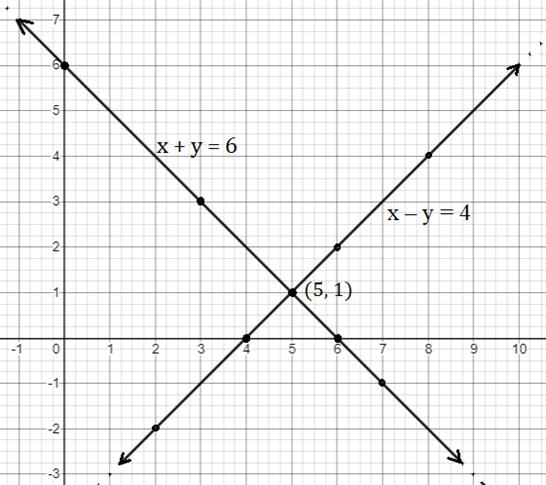
The two lines intersect at (5, 1).
So, the ordered pair i.e. x = 5, y = 1 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 5, y = 1.
Solution 2(2)
x + y = 5

x - y = 3

Let's plot these two equations on the graph
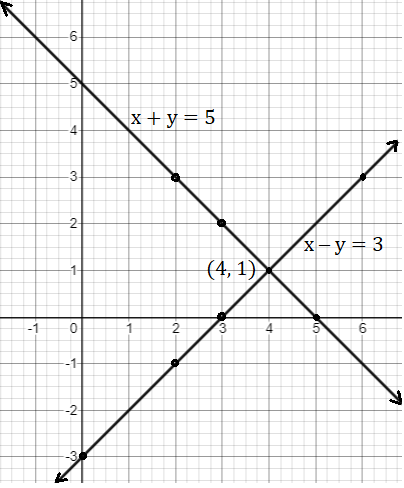
The two lines intersect at (4, 1).
So, the ordered pair i.e. x = 4, y = 1 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 4, y = 1.
Solution 2(3)
x + y = 0

2x - y = 9

Let's plot these two equations on the graph
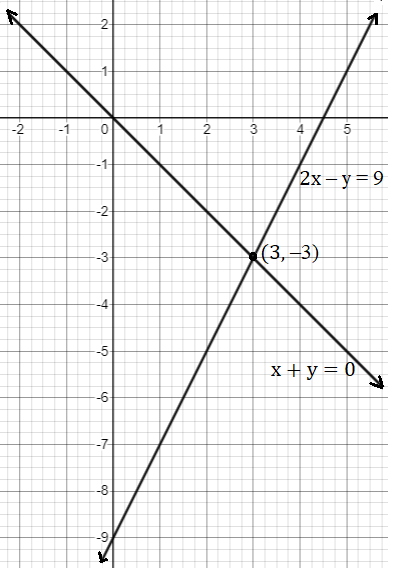
The two lines intersect at (3, -3).
So, the ordered pair i.e. x = 3, y = -3 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 3, y = -3.
Solution 2(4)
3x - y = 2

2x - y = 3

Let's plot these two equations on the graph
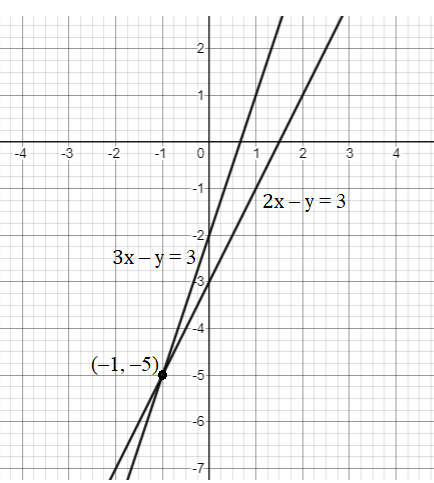
The two lines intersect at (-1, -5).
So, the ordered pair i.e. x = -1, y = -5 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = -1, y = -5.
Solution 2(5)
3x - 4y = -7
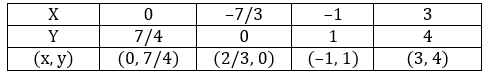
5x - 2y = 0
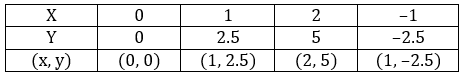
Let's plot these two equations on the graph
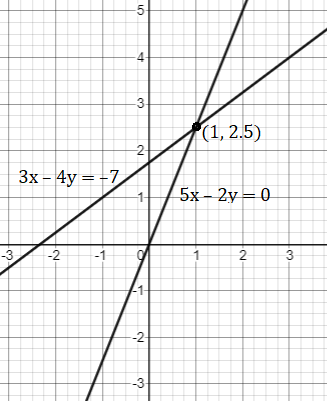
The two lines intersect at (1, 2.5).
So, the ordered pair i.e. x = 1, y = 2.5 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 1, y = 2.5.
Solution 2(6)
2x - 3y = 4
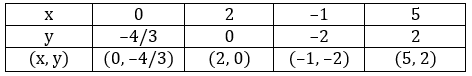
3y - x = 4

Let's plot these two equations on the graph
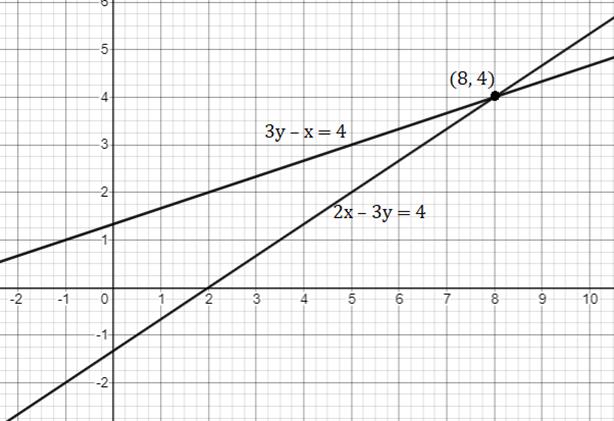
The two lines intersect at (8, 4).
So, the ordered pair i.e. x = 8, y = 4 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 8, y = 4.
Linear Equations in Two Variables Exercise Ex. 1.3
Solution 1
![]()
Solution 2(1)
![]()
Solution 2(2)
![]()
Solution 2(3)
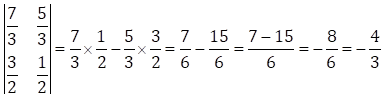
Solution 3(1)
3x - 4y = 10 … (I)
4x + 3y = 5 … (II)
![]()
![]()
![]()
![]()
![]()
∴ The solution is (x, y) = (2, -1).
Solution 3(2)
4x + 3y - 4 = 0
∴ 4x + 3y = 4 … (I)
6x = 8 - 5y
∴ 6x + 5y = 8 … (II)
![]()
![]()
![]()
![]()
![]()
∴ The solution is (x, y) = (-2, 4).
Solution 3(3)
x + 2y = -1 … (I)
2x - 3y = 12 … (II)
![]()
![]()
![]()
![]()
![]()
∴ The solution is (x, y) = (3, -2).
Solution 3(4)
6x - 4y = -12 … (I)
8x - 3y = -2 … (II)
![]()
![]()
![]()
![]()
![]()
∴ The solution is (x, y) = (2, 6).
Solution 3(5)
4m + 6n = 54 … (I)
3m + 2n = 28 … (II)
![]()
![]()
![]()
![]()
![]()
∴ The solution is (m, n) = (6, 5).
Solution 3(6)
2x + 3y = 2 … (I)
![]()
Multiplying both sides of above equation by 2.
![]()
∴ 2x - y = 1 … (II)
Let's solve the equations (I) and (II) by Cramer's rule
![]()
![]()
![]()
![]()
![]()
![]()
Linear Equations in Two Variables Exercise Ex. 1.4
Solution 1(1)
![]()
![]()
Replacing ![]() by m and
by m and ![]() by n in equations (I) and (II), we get
by n in equations (I) and (II), we get
2m - 3n = 15 … (III)
8m + 5n = 77 … (IV)
Multiplying equation (III) by 5 and equation (IV) by 3, we get
10m - 15n = 75 … (V)
24m + 15n = 231 … (VI)
Adding equations (V) and (VI)
∴ 34m = 306
∴ m = 9
Substituting m = 9 in equation (III)
∴ 2×9 - 3n = 15
∴ 18 - 3n = 15
∴ 3n = 18 - 15
∴ n = 1

![]()

![]()
∴ Solution of the given simultaneous equations is ![]()
Solution 1(2)
![]()
![]()
Replacing ![]() by
m and
by
m and ![]() by n in equations
(I) and (II), we get
by n in equations
(I) and (II), we get
10m + 2n = 4 … (III)
15m - 5n = -2 … (IV)
Multiplying equation (III) by 5 and equation (IV) by 2, we get
50m - 10n = 20 … (V)
30m - 10n = -4 … (VI)
Adding equations (V) and (VI)
∴ 80m = 16
![]()
Substituting ![]() in
equation (III)
in
equation (III)
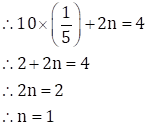
Now, ![]()
![]()
∴ x + y = 5 … (VII)
And, ![]()
![]()
∴ x - y = 1 … (VIII)
Solving equations (VII) and (VIII), we get
x = 3, y = 2
∴ Solution of the given simultaneous equations is (x,y)(3,2)
Solution 1(3)
![]()
![]()
Replacing ![]() by
m and
by
m and ![]() by n in equations
(I) and (II), we get
by n in equations
(I) and (II), we get
27m + 31n = 85 … (III)
31m + 27n = 89 … (IV)
Adding equations (III) and (IV)
∴ 58m + 58n = 174
Dividing both sides of above equation by 58, we get,
m + n = 3 … (V)
Subtracting equation (III) from equation (IV)
∴ 4m - 4n = 4
Dividing both sides of above equation by 4, we get
m - n = 1 … (VI)
Solving equations (V) and (VI)
∴ m = 2 and n = 1
Now, ![]()

And, ![]()
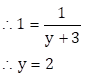
∴ Solution of the
given simultaneous equations is ![]()
Solution 1(4)
![]()
![]()
Replacing ![]() by
m and
by
m and ![]() by n in equations
(I) and (II), we get
by n in equations
(I) and (II), we get
![]()
![]()
Multiplying both sides of above equation by 2
![]()
Adding equations (III) and (V)
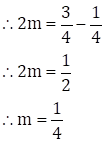
Substituting ![]() in
equation (III), we get
in
equation (III), we get
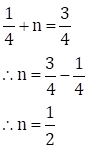
Now, ![]()
![]()
![]() … (VI)
… (VI)
And, ![]()
![]()
∴ 3x - y = 2 … (VII)
Solving equations (VI) and (VII), we get
x = 1 and y = 1
∴ Solution of the given simultaneous equations is (x, y) = (1, 1).
Linear Equations in Two Variables Exercise Ex. 1.5
Solution 1
Let the greater number be x and the smaller number be y.
From the first condition we get,
x - y = 3 … (I)
From the second condition we get,
3x + 2y = 19 … (II)
Multiplying equation (I) by 2, we get
2x - 2y = 6 … (III)
Adding equations (II) and (III), we get

∴ x = 5
Substituting x = 5 in equation (II)
3x + 2y = 19
∴ 3×5 + 2y = 19
∴ 15 + 2y = 19
∴ 2y = 4
∴ y = 2
∴ The required numbers are 5 and 2.
Solution 2
We know that, opposite sides of a rectangle are equal.
∴ 2y = x + 4
∴ x - 2y = -4 … (I)
Also, 2x + y + 8 = 4x - y
∴ 2x - 2y = 8
∴ x - y = 4… (II)
Subtracting equation (II) from equation (I), we get
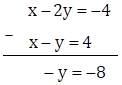
∴ y = 8
Substituting y = 8 in equation (II)
x - y = 4
∴ x - 8 = 4
∴ x = 12
Length of the rectangle = 4x - y
= 4 × 12 - 8
= 48 - 8
= 40
Breadth of the rectangle = x + 4 = 12 + 4 = 16
Perimeter of the rectangle
= 2(length + breadth)
= 2(40 + 16)
= 112 units
Area of rectangle = length × breadth = 40 × 16 = 640 sq. units
Solution 3
Let the present ages of father and son be x years and y years respectively.
From the first condition, we get
x + 2y = 70 … (I)
From the second condition, we get
2x + y = 95 … (II)
Multiplying equation (I) by 2, we get
2x + 4y = 140 … (III)
Subtracting equation (II) from (III), we get

∴ y = 15
Substituting y = 15 in equation (I)
x + 2y = 70
∴ x + 2×15 = 70
∴ x + 30 = 70
∴ x = 40
∴ The present ages of father and son are 40 years and 15 years respectively.
Solution 4
Let x and y be the numerator and the denominator of the fraction respectively.
![]()
From the first condition, we get
y = 2x + 4
∴ 2x - y = -4 … (I)
From the second condition, we get
(y - 6)= 12(x - 6)
∴ y - 6 = 12x - 72
∴ 12x - y = 72 - 6
∴ 12x - y = 66 … (II)
Subtracting equation (I) from (II), we get
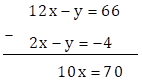
∴ x = 7
Substituting x = 7 in equation (I)
2x - y = -4
∴ 2×7 - y = -4
∴ y = 14 + 4
∴ y = 18
![]()
![]()
Solution 5
Let the weights of box of type A be x kg and that of box of type B be y kg.
Now, 1 ton = 1000 kg
∴ 10 tons = 10000 kg
From the first condition, we get
150x + 100y = 10000
Dividing both sides of the above equation by 50
∴ 3x + 2y = 200 … (I)
From the second condition, we get
260x + 40y = 10000
Dividing both sides of the above equation by 20
∴ 13x + 2y = 500 … (II)
Subtracting equation (I) from (II), we get
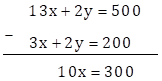
∴ x =30
Substituting x = 30 in equation (I)
3x + 2y = 200
∴ 3×30 + 2y = 200
∴ 2y = 200 - 90
∴ 2y = 110
∴ y =55
∴ Weights of box of type A is 30 kg and that of box of type B is 55 kg.
Solution 6
Let the distance Vishal travelled by bus be x km and by aeroplane be y km.
From the first condition, we get
x + y = 1900 … (I)
![]()
∴
Time required to cover x km by bus ![]()
Time required to
cover y km by aeroplane ![]()
From the second condition, we get
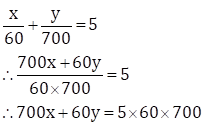
Dividing both sides of the above equation by 10
∴ 70x + 6y = 21000 … (II)
Multiplying both sides of equation (I) by 6
∴ 6x + 6y = 11400 … (III)
Subtracting equation (III) from equation (II)
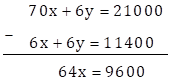
∴ x = 150
∴ The distance Vishal travelled by bus is 150 km.
Linear Equations in Two Variables Exercise Problem Set 1
Solution 1(1)
4x + 5y = 19
When x = 1
4×1 + 5y = 19
∴ 4 + 5y = 19
∴ 5y = 15
∴ y = 3
Solution 1(2)
![]()
Solution 1(3)
![]()
Solution 1(4)
x + y = 3 … (I)
3x - 2y = 4 … (II)
![]()
Solution 1(5)
Since, ![]()
![]()
∴ The given simultaneous equations have only one common solution.
Solution 2
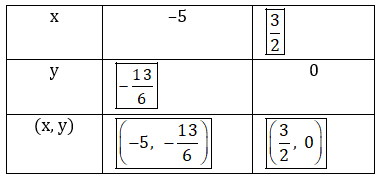
Solution 3(1)
2x + 3y = 12 …(I)
x - y = 1 …(II)
2x + 3y = 12

x - y = 1
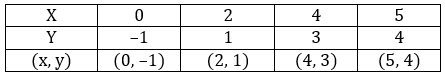
Let's plot these two equations on the graph
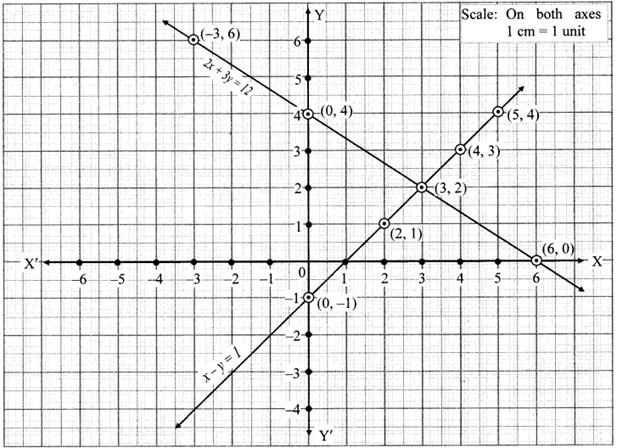
The two lines intersect at (3, 2).
So, the ordered pair i.e. x = 3, y = 2 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 3, y = 2.
Solution 3(2)
x - 3y = 1 … (I)
3x - 2y + 4 = 0
∴ 3x - 2y = -4 … (II)
x - 3y = 1
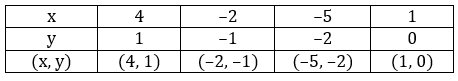
3x - 2y = -4
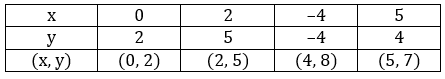
Let's plot these two equations on the graph
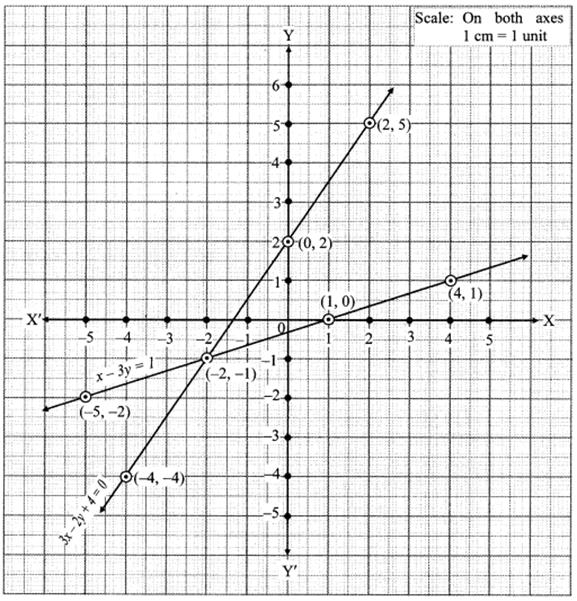
The two lines intersect at (-2, -1).
So, the ordered pair i.e. x = -2, y = -1 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = -2, y = -1.
Solution 3(3)
5x - 6y + 30 = 0
∴ 5x - 6y = -30 … (I)
5x + 4y - 20 = 0
∴ 5x + 4y = 20 … (II)
5x - 6y = -30
5x + 4y = 20

Let's plot these two equations on the graph
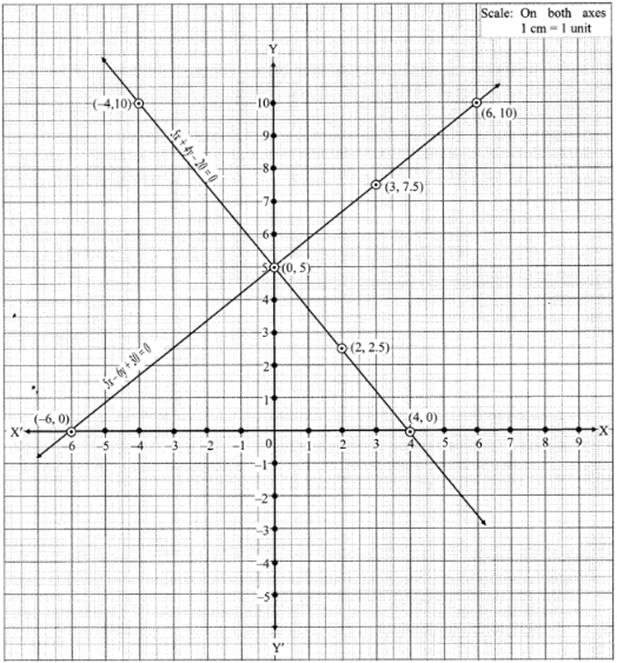
The two lines intersect at (0, 5).
So, the ordered pair i.e. x = 0, y = 5 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 0, y = 5.
Solution 3(4)
3x - y - 2 = 0
3x - y = 2 … (I)
2x + y = 8 … (II)
3x - y = 2
2x + y = 8

Let's plot these two equations on the graph
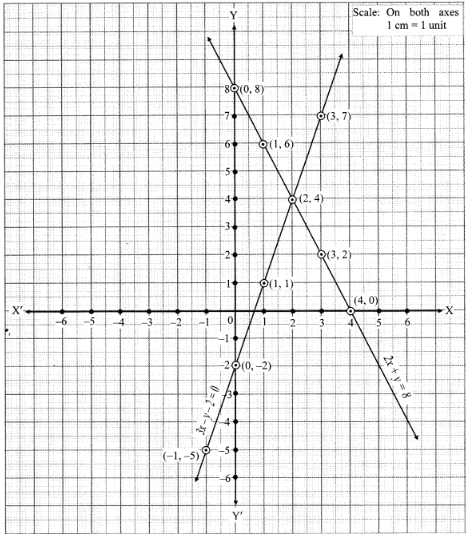
The two lines intersect at (2, 4).
So, the ordered pair i.e. x = 2, y = 4 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 2, y = 4.
Solution 3(5)
3x + y = 10 … (I)
x - y = 2 … (II)
3x + y = 10
x - y = 2

Let's plot these two equations on the graph
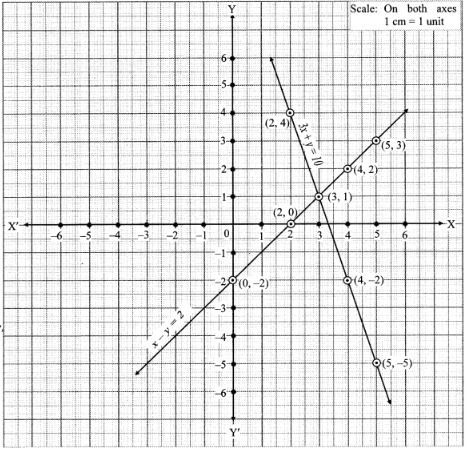
The two lines intersect at (3, 1).
So, the ordered pair i.e. x = 3, y = 1 satisfies the two equations given in (I) and (II).
∴ Solution of the given equations is x = 3, y = 1
Solution 4(1)
![]()
Solution 4(2)
![]()
Solution 4(3)
![]()
Solution 5
(1)
6x - 3y = -10 … (I)
3x + 5y - 8 = 0
∴ 3x + 5y = 8 … (II)
![]()
![]()
![]()
![]()
![]()
![]()
(2)
4m - 2n = -4 … (I)
4m + 3n = 16 … (II)
![]()
![]()
![]()
By Cramer's rule, we get
![]()
![]()
∴ The solution is (m, n) = (1, 4).
(3)
![]()
![]()
Multiplying both sides of the above equation by 3
![]() …
(II)
…
(II)
![]()
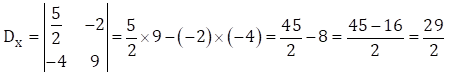

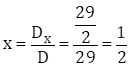
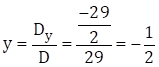
![]()
(4)
7x + 3y = 15 … (I)
12y - 5x = 39
∴ -5x + 12y = 39 … (II)
![]()
![]()
![]()
By Cramer's rule, we get
![]()
![]()
![]()
(5)
![]()
![]()
∴ 3(x + y - 8) = 2(x + 2y - 14)
∴ 3x + 3y - 24 = 2x + 4y - 28
∴ x - y = -4 … (II)
From (I), we have
![]()
∴ 4(x + y - 8) = 2(3x - y)
∴ 4x + 4y - 32 = 6x - 2y
∴ 2x - 6y = -32
∴ x - 3y = -16 … (III)
![]()
![]()
![]()
By Cramer's rule, we get
![]()
![]()
∴ The solution is (x, y) = (2, 6).
Solution 6
(1)
![]()
![]()
Replacing ![]() by m and
by m and
![]() by n in
equations (I) and (II), we get
by n in
equations (I) and (II), we get
![]()
Multiplying throughout by 3
![]()
3m + 2n = 0 … (IV)
Subtracting equation (IV) from (III)
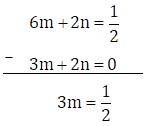
![]()
Substituting ![]() in
equation (IV), we get
in
equation (IV), we get
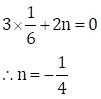
Now, ![]()
![]()
∴ x = 6
And, ![]()
![]()
∴ y = -4
∴ Solution of the given simultaneous equations is (x, y) = (6, -4).
(2)
![]() …
(I)
…
(I)
![]() …
(II)
…
(II)
Replacing ![]() by m and
by m and
![]() by n in
equations (I) and (II), we get
by n in
equations (I) and (II), we get
7m + 13n = 27 … (III)
13m + 7n = 33 … (IV)
Adding equations (III) and (IV)
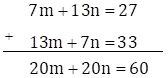
Dividing throughout by 20, we get
m + n = 3 … (V)
Subtracting equation (IV) from (III)
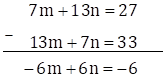
Dividing throughout by 6, we get
-m + n = -1 … (VI)
Adding equations (V) and (VI)
∴ 2n = 2
∴ n = 1
Substituting n = 1 in (V)
m + n = 3
∴ m + 1 = 3
∴ m = 2
Now, ![]()
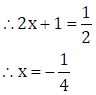
And, ![]()
![]()
∴ y = -4
∴
Solution of the given simultaneous equations is ![]() .
.
(3)
![]()
Multiplying throughout by xy, we get
148y + 231x = 527
∴ 231x + 148y = 527 … (I)
![]()
Multiplying throughout by xy, we get
231y + 148x = 610
148x + 231y = 610 … (II)
Adding equations (I) and (II)
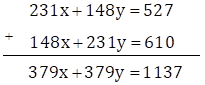
Dividing both sides of the equation by 379, we get
x + y = 3 … (III)
Subtracting equation (II) from (I)
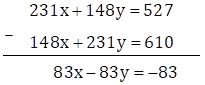
Dividing both sides of the equation by 83, we get
x - y = -1 … (IV)
Adding equations (III) and (IV)
∴ 2x = 2
∴ x = 1
Substituting x = 1 in (III)
x + y = 3
∴ 1 + y = 3
∴ y = 2
∴ Solution of the given simultaneous equations is (x, y) = (1, 2).
(4)

![]() …
(I)
…
(I)
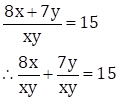
![]() …
(II)
…
(II)
Replacing ![]() by m and
by m and
![]() by n in
equations (I) and (II), we get
by n in
equations (I) and (II), we get
7n - 2m = 5
∴ -2m + 7n = 5 … (III)
7m + 8n = 15 … (IV)
Multiplying both sides of equation (III) by 7
∴ -14m + 49n = 35 … (V)
Multiplying both sides of equation (IV) by 2
∴ 14m + 16n = 30 … (VI)
Adding equations (V) and (VI)
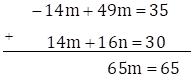
∴ m = 1
Substituting m = 1 in equation (IV)
7m + 8n = 15
∴ 7×1 + 8n = 15
∴ 8n = 8
∴ n = 1
Now, ![]()
∴ x = 1
And, ![]()
∴ y = 1
∴ Solution of the given simultaneous equations is(x, y) = (1, 1).
(5)
![]() …
(I)
…
(I)
![]() …
(II)
…
(II)
Replacing ![]() by m and
by m and
![]() by n in
equations (I) and (II), we get
by n in
equations (I) and (II), we get
![]()
Multiplying both sides of the equation by 20
∴ 10m + 4n = 5 … (III)
Also, ![]()
Multiplying both sides of the above equation by 2
∴ 10m - 4n = -3 … (IV)
Adding equations (III) and (IV)
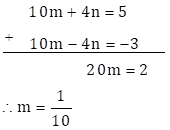
Substituting ![]() in
equation (III)
in
equation (III)
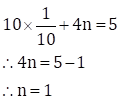
Now, ![]()
![]()
∴ 3x + 4y = 10 … (V)
And, ![]()
![]()
∴ 2x - 3y = 1 … (VI)
Multiplying equation (V) by 3 and equation (VI) by 4
9x + 12y = 30 … (VII)
8x - 12y = 4 … (VIII)
Adding equations (VII) and (VIII)
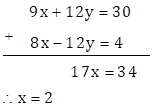
Substituting x = 2 in the equation (V)
3x + 4y = 10
∴ 3×2 + 4y = 10
∴ 4y = 10 - 6
∴ y = 1
∴ Solution of the given simultaneous equations is (x, y) = (2, 1).
Solution 7(1)
Let the digit in unit's place is x and that in the ten's place is y.
∴ the number = 10y + x
The number obtained
by interchanging the digits is ![]() .
.
According to first condition,
Two digit number + the number obtained by interchanging the digits = 143
∴
10y + x + ![]() = 143
= 143
∴
![]() = 143
= 143
Dividing both the sides by 11
∴
x + y = ![]() … (I)
… (I)
From the second condition,
digit in unit's place = digit in the ten's place + 3
x = ![]() +
3
+
3
∴ x - y = 3 … (II)
Adding equations (I) and (II)
2x = ![]()
∴ x = 8
Putting this value of x in equation (I)
x + y = 13
∴
8 + ![]() = 13
= 13
∴
y = ![]()
The original number is (10y + x)
= ![]() + 8
+ 8
= 58
Solution 7(2)
Let the rate of tea be Rs x per kg and that of sugar be Rs y per kg.
From the first condition, we have
Cost of 1½ kg tea + Cost of 5 kg sugar + fare for rickshaw = Total expense
∴ 1½ x + 5y + 50 = 700
∴ 3/2 x + 5y = 650
∴ 3x + 10y = 1300 … (I)
From the second condition, we have
Cost of 2 kg tea Cost of 7 kg sugar = Total expense
∴ 2x + 7y = 880 … (II)
Multiplying equation (I) by 2
∴ 6x + 20y = 2600 … (III)
Multiplying equation (II) by 3
∴ 6x + 21y = 2640 … (IV)
Subtracting equation (III) from (IV)
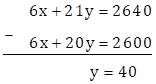
Substituting y = 40 in equation (I)
3x + 10y = 1300
∴ 3x + 10×40 = 1300
∴ 3x = 1300 - 400
∴ 3x = 900
∴ x = 300
∴ The rate of tea is Rs 300 per kg and that of sugar is Rs. 40 per kg.
Solution 7(3)
Anushka had x notes of Rs 100 and y notes of Rs 50.
From the first condition,
100x + 50y = 2500
Dividing both sides of the equation by 50
∴ 2x + y = 50 … (I)
From the second condition,
100y + 50x = 2000
Dividing both sides of the equation by 50
∴ 2y + x = 40
∴ x + 2y = 40 … (II)
Multiplying both sides of equation (II) by 2
∴ 2x + 4y = 80 … (III)
Subtracting equation (I) from (III), we get
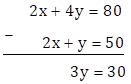
∴ y = 10
Substituting y = 10 in equation (I)
2x + y = 50
∴ 2x + 10 = 50
∴ 2x = 40
∴ x = 20
∴ Anushka had 20 notes of Rs 100 and 10 notes of Rs 50.
Solution 7(4)
Let the present ages of Manish and Savita be x years and y years respectively.
From the first condition,
x + y = 31 … (I)
3 years ago,
Manish's age = (x - 3) years
Savita's age = (y - 3) years
From the second condition,
(x - 3) = 4 (y - 3)
∴ x - 3 = 4y - 12
∴ x - 4y = -12 + 3
∴ x - 4y = -9 … (II)
Subtracting equation (II) from (I), we get

∴ y = 8
Substituting y = 8 in equation (I), we get
x + 8 = 31
∴ x = 23
∴ The present ages of Manish and Savita are 23 years and 8 years respectively.
Solution 7(5)
Let the daily wages of skilled workers be Rs x and that of unskilled workers be Rs y.
From the first condition,
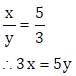
∴ 3x - 5y = 0 … (I)
From the second condition,
x + y = 720 … (II)
Multiplying equation (II) by 5
∴ 5x + 5y = 3600 … (III)
Adding equations (I) and (III)
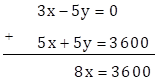
∴ x = 450
Substituting x = 450 in equation (I)
∴ 3×450 - 5y = 0
∴ 5y = 1350
∴ y = 270
∴ The daily wages of skilled workers is Rs 450 and that of unskilled workers is Rs 270.
Solution 7(6)
Let the speeds of Hamid and Joseph be x km/hr andy km/hr respectively.
Distance travelled
by Hamid in 20 minutes i.e. ![]() hrs
hrs ![]() x km
x km
Distance travelled
by Joseph in 20 minutes i.e. ![]() hrs
hrs ![]() y km
y km
From the first condition, we get
![]()
Multiplying both sides of the equation by 30
∴ x + y = 90 … (I)
From the second condition, we have
3x - 3y = 30
Dividing both sides of the equation by 3
∴x - y = 10 … (II)
Adding equations (I) and (II), we get
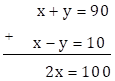
∴ x = 50
Substituting x = 50 in equation (I), we get
50 + y = 90
∴ y = 90 - 50
∴ y = 40
∴ The speeds of Hamid and Joseph are 50 km/hr and 40 km/hr respectively.

