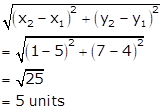Class 10 SELINA Solutions Maths Chapter 13 - Section and Mid-Point Formula
Section and Mid-Point Formula Exercise Ex. 13(A)
Solution 2
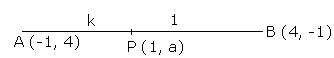
Let the point P (1, a) divides the line segment AB in the ratio k: 1.
Using section formula, we have:

Solution 3
Let the point P (a, 6) divides the line segment joining A (-4, 3) and B (2, 8) in the ratio k: 1.
Using section formula, we have:

Solution 4
Let the point P (x, 0) on x-axis divides the line segment joining A (4, 3) and B (2, -6) in the ratio k: 1.
Using section formula, we have:
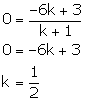
Thus, the required ratio is 1: 2.
Also, we have:
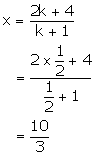
Thus, the required co-ordinates of the point of intersection are ![]() .
.
Solution 5
![]()
Let S (0, y) be the point on y-axis which divides the line segment PQ in the ratio k: 1.
Using section formula, we have:
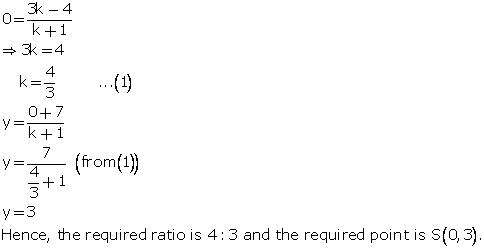
Solution 6

Point A divides PO in the ratio 1: 4.
Co-ordinates of point A are:
![]()
Point B divides PO in the ratio 2: 3.
Co-ordinates of point B are:
![]()
Point C divides PO in the ratio 3: 2.
Co-ordinates of point C are:
![]()
Point D divides PO in the ratio 4: 1.
Co-ordinates of point D are:
![]()
Solution 7
Let the co-ordinates of point P are (x, y).
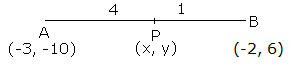
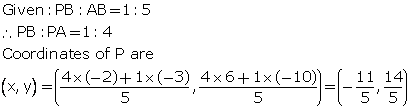
Solution 8
5AP = 2BP
![]()
The co-ordinates of the point P are
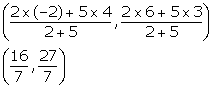
Solution 9
The co-ordinates of every point on the line x = 2 will be of the type (2, y).
Using section formula, we have:
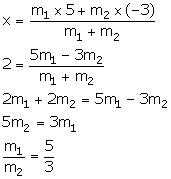
Thus, the required ratio is 5: 3.
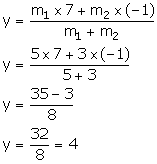
Thus, the required co-ordinates of the point of intersection are (2, 4).
Solution 10
The co-ordinates of every point on the line y = 2 will be of the type (x, 2).
Using section formula, we have:
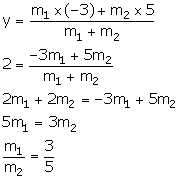
Thus, the required ratio is 3: 5.
Solution 11
Point A lies on x-axis. So, let the co-ordinates of A be (x, 0).
Point B lies on y-axis. So, let the co-ordinates of B be (0, y).
P divides AB in the ratio 2: 5.
We have:
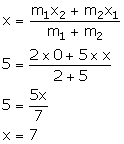
Thus, the co-ordinates of point A are (7, 0).
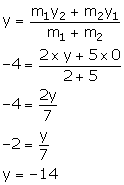
Thus, the co-ordinates of point B are (0, -14).
Solution 12
Let P and Q be the points of trisection of the line segment joining the points A(-3, 0) and B(6, 6).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are

We have AQ: QB = 2: 1
Co-ordinates of the point Q are

Solution 13
Let P and Q be the points of trisection of the line segment joining the points A (-5, 8) and B (10, -4).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are
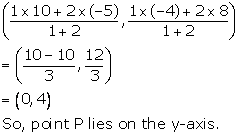
We have AQ: QB = 2: 1
Co-ordinates of the point Q are
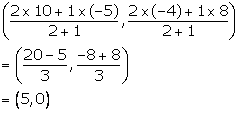
So, point Q lies on the x-axis.
Hence, the line segment joining the given points A and B is trisected by the co-ordinate axes.
Solution 14
Let A and B be the point of trisection of the line segment joining the points P (2, 1) and Q (5, -8).
So, PA = AB = BQ
We have PA: AQ = 1: 2
Co-ordinates of the point A are
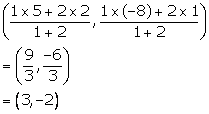
Hence, A (3, -2) is a point of trisection of PQ.
We have PB: BQ = 2: 1
Co-ordinates of the point B are

Solution 15
Since, point L lies on y-axis, its abscissa is 0.
Let the co-ordinates of point L be (0, y). Let L divides MN in the ratio k: 1.
Using section formula, we have:
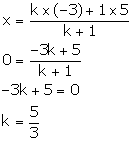
Thus, the required ratio is 5: 3.
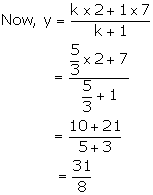
Solution 16
BP: PC = 2: 3
Co-ordinates of P are
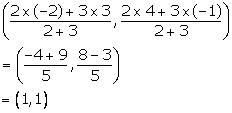
Using distance formula, we have:
![]()
Solution 17
Since, point K lies on x-axis, its ordinate is 0.
Let the point K (x, 0) divides AB in the ratio k: 1.
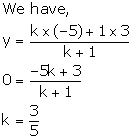
Thus, K divides AB in the ratio 3: 5.
Also, we have:
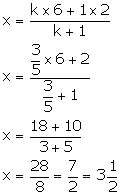
Thus, the co-ordinates of the point K are ![]() .
.
Solution 18
Since, point K lies on y-axis, its abscissa is 0.
Let the point K (0, y) divides AB in the ratio k: 1.
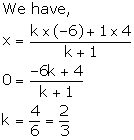
Thus, K divides AB in the ratio 2: 3.
Also, we have:
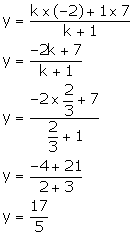
Thus, the co-ordinates of the point K are ![]() .
.
Solution 19
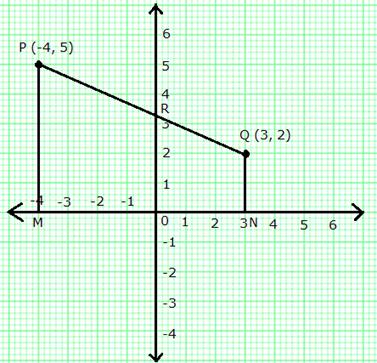
(i) Let point R (0, y) divides PQ in the ratio k: 1.
We have:
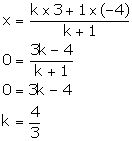
Thus, PR: RQ = 4: 3
(ii) Also, we have:
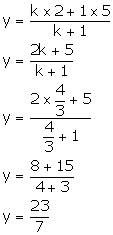
Thus, the co-ordinates of point R are ![]() .
.
(iii) Area of quadrilateral PMNQ
= ![]() (PM + QN)
(PM + QN) ![]() MN
MN
= ![]() (5 + 2)
(5 + 2) ![]() 7
7
= ![]() 7
7 ![]() 7
7
= 24.5 sq units
Solution 20
Given, A lies on x-axis and B lies on y-axis.
Let the co-ordinates of A and B be (x, 0) and (0, y) respectively.
Given, P is the point (-4, 2) and AP: PB = 1: 2.
Using section formula, we have:
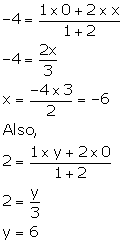
Thus, the co-ordinates of points A and B are (-6, 0) and (0, 6) respectively.
Solution 21
(i)

(ii)
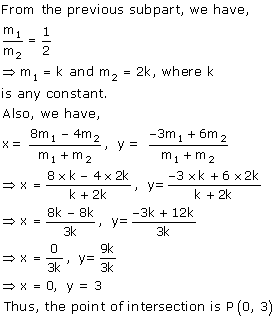
(iii)

Solution 22
Take (x1 , y1) = (-3, 3a + 1) ; (x2 , y2) = (5, 8a) and
(x, y) = (-b, 9a - 2)
Here m1 = 3 and m2 =1
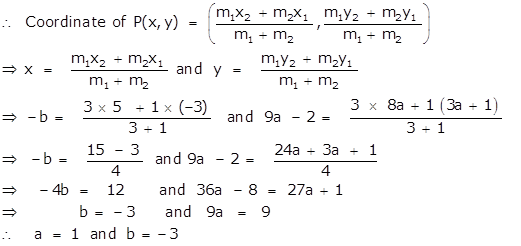
Section and Mid-Point Formula Exercise Ex. 13(B)
Solution 2
Mid-point of AB = (2, 3)
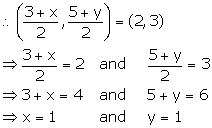
Solution 3
(i) Let the co-ordinates of A be (x, y).
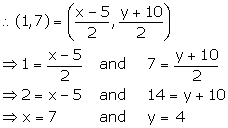
Hence, the co-ordinates of A are (7, 4).
(ii) Let the co-ordinates of B be (x, y).
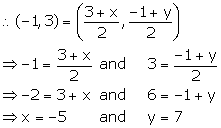
Hence, the co-ordinates of B are (-5, 7).
Solution 4
Point A lies on y-axis, so let its co-ordinates be (0, y).
Point B lies on x-axis, so let its co-ordinates be (x, 0).
P (-3, 2) is the mid-point of line segment AB.
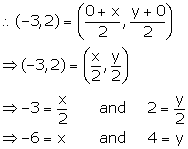
Thus, the co-ordinates of points A and B are (0, 4) and (-6, 0) respectively.
Solution 5
Let A (-5, 2), B (3, -6) and C (7, 4) be the vertices of the given triangle.
Let AD be the median through A, BE be the median through B and CF be the median through C.
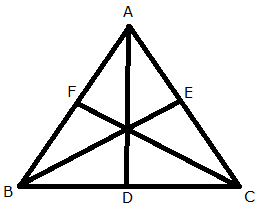
We know that median of a triangle bisects the opposite side.
Co-ordinates of point F are
![]()
Co-ordinates of point D are
![]()
Co-ordinates of point E are
![]()
The median of the triangle through the vertex B(3, -6) is BE
Using distance formula,
![]()
Solution 6
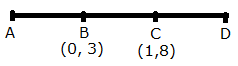
Given, AB = BC = CD
So, B is the mid-point of AC. Let the co-ordinates of point A be (x, y).
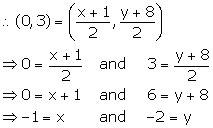
Thus, the co-ordinates of point A are (-1, -2).
Also, C is the mid-point of BD. Let the co-ordinates of point D be (p, q).
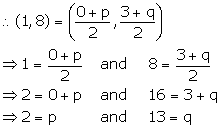
Thus, the co-ordinates of point D are (2, 13).
Solution 7
Co-ordinates of the mid-point of AC are
![]()
Co-ordinates of the mid-point of BD are
![]()
Since, mid-point of AC = mid-point of BD
Hence, ABCD is a parallelogram.
Solution 8
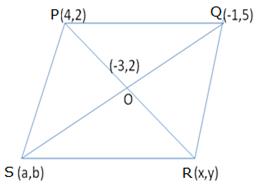
Let the coordinates of R and S be (x,y) and (a,b) respectively.
Mid-point of PR is O.
![]() O(-3,2) =
O(-3,2) = ![]()
![]()
-6 = 4 + x, 4 = 2 + y
x = -10 , y = 2
Hence, R = (-10,2)
Similarly, the mid-point of SQ is O.
![]()
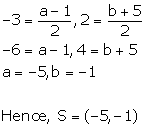
Thus, the coordinates of the point R and S are (-10, 2) and (-5, -1).
Solution 9
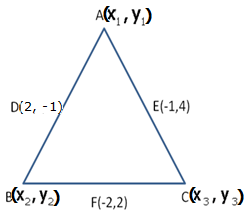
Let A(x1,y1), B![]() and C
and C![]() be the co-ordinates of the vertices of
be the co-ordinates of the vertices of ![]() ABC.
ABC.
Midpoint of AB, i.e. D
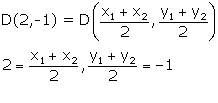
![]()
![]()
Similarly,
![]()
![]()
![]()
![]()
Adding (1), (3) and (5), we get,
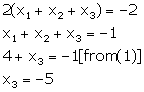
From (3)
![]()
From (5)
![]()
Adding (2), (4) and (6), we get,
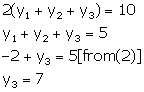
From (4)
![]()
From (6)
![]()
Thus, the co-ordinates of the vertices of ![]() ABC are (3, 1), (1, -3) and (-5, 7).
ABC are (3, 1), (1, -3) and (-5, 7).
Solution 10
Given, AB = BC, i.e., B is the mid-point of AC.

Solution 11
Given, PR = 2QR
Now, Q lies between P and R, so, PR = PQ + QR
![]() PQ + QR = 2QR
PQ + QR = 2QR
![]() PQ = QR
PQ = QR
![]() Q is the mid-point of PR.
Q is the mid-point of PR.
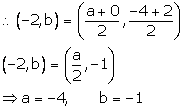
Solution 12
Let G be the centroid of DPQR whose coordinates are (2, -5) and let (x,y) be the coordinates of vertex P.
Coordinates of G are,
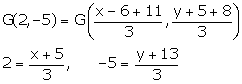
6 = x + 5, -15 = y + 13
x = 1, y = -28
Coordinates of vertex P are (1, -28)
Solution 13
Given, centroid of triangle ABC is the origin.
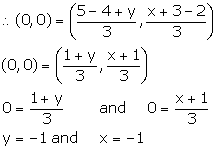
Section and Mid-Point Formula Exercise TEST YOURSELF
Solution 2
Given, BP: PC = 3: 2
Using section formula, the co-ordinates of point P are

Using distance formula, we have:
![]()
Solution 3
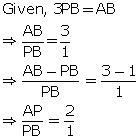
Using section formula,
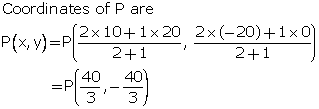
Given, AB = 6AQ
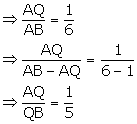
Using section formula,
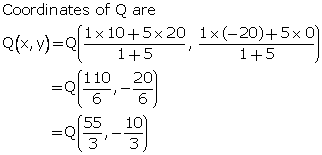
Solution 4
Given that, point P lies on AB such that AP: PB = 3: 5.
The co-ordinates of point P are

Also, given that, point Q lies on AC such that AQ: QC = 3: 5.
The co-ordinates of point Q are

Using distance formula,
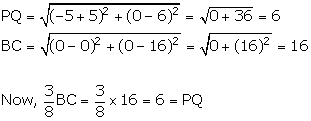
Hence, proved.
Solution 5
Since, the line segment AB intersects the y-axis at point P, let the co-ordinates of point P be (0, y).
P divides AB in the ratio 1: 3.

Thus, the value of a is 3 and the co-ordinates of point P are![]() .
.
Solution 6
Let the line segment AB intersects the x-axis at point P (x, 0) in the ratio k: 1.
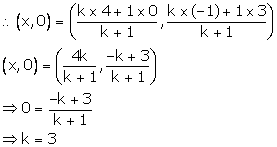
Thus, the required ratio in which P divides AB is 3: 1.
Also, we have:
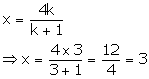
Thus, the co-ordinates of point P are (3, 0).
Solution 7
Since, point A lies on x-axis, let the co-ordinates of point A be (x, 0).
Since, point B lies on y-axis, let the co-ordinates of point B be (0, y).
Given, mid-point of AB is C (4, -3).
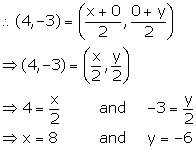
Thus, the co-ordinates of point A are (8, 0) and the co-ordinates of point B are (0, -6).
Solution 8
![]()

Solution 9
It is given that the mid-point of the line-segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a).
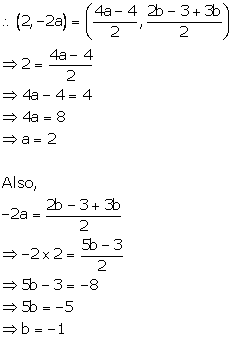
Solution 10
(i) Co-ordinates of point P are

(ii) OP = ![]()
(iii) Let AB be divided by the point P (0, y) lying on y-axis in the ratio k: 1.

Thus, the ratio in which the y-axis divide the line AB is 4: 17.
Solution 11
We have:
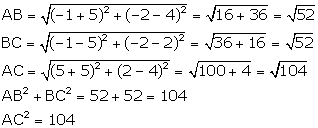
![]() AB = BC and
AB = BC and ![]()
![]() ABC is an isosceles right-angled triangle.
ABC is an isosceles right-angled triangle.
Let the coordinates of D be (x, y).
If ABCD is a square, then,
Mid-point of AC = Mid-point of BD
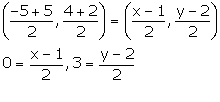
x = 1, y = 8
Thus, the co-ordinates of point D are (1, 8).
Solution 12
Given, M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1).
The co-ordinates of point M are

Also, given that, R (2, 2) divides the line segment joining M and the origin in the ratio p: q.

Thus, the ratio p: q is 1: 2.
Solution 13

Solution 14

Solution 15
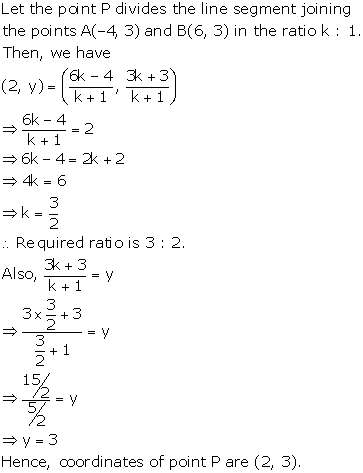
Solution 16
Let A' = (x, y) be the image of the point A(5, -3), under reflection in the point P(-1, 3).
⇒ P(-1, 3) is the mid - point of the line segment AA'.
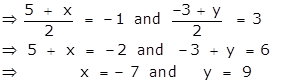
Therefore the image of the point A(5, -3), under reflection in the point P(-1, 3) is A'(-7, 9).
Solution 17

Solution 18
Centroid of a △ABC =![]() …… (i)
…… (i)
G(3, 4) is a centroid of △ABC ….. given
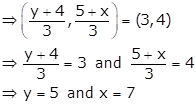
Therefore, the coordinates of B and C are (5, 4) and (1, 7) respectively.
Length of the side BC