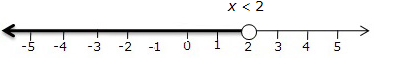Class 10 SELINA Solutions Maths Chapter 4 - Linear Inequations (in one variable)
Linear Inequations (in one variable) Exercise Ex. 4(A)
Solution 1(a)
Correct Option: (i) {–8, –6, –5, –4, 6}
The elements in the set {–8, –6, –5, –4, 6} do not satisfy the replacement set.
Solution 1(b)
Correct Option: (ii) x < 8
4(2x – 5) < 2x + 28
8x – 20 < 2x + 28
8x – 2x < 28 + 20
6x < 48
x < 8
Solution 1(c)
Correct Option: (iv) {x : x ∊ R, x ≥ 2}
–2x + 7 ≤ 3
–2x ≤ 3 – 7
–2x ≤ –4
–x ≤ –2
x ≥ 2
Therefore, the solution set is {x : x ∊ R, x ≥ 2}.
Solution 1(d)
Correct Option: (i) x > 3
7 – 3x < x – 5
7 + 5 < x + 3x
12 < 4x
3 < x
i.e. x > 3
Solution 1(e)
Correct Option: (iii) 0 < x < 8
x(8 – x) > 0
8 – x > 0
8 > x
Since x ∊ N, 0 < x < 8.
Solution 2

Solution 3
(i) a < b ![]() a - c < b - c
a - c < b - c
The given statement is true.
(ii) If a > b ![]() a + c > b + c
a + c > b + c
The given statement is true.
(iii) If a < b ![]() ac < bc
ac < bc
The given statement is false.
(iv) If a > b ![]()
![]()
The given statement is false.
(v) If a - c > b - d ![]() a + d > b + c
a + d > b + c
The given statement is true.
(vi) If a < b ![]() a - c < b - c (Since, c > 0)
a - c < b - c (Since, c > 0)
The given statement is false.
Solution 4
(i) 5x + 3 ![]() 2x + 18
2x + 18
5x - 2x ![]() 18 - 3
18 - 3
3x ![]() 15
15
x ![]() 5
5
Since, x ![]() N, therefore solution set is {1, 2, 3, 4, 5}.
N, therefore solution set is {1, 2, 3, 4, 5}.
(ii) 3x - 2 < 19 - 4x
3x + 4x < 19 + 2
7x < 21
x < 3
Since, x ![]() N, therefore solution set is {1, 2}.
N, therefore solution set is {1, 2}.
Solution 5
(i) x + 7 ![]() 11
11
x ![]() 11 - 7
11 - 7
x ![]() 4
4
Since, the replacement set = W (set of whole numbers)
![]() Solution set = {0, 1, 2, 3, 4}
Solution set = {0, 1, 2, 3, 4}
(ii) 3x - 1 > 8
3x > 8 + 1
x > 3
Since, the replacement set = W (set of whole numbers)
![]() Solution set = {4, 5, 6, …}
Solution set = {4, 5, 6, …}
(iii) 8 - x > 5
- x > 5 - 8
- x > -3
x < 3
Since, the replacement set = W (set of whole numbers)
![]() Solution set = {0, 1, 2}
Solution set = {0, 1, 2}
(iv) 7 - 3x ![]()
![]()
-3x ![]()
![]() - 7
- 7
-3x ![]()
![]()
x ![]()
![]()
Since, the replacement set = W (set of whole numbers)
![]() Solution set = {0, 1, 2}
Solution set = {0, 1, 2}
Solution 6
3 - 2x ![]() x - 12
x - 12
-2x - x ![]() -12 - 3
-12 - 3
-3x ![]() -15
-15
x ![]() 5
5
Since, x ![]() N, therefore,
N, therefore,
Solution set = {1, 2, 3, 4, 5}
Solution 7
25 - 4x ![]() 16
16
-4x ![]() 16 - 25
16 - 25
-4x ![]() -9
-9
x ![]()
x ![]()
(i) The smallest value of x, when x is a real number, is 2.25.
(ii) The smallest value of x, when x is an integer, is 3.
Solution 8
![]()
Since, the replacement set of real numbers.
![]() Solution set = {x: x
Solution set = {x: x ![]() R and
R and ![]() }
}
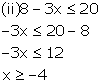
Since, the replacement set of real numbers.
![]() Solution set = { x: x
Solution set = { x: x ![]() R and
R and ![]() }
}
Solution 9

Thus, the required smallest value of x is -1.
Solution 10
2(x - 1) ![]() 9 - x
9 - x
2x - 2 ![]() 9 - x
9 - x
2x + x ![]() 9 + 2
9 + 2
3x ![]() 11
11
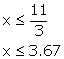
Since, x ![]() W, thus the required largest value of x is 3.
W, thus the required largest value of x is 3.
Linear Inequations (in one variable) Exercise Ex. 4(B)
Solution 1(a)
Correct Option: (iii) {x : x ∊ R and –2 < x ≤ 4}
The solution set is {x : x ∊ R and –2 < x ≤ 4}.
Solution 1(b)
Correct Option: (ii) {x : x ∊ Z and –3 ≤ x}
The solution set is {x : x ∊ Z and –3 ≤ x}.
Solution 1(c)
Correct Option: (ii) {(x < 10) ⋃ (x > 10)}
The solution set is {(x < 10) ⋃ (x > 10)}.
Solution 1(d)
Correct Option: (iv) {x : x ∊ R, x ≤ –2 or x ≥ 3}
The solution set is {x : x ∊ R, x ≤ –2 or x ≥ 3}.
Solution 1(e)
Correct Option: (ii)
![]()
The required number line is
![]()
Solution 2
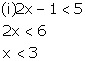
Solution on number line is:
![]()

Solution on number line is:

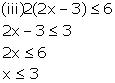
Solution on number line is:
![]()
![]()
Solution on number line is:
![]()
![]()
Solution on number line is:
![]()
![]()
Solution on number line is:
![]()
![]()
Solution on number line is:
![]()
Solution 3
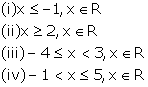
Solution 4
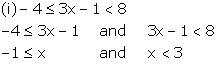
The solution set on the real number line is:
![]()
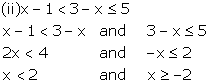
The solution set on the real number line is:
![]()
Solution 5
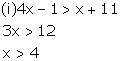
The solution on number line is as follows:

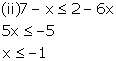
The solution on number line is as follows:
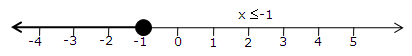
![]()
The solution on number line is as follows:
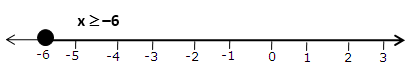
(iv) 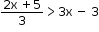
2x + 5 > 9x -3
-7x > -14
x < 2
The solution on number line is:
Solution 6
-1 < 3 - 2x ![]() 7
7
-1 < 3 - 2x and 3 - 2x ![]() 7
7
2x < 4 and -2x ![]() 4
4
x < 2 and x ![]() -2
-2
Solution set = {-2 ![]() x < 2, x
x < 2, x ![]() R}
R}
Thus, the solution can be represented on a number line as:
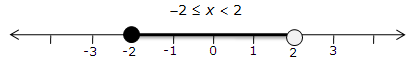
Solution 7
-3 < x - 2 ![]() 9 - 2x
9 - 2x
-3 < x - 2 and x - 2 ![]() 9 - 2x
9 - 2x
-1 < x and 3x ![]() 11
11
-1 < x ![]()
![]()
Since, x ![]() N
N
![]() Solution set = {1, 2, 3}
Solution set = {1, 2, 3}
Solution 8
![]()
![]()
![]()
![]()
![]() -3
-3 ![]() x and x < 3
x and x < 3
![]() -3
-3 ![]() x < 3
x < 3
The required graph of the solution set is:
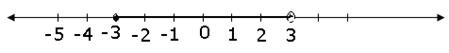
Solution 9

Thus, the solution set is {x ∊ N: -2 ≤ x ≤3.75}
Since x ∊ N, the values of x are 1, 2, 3
The solution on number line is given by
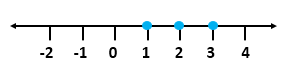
Solution 10
-5 ![]() 2x - 3 < x + 2
2x - 3 < x + 2
-5 ![]() 2x - 3 and 2x - 3 < x + 2
2x - 3 and 2x - 3 < x + 2
-2 ![]() 2x and x < 5
2x and x < 5
-1 ![]() x and x < 5
x and x < 5
![]() Required range is -1
Required range is -1 ![]() x < 5.
x < 5.
The required graph is:

Solution 11
5x - 3 ![]() 5 + 3x
5 + 3x ![]() 4x + 2
4x + 2
5x - 3 ![]() 5 + 3x and 5 + 3x
5 + 3x and 5 + 3x ![]() 4x + 2
4x + 2
2x ![]() 8 and -x
8 and -x ![]() -3
-3
x ![]() 4 and x
4 and x ![]() 3
3
Thus, 3 ![]() x
x ![]() 4.
4.
Hence, a = 3 and b = 4.
Solution 12
2x - 3 < x + 2 ![]() 3x + 5
3x + 5
2x - 3 < x + 2 and x + 2 ![]() 3x + 5
3x + 5
x < 5 and -3 ![]() 2x
2x
x < 5 and -1.5 ![]() x
x
Solution set = {-1.5 ![]() x < 5}
x < 5}
The solution set can be graphed on the number line as:
![]()
Solution 13
(i) 2x - 9 < 7 and 3x + 9 ![]() 25
25
2x < 16 and 3x ![]() 16
16
x < 8 and x ![]() 5
5![]()
![]() Solution set = { x
Solution set = { x ![]() 5
5![]() , x
, x ![]() R}
R}
The required graph on number line is:

(ii) 2x - 9 ![]() 7 and 3x + 9 > 25
7 and 3x + 9 > 25
2x ![]() 16 and 3x > 16
16 and 3x > 16
x ![]() 8 and x > 5
8 and x > 5![]()
![]() Solution set = {5
Solution set = {5![]() < x
< x ![]() 8, x
8, x ![]() I} = {6, 7, 8}
I} = {6, 7, 8}
The required graph on number line is:
![]()
(iii) x + 5 ![]() 4(x - 1) and 3 - 2x < -7
4(x - 1) and 3 - 2x < -7
9 ![]() 3x and -2x < -10
3x and -2x < -10
3 ![]() x and x > 5
x and x > 5
![]() Solution set = Empty set
Solution set = Empty set
Solution 14
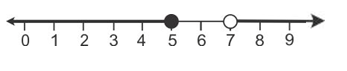
3x - 2 > 19 or 3 - 2x ![]() -7
-7
3x > 21 or -2x ![]() -10
-10
x > 7 or x ![]() 5
5
Graph of solution set of x > 7 or x ![]() 5 = Graph of points which belong to x > 7 or x
5 = Graph of points which belong to x > 7 or x ![]() 5 or both.
5 or both.
Thus, the graph of the solution set is:
Solution 15
(i) A = {x ![]() R: -2
R: -2 ![]() x < 5}
x < 5}
B = {x ![]() R: -4
R: -4 ![]() x < 3}
x < 3}
(ii) A ![]() B = {x
B = {x ![]() R: -2
R: -2 ![]() x < 5}
x < 5}
It can be represented on number line as:
![]()
B' = {x ![]() R: 3 < x
R: 3 < x ![]() -4}
-4}
A ![]() B' = {x
B' = {x ![]() R: 3
R: 3 ![]() x < 5}
x < 5}
It can be represented on number line as:

Solution 16
(i) A ![]() B = {x: -1 < x < 3, x
B = {x: -1 < x < 3, x ![]() R}
R}
It can be represented on a number line as:
![]()
(ii) Numbers which belong to B but do not belong to A' = B - A
A' ![]() B = {x: -4
B = {x: -4 ![]() x
x ![]() -1, x
-1, x ![]() R}
R}
It can be represented on a number line as:
![]()
(iii) A - B = {x: 3 ![]() x
x ![]() 5, x
5, x ![]() R}
R}
It can be represented on a number line as:
![]()
Solution 17
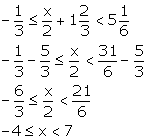
(i)If x ![]() W, range of values of x is {0, 1, 2, 3, 4, 5, 6}.
W, range of values of x is {0, 1, 2, 3, 4, 5, 6}.
![]()
(ii) If x ![]() Z, range of values of x is {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}.
Z, range of values of x is {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}.
![]()
(iii)If x ![]() R, range of values of x is
R, range of values of x is ![]() .
.
![]()
Solution 18
A = {x: -8 < 5x + 2 ![]() 17, x
17, x ![]() I}
I}
= {x: -10 < 5x ![]() 15, x
15, x ![]() I}
I}
= {x: -2 < x ![]() 3, x
3, x ![]() I}
I}
It can be represented on number line as follows:
![]()
B = {x: -2 ![]() 7 + 3x < 17, x
7 + 3x < 17, x ![]() R}
R}
= {x: -9 ![]() 3x < 10, x
3x < 10, x ![]() R}
R}
= {x: -3 ![]() x < 3.33, x
x < 3.33, x ![]() R}
R}
It can be represented on number line as follows:

A ![]() B = {-1, 0, 1, 2, 3}
B = {-1, 0, 1, 2, 3}
Solution 19
2x - 5 ≤ 5x + 4 and 5x +4 < 11
2x - 9 ≤ 5x and 5x < 11 - 4
-9 ≤ 3x and 5x < 7
x ![]() - 3 and x <
- 3 and x < ![]()
x ![]() - 3 and x <
- 3 and x < ![]()
Since x![]() I, the solution set is
I, the solution set is ![]()
And the number line representation is
![]()
Solution 20
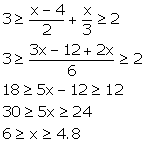
Solution set = {5, 6}
It can be graphed on number line as:
![]()
Linear Inequations (in one variable) Exercise TEST YOURSELF
Solution 1(a)
Correct Option: (ii) 4
4x ≤ 12 + x
4x – x ≤ 12
3x ≤ 12
x ≤ 4
Solution 1(b)
Correct Option: (i) 2
5x – 4 ≥ 18 – 6x
5x + 6x ≥ 18 + 4
11x ≥ 22
x ≥ 2
Solution 1(c)
Correct Option: (i) x > 1
3x + 15 < 5x + 13
15 – 13 < 5x – 3x
2 < 2x
1 < x
i.e., x > 1
Solution 1(d)
Correct Option: (i)
![]()
The solution for a number line A is –3 < x ≤ 1.
And, for a number line B, the solution is –4 ≤ x < 0.
Then, A ⋂ B = –3 < x < 0.
Hence, the required number line is
![]()
Solution 1(e)
Correct Option: (i)
![]()
The solution for a number line A is –3 < x ≤ 1.
And, for a number line B, the solution is –4 ≤ x < 0.
Then, A ⋃ B = –4 ≤ x ≤ 1.
Hence, the required number line is
![]()
Solution 2
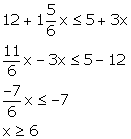
![]() Solution set = {x: x
Solution set = {x: x ![]() R and x
R and x ![]() 6}
6}
Solution 3

Since, x ![]() {whole numbers}
{whole numbers}
![]() Solution set = {0, 1, 2, 3, 4}
Solution set = {0, 1, 2, 3, 4}
Solution 4
7x + 3![]() 3x - 5
3x - 5
4x ![]() -8
-8
x ![]() -2
-2
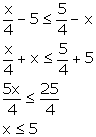
Since, x ![]() N
N
![]() Solution set = {1, 2, 3, 4, 5}
Solution set = {1, 2, 3, 4, 5}
Solution 5
(i) ![]()
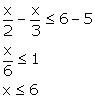
Since, x is a positive odd integer
![]() Solution set = {1, 3, 5}
Solution set = {1, 3, 5}
(ii) ![]()
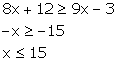
Since, x is a positive even integer
![]() Solution set = {2, 4, 6, 8, 10, 12, 14}
Solution set = {2, 4, 6, 8, 10, 12, 14}
Solution 6
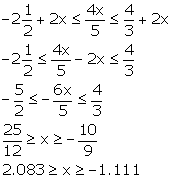
Since, x ![]() W
W
![]() Solution set = {0, 1, 2}
Solution set = {0, 1, 2}
The solution set can be represented on number line as:
![]()
Solution 7
Let the required integers be x, x + 1 and x + 2.
According to the given statement,
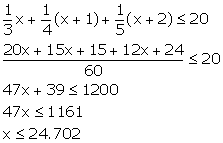
Thus, the largest value of the positive integer x is 24.
Hence, the required integers are 24, 25 and 26.
Solution 8
Consider the given inequation:

⇒ -4 ≤ x < 5; where x ∊ R
The solution set can be represented on a number line as follows:

Solution 9

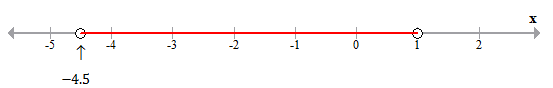
Solution 10
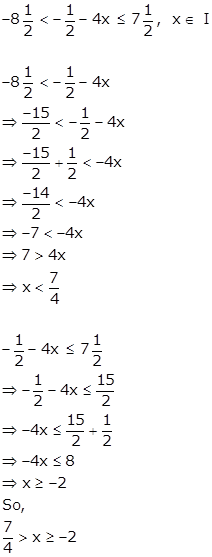
As, ![]()
![]()