Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 6 - Introduction to Euclid's Geometry
Introduction to Euclid's Geometry Exercise MCQ
Solution 1
Correct option: (b)
Squares and circular altars were used for household rituals.
Whereas altars having shapes as combinations of rectangles, triangles and trapeziums were used for public worship.
Solution 2
Correct option: (b)
In ancient India, altars with combination of shapes like rectangles, triangles and trapeziums were used for public rituals.
Solution 3
Correct option: (c)
The Sriyantra consists of nine interwoven isosceles triangles.
Solution 4
Correct option: (b)
In Indus Valley Civilization (about 300 BC) the bricks used for construction work were having dimensions in the ratio is 4:2:1.
Solution 5
Correct option: (a)
The famous treatise 'The Elements' was divided into 13 chapters by Euclid.
Solution 6
Correct option: (b)
Euclid belongs to the country, Greece.
Solution 7
Correct option: (c)
Thales belongs to the country, Greece.
Solution 8
Correct option: (b)
Pythagoras was a student of Thales.
Solution 9
Correct option: (d)
A statement that requires a proof is called a theorem.
Solution 10
Correct option: (a)
'Lines are parallel if they do not intersect' is started in the form of a definition.
Solution 11
Correct option: (c)
Euclid stated that 'All right angles are equal to each other' in the form of a postulate.
This is Euclid's Postulate 4.
Note: The answer in the book is option (a). But if you have a look at the Euclid's postulate, the answer is a postulate.
Solution 12
Correct option: (d)
A pyramid is a solid figure, whose base is any polygon.
Solution 13
Correct option: (a)
The side faces of a pyramid are triangles.
Solution 14
Correct option: (c)
A solid has 3 dimensions.
Solution 15
Correct option: (b)
A surface has 2 dimensions.
Solution 16
Correct option: (a)
A point is an exact location. A fine dot represents a point. So, a point has 0 dimensions.
Solution 17
Correct option: (c)
Boundaries of solids are surfaces.
Solution 18
Correct option: (b)
Boundaries of surfaces are curves.
Solution 19
Correct option: (d)
The number of planes passing through three non-collinear points is 1.
Solution 20
Correct option: (d)
Axioms are assumed as universal truths in all branches of mathematics because they are taken for granted, without proof.
Solution 21
Correct option: (c)
Two lines are said to be parallel, if they have no point in common.
Options (a), (b) and (d) have a common point, hence they are not parallel.
In option (c), the floor and the ceiling of a room are parallel to each other is a true statement.
Solution 22
Correct option: (c)
In option (a), infinite number of line can be drawn to pass through a given point. So, it is not a true statement.
In option (b), only one line can be drawn to pass through two given points. So, it is not a true statement.
In option (c),
'If two circles are equal, then their radii are equal' is the true statement.
In option (d), A line has no end points. A line has an indefinite length. So, it is not a true statement.
Solution 23
Correct option: (c)
Option (a) is true, since we can pass an infinite number of lines through a given point.
Option (b) is true, since a unique line can be drawn to pass through two given points.
Consider option (c).


As shown in the above diagram, a ray has only one end-point. So, option (d) is true.
Hence, the only false statement is option (c).
Solution 24
Correct option: (c)
A point C is called the midpoint of a line segment ![]() , if C is an interior point of AB such that
, if C is an interior point of AB such that ![]() =
=![]() .
.

Solution 25
Correct option: (d)

Observe the above figure. Clearly, C lies between A and B if AC + CB = AB.
That means, points A, B, C are collinear.
Solution 26
Correct option: (b)
Euclid's second axiom states that 'If equals are added to equals, the wholes are equal'.
Hence, when x + y = 15, then x + y + z = 15 + z.
Solution 27
Correct option: (a)
Euclid's first axiom states that 'Things which are equal to the same thing are equal to one another'.
That is,
A's age = B's age and C's age = B' age
⇒ A's age = C's age
Introduction to Euclid's Geometry Exercise Ex. 6
Solution 1
A theorem is a statement that requires a proof. Whereas, a basic fact which is taken for granted, without proof, is called an axiom.
Example of Theorem: Pythagoras Theorem
Example of axiom: A unique line can be drawn through any two points.
Solution 2
(i) Line segment: The straight path between two points is called a line segment.
(ii) Ray: A line segment when extended indefinitely in one direction is called a ray.
(iii) Intersecting Lines: Two lines meeting at a common point are called intersecting lines, i.e., they have a common point.
(iv) Parallel Lines: Two lines in a plane are said to be parallel, if they have no common point, i.e., they do not meet at all.
(v) Half-line: A ray without its initial point is called a half-line.
(vi) Concurrent lines: Three or more lines are said to be concurrent, if they intersect at the same point.
(vii) Collinear points: Three or more than three points are said to be collinear, if they lie on the same line.
(viii) Plane: A plane is a surface such that every point of the line joining any two points on it, lies on it.
Solution 3
(i) Six points: A,B,C,D,E,F
(ii)
Five line segments: ![]()
(iii)
Four rays: ![]()
(iv)
Four lines: ![]()
(vi) Four collinear points: M,E,G,B
Solution 4
(i) ![]() and their corresponding point of intersection is R.
and their corresponding point of intersection is R.
![]() and their corresponding point of intersection is P.
and their corresponding point of intersection is P.
(ii)
![]() and their point of intersection is R.
and their point of intersection is R.
(iii) Three rays are:
![]() .
.
(iv) Two line segments are:
![]() .
.
Solution 5
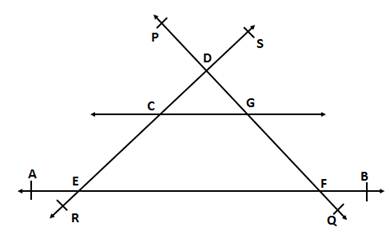
(i) Three lines: Line AB, Line PQ and Line RS
(ii) One rectilinear figure: EFGC
(iii) Four concurrent points: Points A, E, F and B
Solution 6
(i) An infinite number of lines can be drawn to pass through a given point.
(ii) One and only one line can pass through two given points.
(iii) Two given lines can at the most intersect at one and only one point.
(iv)
![]()
Solution 7
(i) False
(ii) False
(iii) False
(iv) True
(v) False
(vi) True
(vii) True
(viii) True
(ix) True
(x) True
(xi) False
(xii) True
Solution 8

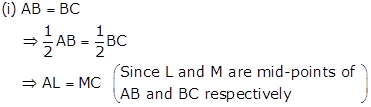
(ii) BL = BM
⇒ 2BL = 2BM
⇒ AB = BC

