Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 9 - Congruence of Triangles and Inequalities in a Triangle
Congruence of Triangles and Inequalities in a Triangle Exercise MCQ
Solution 1
Correct option: (a)
SSA is not a criterion for congruence of triangles.
Solution 2
Correct option: (c)
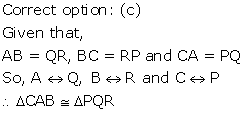
Solution 3
![]()
Solution 4
Correct option: (c)
In ΔABC,
AB = AC
⇒ ∠C = ∠B (angles opposite to equal sides are equal)
⇒ ∠C = 50°
Now, ∠A + ∠B + ∠C = 180°
⇒ ∠A + 50° + 50° = 180°
⇒ ∠A = 80°
Solution 5
Correct option: (a)
In ΔABC,
BC = AB
⇒ ∠A = ∠C (angles opposite to equal sides are equal)
Now, ∠A + ∠B + ∠C = 180°
⇒ ∠A + 80° + ∠A = 180°
⇒ 2∠A = 100°
⇒ ∠A = 50°
Solution 6
Correct option: (a)
In ΔABC,
∠C = ∠A
⇒ AB = BC (sides opposite to equal angles are equal)
⇒ AB = 4 cm
Solution 7
Correct option: (b)
The sum of any two sides of a triangle is greater than the third side.
Since, 4 cm + 2.5 cm = 6.5 cm
The length of third side of a triangle cannot be 6.5 cm.
Solution 8
Correct option: (b)
We know that in a triangle, the greater angle has the longer side opposite to it.
In ΔABC,
∠C > ∠B
⇒ AB >AC
Solution 9

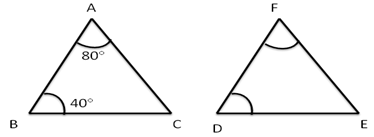
Solution 10

Solution 11
Correct option: (c)

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Congruence of Triangles and Inequalities in a Triangle Exercise Ex. 9B
Solution 1(i)
No, it is not possible to construct a triangle with lengths of its sides given because the sum of two sides, 5 cm and 4 cm, is not greater than the third side, 9 cm.
Solution 1(ii)
Yes, it is not possible to construct a triangle with lengths of its sides given because the sum of any two sides is greater than the third side.
Solution 1(iii)
Yes, it is not possible to construct a triangle with lengths of its sides given because the sum of any two sides is greater than the third side.
Solution 1(iv)
Yes, it is not possible to construct a triangle with lengths of its sides given because the sum of any two sides is greater than the third side.
Solution 1(v)
No, it is not possible to construct a triangle with lengths of its sides given because the sum of two sides, 3 cm and 4 cm, is not greater than the third side, 8 cm.
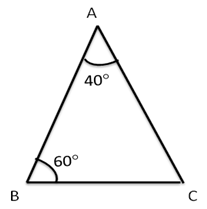
Solution 2
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ 50° + 60° + ∠C = 180°
⇒ ∠C = 70°
Thus, we have
∠A < ∠B < ∠C
⇒ BC < AC < AB
Hence, the longest side is AB and the shortest side is BC.
Solution 3(iii)
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ 100° + ∠B + 50° = 180°
⇒ ∠B = 30°
Thus, we have
∠B < ∠C < ∠A
⇒ AC < AB < BC
Hence, the shortest side is AC.
Solution 3(i)

Solution 3(ii)

Solution 4
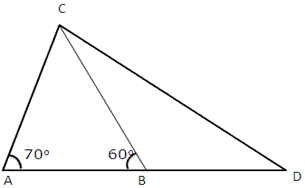

Solution 5
In ΔAOB,
∠B < ∠A
⇒ AO < BO ….(i)
In ΔCOD,
∠C < ∠D
⇒ DO < CO ….(ii)
Adding (i) and (ii),
AO + DO < BO + CO
⇒ AD < BC
Solution 6
Construction: Join AC and BD.
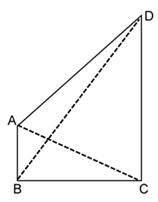
In ΔABC,
BC > AB
⇒ ∠BAC > ∠ACB ….(i)
In ΔACD,
CD > AD
⇒ ∠CAD > ∠ACD ….(ii)
Adding (i) and (ii), we get
∠BAC + ∠CAD > ∠ACB + ∠ACD
⇒ ∠A > ∠C
In ΔADB,
AD > AB
⇒ ∠ABD > ∠ADB ….(iii)
In ΔBDC,
CD > BC
⇒ ∠CBD > ∠BDC ….(iv)
Adding (iii) and (iv), we get
∠ABD + ∠CBD > ∠ADB + ∠BDC
⇒ ∠B > ∠D
Solution 7
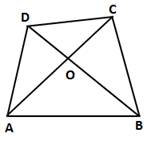
In ΔABC,
AB + BC > AC ….(i)
In ΔACD,
DA + CD > AC ….(ii)
In ΔADB,
DA + AB > BD ….(iii)
In ΔBDC,
BC + CD > BD ….(iv)
Adding (i), (ii), (iii) and (iv), we get
AB + BC + DA + CD + DA + AB + BC + CD > AC + AC + BD + BD
⇒ 2(AB + BC + CD + DA) > 2(AC + BD)
⇒ AB + BC + CD + DA > AC + BD
Solution 8

In ΔAOB,
AO + BO > AB ….(i)
In ΔBOC,
BO + CO > BC ….(ii)
In ΔCOD,
CO + DO > CD ….(iii)
In ΔAOD,
DO + AO > DA ….(iv)
Adding (i), (ii), (iii) and (iv), we get
AO + BO + BO + CO + CO + DO + DO + AO > AB + BC + CD + DA
⇒ 2(AO + CO) + 2(BO + DO) > AB + BC + CD + DA
⇒ 2AC + 2BD > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA
⇒ AB + BC + CD + DA < 2(AC + BD)
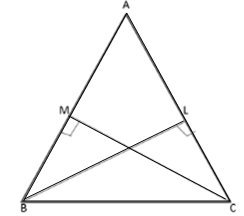
Solution 9
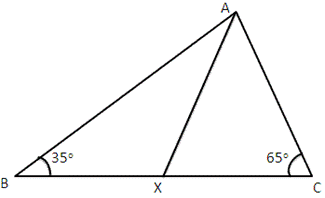
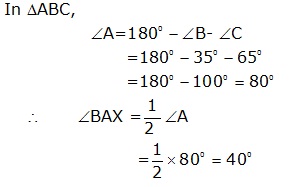
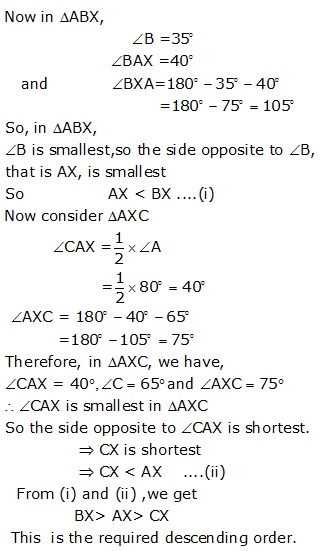
Solution 10
In ΔPQR,
PQ > PR
⇒ ∠PRQ > ∠PQR
![]()
⇒ ∠SRQ > ∠SQR
⇒ SQ > SR
Solution 11

In ΔABC,
AB = AC
⇒ ∠ABC = ∠ACB ….(i)
Now, ∠ABC = ∠ABD + ∠DBC
⇒ ∠ABC > ∠DBC
⇒ ∠ACB > ∠DBC [From (i)]
⇒ ∠DCB > ∠DBC
⇒ BD > CD
i.e. CD < BD
Solution 12
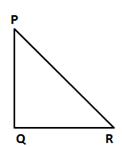
Let PQR be the required triangle.
Let PR be the longest side.
Then, PR > PQ
⇒ ∠Q > ∠R ….(i)
Also, PR > QR
⇒ ∠Q > ∠P ….(ii)
Adding (i) and (ii), we get
2∠Q > ∠R + ∠P
⇒ 2∠Q + ∠Q > ∠P + ∠Q + ∠R (adding ∠Q to both sides)
⇒ 3∠Q > 180°
⇒ ∠Q > 60°
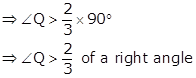
Solution 13(i)
In ΔCDA,
CD + DA > AC ….(i)
In ΔABC,
AC + AB > BC ….(ii)
Adding (i) and (ii), we get
CD + DA + AC + AB > AC + BC
Subtracting AC from both sides, we get
CD + DA + AB > BC
Solution 13(ii)
In ΔCDA,
CD + DA > AC ….(i)
In ΔABC,
AB + BC > AC ….(ii)
Adding (i) and (ii), we get
CD + DA + AB + BC > AC + AC
⇒ CD + DA + AB + BC > 2AC
Solution 14(i)
Given : ABC is a triangle and O is appoint insideit.
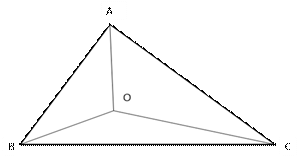
To Prove : (i) AB+AC > OB +OC
Solution 14(ii)
AB+BC+CA > OA+OB+OC
Solution 14(iii)
OA+OB+OC> ![]() (AB+BC+CA)
(AB+BC+CA)
Proof:
(i)In![]() ABC,
ABC,
AB+AC>BC.(i)
And in , ![]() OBC,
OBC,
OB+OC>BC.(ii)
Subtracting (i) from (i) we get
(AB+AC)-(OB+OC)> (BC-BC)
i.e.AB+AC>OB+OC
(ii)AB+AC> OB+OC[proved in (i)]
Similarly,AB+BC > OA+OC
AndAC+BC> OA +OB
Addingboth sides of these three inequalities, we get
(AB+AC) +(AC+BC) +(AB+BC)>OB+OC+OA+OB+OA+OC
i.e.2(AB+BC+AC)> 2(OA+OB+OC)
Therefore, we have
AB+BC+AC > OA+OB+OC
(iii)In![]() OAB
OAB
OA+OB > AB(i)
In![]() OBC,
OBC,
OB+OC > BC(ii)
And, in ![]() OCA,
OCA,
OC+OA>CA
Adding (i), (ii) and (iii)we get
(OA+OB) + (OB+OC)+(OC+OA)> AB+BC+CA
i.e2(OA+OB+OC) > AB+BC+CA
![]() OA+OB+OC>
OA+OB+OC> ![]() (AB+BC+CA)
(AB+BC+CA)
Solution 15
Construction: Mark a point S on BC such that BD = SD. Join AS.
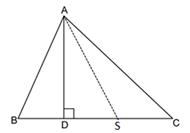
In ΔADB and ΔADS,
BD = SD (by construction)
∠ADB = ∠ADS (Each equal to 90°)
AD = AD (common)
∴ ΔADB ≅ ΔADS (by SAS congruence criterion)
⇒ AB = AS (c.p.c.t.)
Now, in ΔABS,
AB = AS
⇒ ∠ASB = ∠ABS ….(i)(angles opposite to equal sides are equal)
In ΔACS,
∠ASB > ∠ACS ….(ii)
From (i) and (ii), we have
∠ABS > ∠ACS
⇒ ∠ABC > ∠ACB
⇒ AC > AB
Solution 16
In ΔABC,
AB + AC > BC
⇒ AB + AC >BD + DC
⇒ AB + AC >BD + DE ….(i) [since CD = DE]
In ΔBED,
BD + DE > BE ….(ii)
From (i) and (ii), we have
AB + AC > BE
Congruence of Triangles and Inequalities in a Triangle Exercise Ex. 9A
Solution 1
(i) In ΔAOB and ΔDOC,
∠BAO = ∠CDO (AB ∥ CD, alternate angles)
AO = DO (O is the mid-point of AD)
∠AOB = ∠DOC (vertically opposite angles)
∴ ΔAOB ≅ ΔDOC (by ASA congruence criterion)
(ii) Since ΔAOB ≅ ΔDOC,
BO = CO (c.p.c.t.)
⇒ O is the mid-point of BC.
Solution 2
In ΔAOD and ΔBOC,
∠AOD = ∠BOC (vertically opposite angles)
∠DAO = ∠CBO (Each 90°)
AD = BC (given)
∴ ΔAOD ≅ BOC (by AAS congruence criterion)
⇒ AO = BO (c.p.c.t.)
⇒ CD bisects AB.
Solution 3
In ΔABC and ΔCDA
∠BAC = ∠DCA (alternate interior angles for p ∥ q)
AC = CA (common)
∠BCA = ∠DAC (alternate interior angles for l ∥ m)
∴ ΔABC ≅ ΔCDA (by ASA congruence rule)
Solution 4
(i) In ΔBAD and ΔCAD
∠ADB = ∠ADC (Each 90° as AD is an altitude)
AB = AC (given)
AD = AD (common)
∴ ΔBAD ≅ ΔCAD (by RHS Congruence criterion)
⇒ BD = CD (c.p.c.t.)
Hence AD bisects BC.
(ii) Also, ∠BAD = ∠CAD (c.p.c.t.)
Hence, AD bisects ∠A.
Solution 5
(i) In ΔABE and ΔACF,
∠AEB = ∠AFC (Each 90°)
BE = CF (given)
∠BAE = ∠CAF (common ∠A)
∴ ΔABE ≅ ACF (by ASA congruence criterion)
(ii) Since ΔABE ≅ ΔACF,
AB = AC (c.p.c.t.)
Solution 6
(i) In ΔABD and ΔACD,
AB = AC (equal sides of isosceles ΔABC)
DB = DC (equal sides of isosceles ΔDBC)
AD = AD (common)
∴ ΔABD ≅ ACD (by SSS congruence criterion)
(ii) Since ΔABD ≅ ΔACD,
∠BAD = ∠CAD (c.p.c.t.)
⇒ ∠BAE = ∠CAE ….(1)
Now, in ΔABE and ΔACE
AB = AC (equal sides of isosceles ΔABC)
∠BAE = ∠CAE [From (1)]
AE = AE (common)
∴ ΔABE ≅ ACE (by SAS congruence criterion)
(iii) Since ΔABD ≅ ΔACD,
∠BAD = ∠CAD (c.p.c.t.)
⇒ ∠BAE = ∠CAE
Thus, AE bisects ∠A.
In ΔBDE and ΔCDE,
BD = CD (equal sides of isosceles ΔABC)
BE = CE (c.p.c.t. since ΔABE ≅ ACE)
DE = DE (common)
∴ ΔBDE ≅ CDE (by SSS congruence criterion)
⇒ ∠BDE = ∠CDE (c.p.c.t.)
Thus, DE bisects ∠D, i.e., AE bisects ∠D.
Hence, AE bisects ∠A as well as ∠D.
(iv) Since ΔBDE ≅ ΔCDE,
BE = CE and ∠BED = ∠CED (c.p.c.t.)
⇒ BE = CE and ∠BED = ∠CED = 90° (since ∠BED and ∠CED form a linear pair)
⇒ DE is the perpendicular bisector of BC.
⇒ AE is the perpendicular bisector of BC.
Solution 7
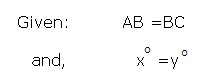

Solution 8
(i) In ΔAPB and ΔAQB,
∠APB = ∠AQC (Each 90°)
∠BAP = ∠BAQ (line l is the bisector of ∠A)
AB = AB (common)
∴ ΔAPB ≅ AQB (by AAS congruence criterion)
(ii) Since ΔAPB ≅ ΔAQB,
BP = BQ (c.p.c.t.)
Solution 9

In ΔABC and ΔADC,
∠BAC = ∠DAC (AC bisects ∠A)
AC = AC (common)
∠BCA = ∠DCA (AC bisects ∠C)
∴ ΔABC ≅ ADC (by ASA congruence criterion)
⇒ AB = AD and CB = CD (c.p.c.t.)
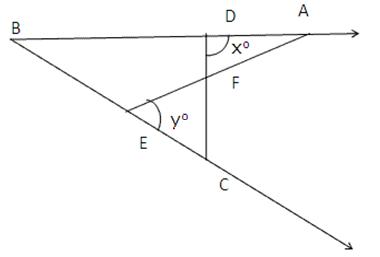
Solution 10
Construction: Draw DE ⊥ BC.
In ΔDAC and ΔDEC,
∠DAC = ∠DEC (Each 90°)
∠DCA = ∠DCE (CD bisects ∠C)
CD = CD (common)
∴ ΔDAC ≅ ΔDEC (by AAS congruence criterion)
⇒ DA = DE (c.p.c.t.) ….(i)
and AC = EC (c.p.c.t.) ….(ii)
Given, AB = AC
⇒ ∠B = ∠C (angles opposite to equal sides are equal)
In ΔABC, by angle sum property,
∠A + ∠B + ∠C = 180°
⇒ 90° + ∠B + ∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
In ΔBED,
∠BDE + ∠B = 90° (since ∠BED = 90°)
⇒ ∠BDE + 45° = 90°
⇒ ∠BDE = 45°
⇒ ∠BDE = ∠DBE = 45°
⇒ DE = BE ….(iii)
From (i) and (iii),
DA = DE = BE ….(iv)
Now, BC = BE + EC
⇒ BC = DA + AC [From (ii) and (iv)
⇒ AC + AD = BC
Solution 11
![]()

Solution 12
![]()
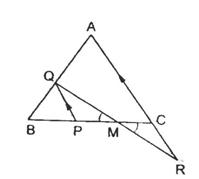

Solution 13
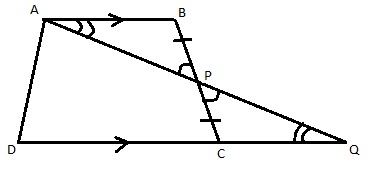

Solution 14
![]()
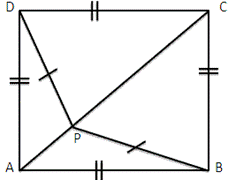

Solution 15
ΔOAB is an equilateral triangle.
⇒ ∠OAB = ∠OBA = AOB = 60°
ABCD is a square.
⇒ ∠A = ∠B = ∠C = ∠D = 90°
Now, ∠A = ∠DAO + ∠OAB
⇒ 90° = ∠DAO + 60°
⇒ ∠DAO = 90° - 60° = 30°
Similarly, ∠CBO = 30°
In ΔOAD and ΔOBC,
AD = BC (sides of a square ABCD)
∠DAO = ∠CBO = 30°
OA = OB (sides of an equilateral ΔOAB)
∴ ΔOAD ≅ ΔOBC (by SAS congruence criterion)
⇒ OD = OC (c.p.c.t.)
Hence, ΔOCD is an isosceles triangle.
Solution 16
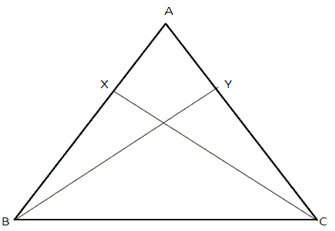

Solution 17
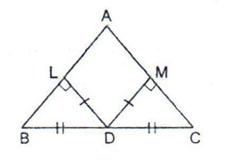


Solution 18
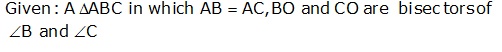

Solution 19
Construction: Join AN and BN.

In ΔANM and ΔBNM
AM = BM (M is the mid-point of AB)
∠AMN = ∠BMN (Each 90°)
MN = MN (common)
∴ ΔANM ≅ ΔBNM (by SAS congruence criterion)
⇒ AN = BN (c.p.c.t.) ….(i)
And, ∠ANM = ∠BNM (c.p.c.t.)
⇒ 90° - ∠ANM = 90° - ∠BNM
⇒ ∠AND = ∠BNC ….(ii)
In ΔAND and DBNC,
AN = BN [From (i)]
∠AND = ∠BNC [From (ii)]
DN = CN (N is the mid-point of DC)
∴ ΔAND ≅ ΔBNC (by SAS congruence criterion)
⇒ AD = BC (c.p.c.t.)
Solution 20
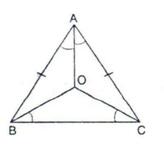
In ΔABC, AB = AC
⇒ ∠ABC = ∠ACB
![]()
⇒ ∠OBC = ∠OCB ….(i)
Now, by exterior angle property,
∠MOC = ∠OBC + ∠OCB
⇒ ∠MOC = 2∠OBC [From (i)]
⇒ ∠MOC = ∠ABC (OB is the bisector of ∠ABC)
Solution 21
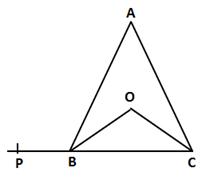
In ΔABC, AB = AC
⇒ ∠ABC = ∠ACB
![]()
⇒ ∠OBC = ∠OCB ….(i)
In ΔBOC, by angle sum property,
∠BOC + ∠OBC + ∠OCB = 180°
⇒ ∠BOC + 2∠OBC = 180° [From (i)]
⇒ ∠BOC + ∠ABC = 180°
⇒ ∠BOC + (180° - ∠ABP) = 180° (∠ABC and ∠ABP form a linear pair)
⇒ ∠BOC + 180° - ∠ABP = 180°
⇒ ∠BOC - ∠ABP = 0
⇒ ∠BOC = ∠ABP
Solution 22

AB ∥ PQ and BP is a transversal.
⇒ ∠ABP = ∠BPQ (alternate angles) ….(i)
BP is the bisector of ∠ABC.
⇒ ∠ABP = ∠PBC
⇒ ∠ABP = ∠PBQ ….(ii)
From (i) and (ii), we have
∠BPQ = ∠PBQ
⇒ PQ = BQ (sides opposite to equal angles are equal)
⇒ ΔBPQ is an isosceles triangle.
Solution 23
To prove that the image is as far behind the mirror as the object is in front of the mirror, we need to prove that AT = BT.
We know that angle of incidence = angle of reflection.
⇒ ∠ACN = ∠DCN ….(i)
AB ∥ CN and AC is the transversal.
⇒ ∠TAC = ∠ACN (alternate angles) ….(ii)
Also, AB ∥ CN and BD is the transversal.
⇒ ∠TBC = ∠DCN (corresponding angles) ….(iii)
From (i), (ii) and (iii),
∠TAC = ∠TBC ….(iv)
In ΔACT and ΔBCT,
∠TAC = ∠TBC [From (iv)]
∠ATC = ∠BTC (Each 90°)
CT = CT (common)
∴ ΔACT ≅ ΔBCT (by AAS congruence criterion)
⇒ AT = BT (c.p.c.t.)
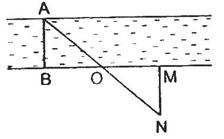
Solution 24
Let AB be the breadth of a river. Now take a point M on that bank of the river where point B is situated. Through M draw a perpendicular and take point N on it such that point, A, O and N lie on a straight line where point O is the mid point of BM.

Solution 25
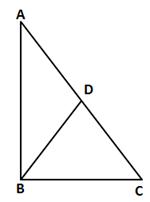
D is the mid-point of AC.
⇒ AD = CD = ![]()
Given,
BD = ![]()
⇒ AD = CD = BD
Consider AD = BD
⇒ ∠BAD = ∠ABD (i)(angles opposite to equal sides are equal)
Consider CD = BD
⇒ ∠BCD = ∠CBD (ii)(angles opposite to equal sides are equal)
In ΔABC, by angle sum property,
∠ABC + ∠BAC + ∠BCA = 180°
⇒ ∠ABC + ∠BAD + ∠BCD = 180°
⇒ ∠ABC + ∠ABD + ∠CBD = 180° [From (i) and (ii)]
⇒ ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
Hence, ∠ABC is a right angle.
Solution 26
The given statement is not true.
Two triangles are congruent if two sides and the included angle of one triangle are equal to corresponding two sides and the included angle of another triangle.
Solution 27
The given statement is not true.
Two triangles are congruent if two angles and the included side of one triangle are equal to corresponding two angles and the included angle of another triangle.

