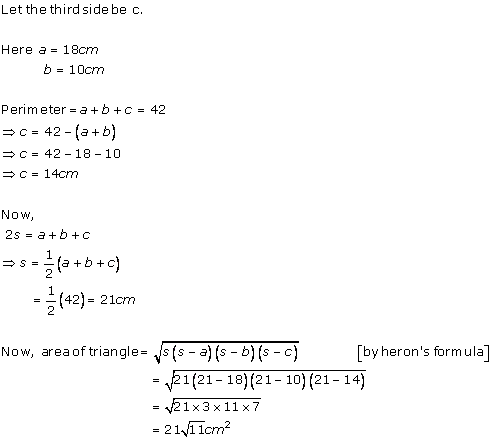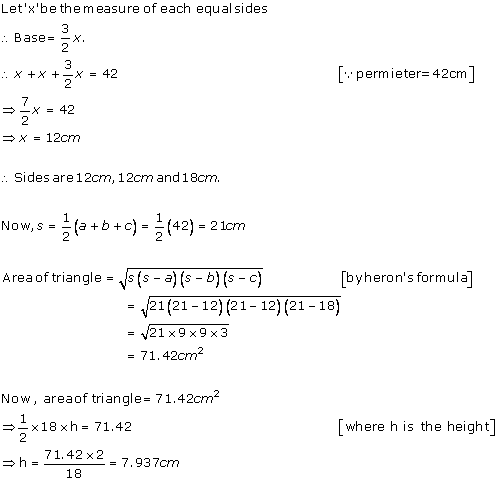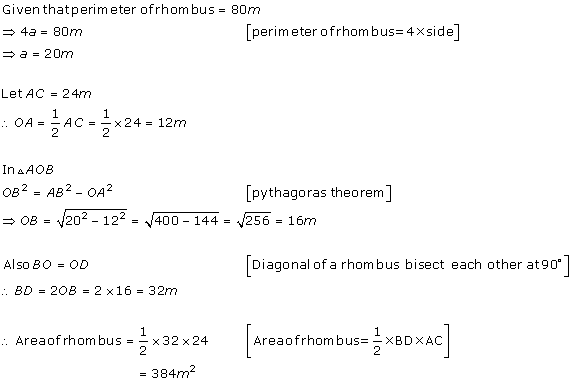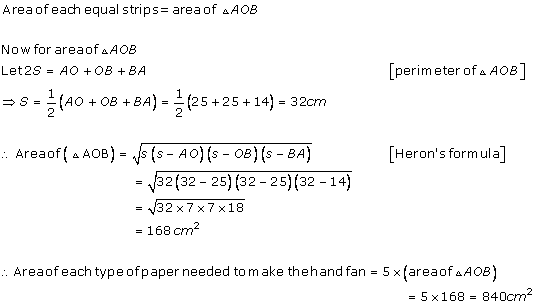Class 9 RD SHARMA Solutions Maths Chapter 17 - Heron's Formula
Ex. 17.1
Ex. 17.2
17.24
17.25
Heron's Formula Exercise Ex. 17.1
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
The sides of the triangular field are in the ratio 25:17:12.
Let the sides of triangle be 25x, 17x, and 12x.
Perimeter of this triangle = 540 m
25x + 17x + 12x = 540 m
54x = 540 m
x = 10 m
Sides of triangle will be 250 m, 170 m, and 120 m.
Let the sides of triangle be 25x, 17x, and 12x.
Perimeter of this triangle = 540 m
25x + 17x + 12x = 540 m
54x = 540 m
x = 10 m
Sides of triangle will be 250 m, 170 m, and 120 m.
Semi-perimeter (s) = 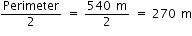
By Heron's formula:
So, area of the triangle is 9000 m2.
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Heron's Formula Exercise Ex. 17.2
Solution 1
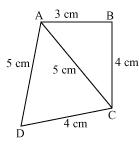
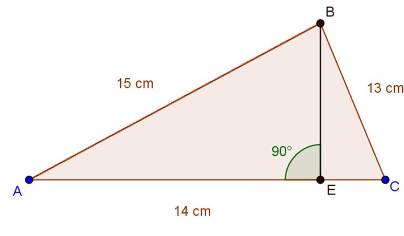
For  ABC
ABC
AC2 = AB2 + BC2
(5)2 = (3)2 + (4)2
So, ABC is a right angle triangle, right angled at point B.
ABC is a right angle triangle, right angled at point B.
Area of ABC
ABC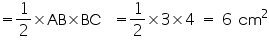
AC2 = AB2 + BC2
(5)2 = (3)2 + (4)2
So,
Area of
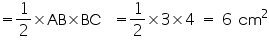
For  ADC
ADC
Perimeter = 2s = AC + CD + DA = (5 + 4 + 5) cm = 14 cm
s = 7 cm
By Heron's formula
Area of triangle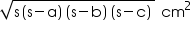
Perimeter = 2s = AC + CD + DA = (5 + 4 + 5) cm = 14 cm
s = 7 cm
By Heron's formula
Area of triangle

Area of ABCD = Area of  ABC + Area of
ABC + Area of  ACD
ACD
= (6 + 9.166) cm2 = 15.166 cm2 = 15.2 cm2 (approximately)
= (6 + 9.166) cm2 = 15.166 cm2 = 15.2 cm2 (approximately)
Solution 2

Solution 3
Solution 4
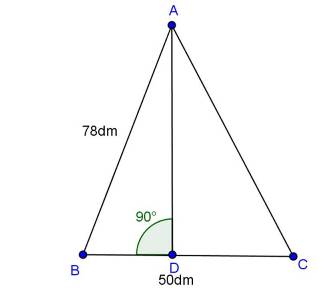
Let us join BD.
In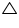 BCD applying Pythagoras theorem
BCD applying Pythagoras theorem
BD2 = BC2 + CD2
= (12)2 + (5)2
= 144 + 25
BD2 = 169
BD = 13 m
In
BD2 = BC2 + CD2
= (12)2 + (5)2
= 144 + 25
BD2 = 169
BD = 13 m
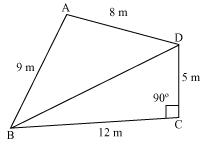
Area of 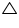 BCD
BCD
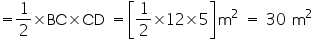
For 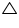 ABD
ABD
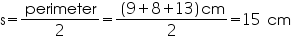
By Heron's formula 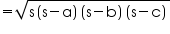
Area of triangle 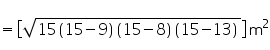
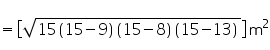
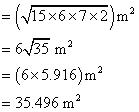
Area of park = Area of  ABD + Area of
ABD + Area of  BCD
BCD
= 35.496 + 30 m2
= 35.496 + 30 m2
= 65.496 m2
= 65. 5 m2 (approximately)
Solution 5
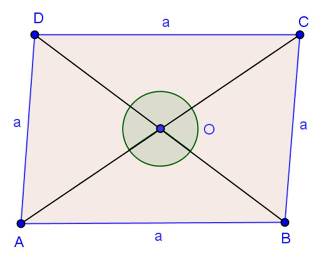
Solution 6

Solution 7

Solution 8
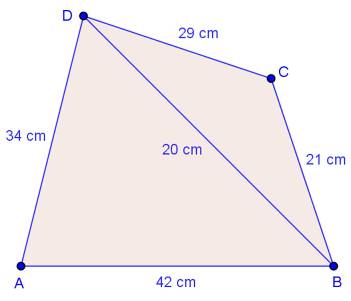
Solution 09
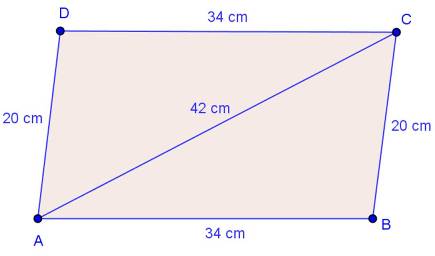
Solution 10
Solution 11

Solution 12
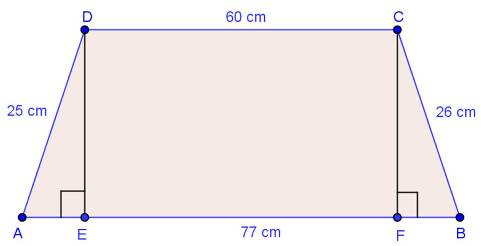
Solution 13
Solution 14
Heron's Formula Exercise 17.24
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5
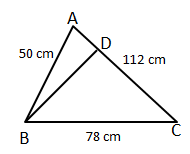

Heron's Formula Exercise 17.25
Solution 6

Solution 7

Solution 21
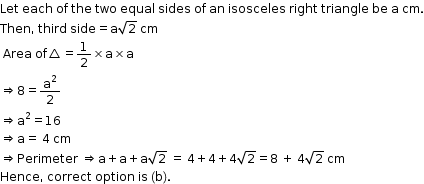
Solution 22

Solution 23
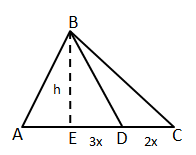

Solution 25

Solution 8
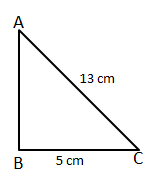
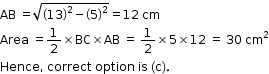
Solution 9

Solution 24

Solution 26