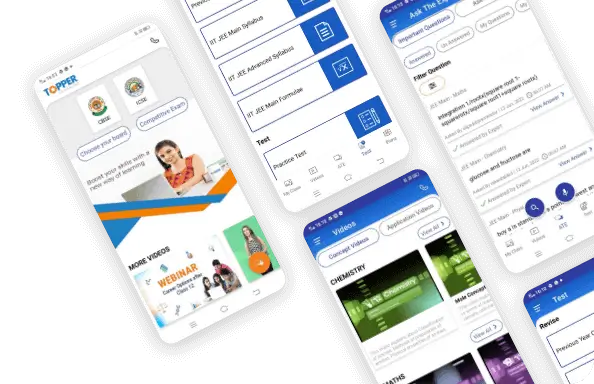
What are you preparing for?
Most Trending

9th Foundation
Build a solid conceptual foundation in Class 9 and 10 to ace the JEE and NEET exams.
Explore +
Class 8 CBSE
Discover many online study materials available, especially for Class 8 students.
Explore +
Class 10 ICSE
Explore the updated board exam study material from India's leading online learning platform.
Explore +
NEET
Boost confidence by practising numerous MCQs and subjective questions for the NEET exam.
Explore +TopperLearning: Leading Online Learning Platform for K12, CBSE, ICSE, JEE & NEET
Known as a pioneer for creating one of the most popular learning apps in the world, TopperLearning is India's most excellent education platform. An initiative of India's leading media conglomerate Network18. A conceptualised learning experience is offered by TopperLearning for 1st through 12th-grade students for CBSE and 6th through 10th-grade students for ICSE and State Boards. In addition to our updated content, we also provide extensive practice material to help aspirants prepare for competitive exams like NEET and JEE Main.
What are the benefits of studying with TopperLearning?
TopperLearning aims to make online education accessible and affordable. Students benefit from advanced and innovative learning resources.
- Accessible and Affordable Learning. Unique online studying experience with the best teachers.
- Creating a solid base for students aiming for competitive exams like JEE and NEET with Foundation courses for classes 9 and 10.
- Extensive study materials like Textbook solutions (FREE), Sample Papers, Important Questions, Revision Notes, Subjective Questions, Video Lessons, Mock Tests, and Multiple Choice Questions ensure regular practice for various subjects, including Maths, Social Studies, Physics, Chemistry, Biology, English, and Hindi.
- Study materials are prepared based on textbook solutions of NCERT, RD Sharma, RS Agarwal, HC Verma, and Selina Solutions, to name a few.
- With ASK a DOUBT app, students can search from over 3Lakh questions to find the answer to their question. Students can upload an image or type a question and get a step-wise detailed answer.
Importance of Online Learning
With a change in the students learning journey, they need to adapt. Online learning backs students with a better understanding of concepts than traditional learning methods. It makes students more confident and makes them understand challenging concepts more simply.
Why should Students enrol with Topperlearning?
Students must enrol with TopperLearning to gain confidence to score good marks in their examinations. Grasping concepts of Maths, innovation in doing science experiments, and learning about ancient history is not only made fun but also educational for students.
Our website and TopperLearning app allow them to download PDFs and study all the extensive subject material. Students can not only prepare for their CBSE & ICSE Board and school exams but also ace exams like JEE Main and NEET by taking Foundation courses in Classes 9 and 10 (Physics, Chemistry, Math, and Biology)
2 Million+
Toppers
6 Lakh+
Questions In Bank
13k+
Mapped Videos
98%
Elevated Scores

Test series with performance report

Video lessons by ivy league faculties

Unlimited practice

Simplified problem solving

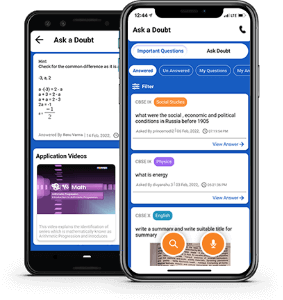
Ask a doubt
Ask a Doubt
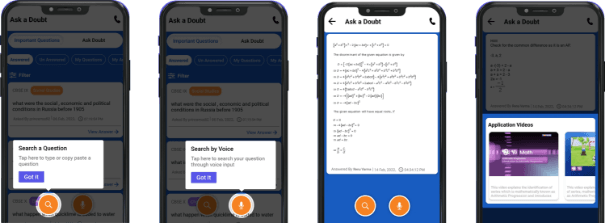
A one-stop solution for all your academic doubts, answered by experienced and qualified faculty members. The platform gives an ecosystem to search your answer by text or by a voice from the pool of already answered queries in a convenient way.

Our Partnership Programs
If you are a school, tuition centre, private tutor, innovative education entity or an investor who believes in providing quality education,
join us!

Ask A Doubt App
More than 3 lakh expert-verified answers are available here.
Frequently Asked Questions
Students can search for answers from 3L+ questions already answered by our experts by using the search feature on our website or downloading the Ask a Doubt app. They can also upload a question or image and ask a free question at Ask a Doubt. It is a free doubt-solving offering from TopperLearning, the leading online learning platform for students. Students can upload their queries about any subject or topic for comprehensive solutions, which our subject experts will address.
TopperLearning provides various subscriptions for online learning for students starting from just ₹999 annually. Students can check the latest offers and avail of subscription-based online learning.
TopperLearning is a constructive platform that provides numerous offerings. Textbook solutions, important questions, Revision notes, Sample papers, Previous year papers, Online test series, Ask a doubt, and more online study materials for K-12 classes of multiple boards, including CBSE, ICSE, and other State Boards. We also offer Foundation courses for NEET & JEE Main.
Yes, TopperLearning provides free access to demos for various online classes for students. Examining the free demo allows students to understand the study session. They can also register for free access to the best online study material.
Yes, the online study materials provided by TopperLearning are up to date. They are specially curated by subject experts and updated through multiple sources for different boards so that students can engage and learn efficiently.