Class 11-science RD SHARMA Solutions Maths Chapter 28 - Introduction to 3-D coordinate geometry
Introduction to 3-D coordinate geometry Exercise Ex. 28.1
Solution 1(i)
All are positive, so octant is XOYZ
Solution 1(ii)
X is negative and rest are positive, so octant is X'OYZ
Solution 1(iii)
Y is negative and rest are positive, so octant is XOY'Z
Solution 1(iv)
Z is negative and rest are positive, so octant is XOYZ'
Solution 1(v)
X and Y are negative and Z is positive, so octant is X'OY'Z
Solution 1(vi)
All are negative, so octant is X'OY'Z'
Solution 1(vii)
Y and Z are negative, so octant is XOY'Z'
Solution 1(viii)
X and Z are negative, so octant is X'OYZ'
Solution 2(i)
YZ plane is x-axis, so sign of x will be changed. So answer is (2, 3, 4)
Solution 2(ii)
XZ plane is y-axis, so sign of y will be changed. So answer is (-5, -4, -3)
Solution 2(iii)
XY-plane is z-axis, so sign of Z will change. So answer is (5, 2, 7)
Solution 2(iv)
XZ plane is y-axis, so sign of Y will change, So answer is (-5, 0, 3)
Solution 2(v)
XY plane is Z-axis, so sign of Z will change So answer is (-4, 0, 0)
Solution 3
Vertices of cube are
(1, 0, -1) (1, 0, 4) (1, -5, -1)
(1, -5, 4) (-4, 0, -1) (-4, -5, -4)
(-4, -5, -1) (4, 0, 4) (1, 0, 4)
Solution 4
3-(-2)=5, |0-5|=5, |-1-4|=5
5, 5, 5 are lengths of edges
Solution 5
5-3=2, 0-(-2)=2, 5-2=3
2, 2, 3 are lengths of edges
Solution 6
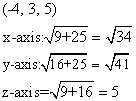
Solution 7
(-3, -2, -5) (-3, -2, 5) (3, -2, -5) (-3, 2, -5) (3, 2, 5)
(3, 2, -5) (-3, 2, 5)
Introduction to 3-D coordinate geometry Exercise Ex. 28.2
Solution 1

Solution 2

Solution 3(i)
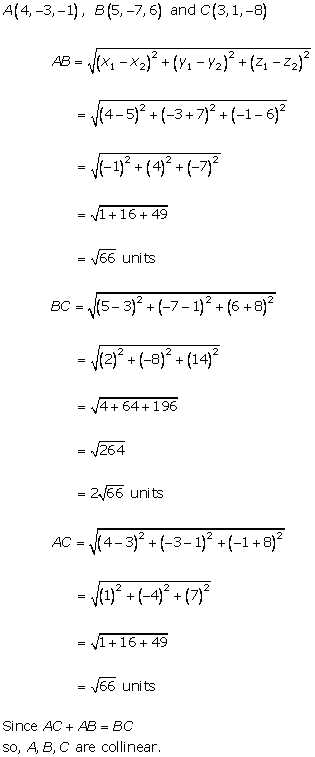
Solution 3(ii)

Solution 3(iii)

Solution 4(i)
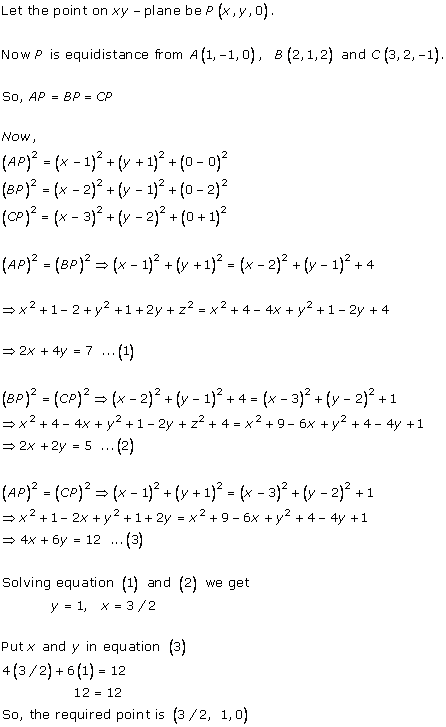
Solution 4(ii)
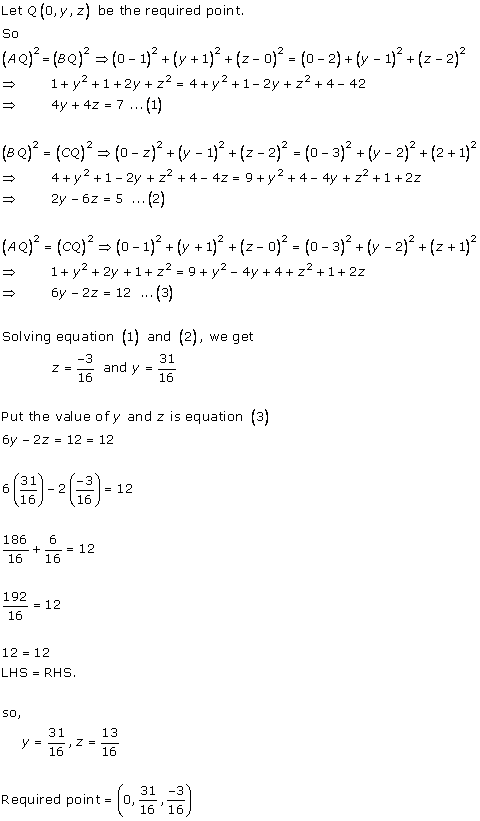
Solution 4(iii)

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
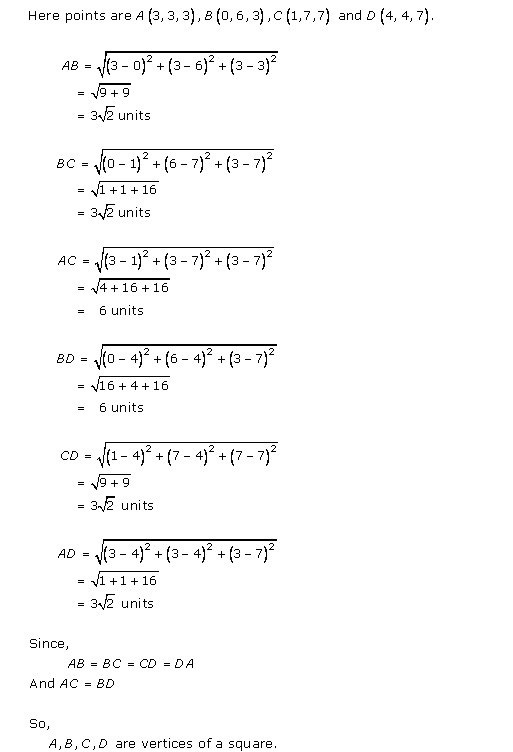
Solution 11

Solution 12

Solution 13

Solution 14
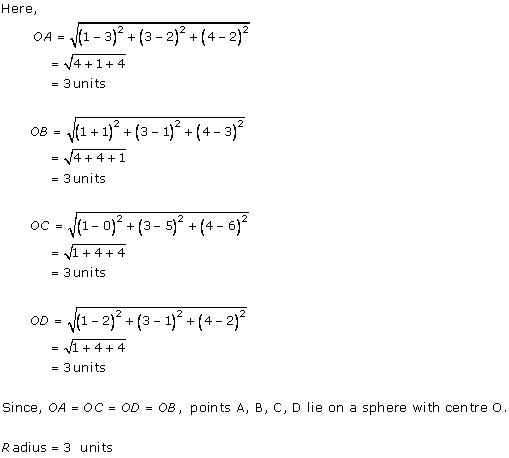
Solution 15
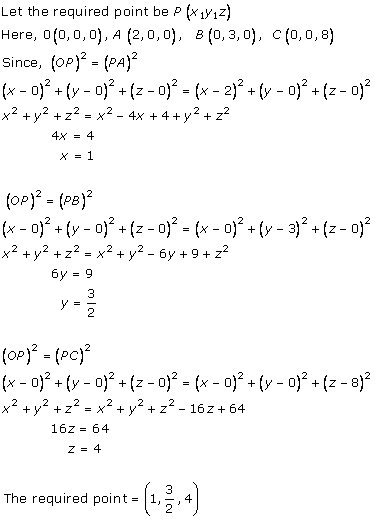
Solution 16

Solution 17

Solution 18

Solution 19

Solution 20(i)
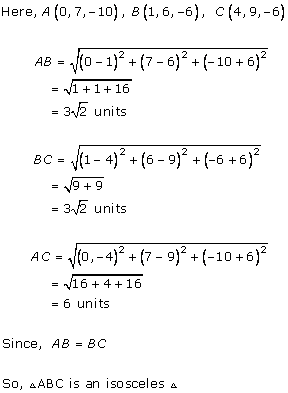
Solution 20(ii)

Solution 20(iii)

Solution 21

Solution 22
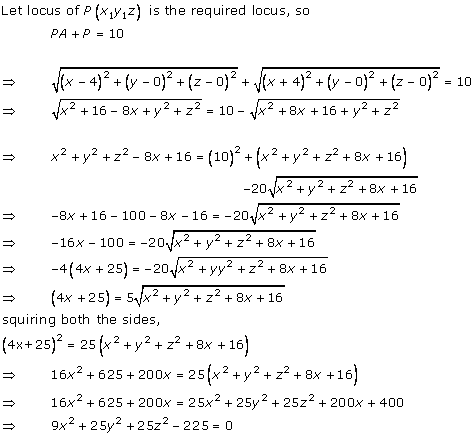
Solution 23
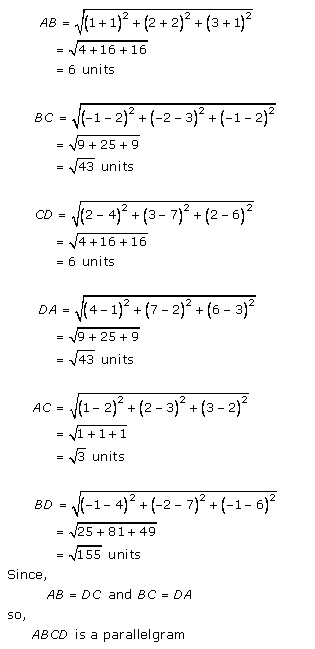
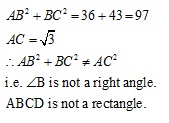
Solution 24
Solution 20(iv)
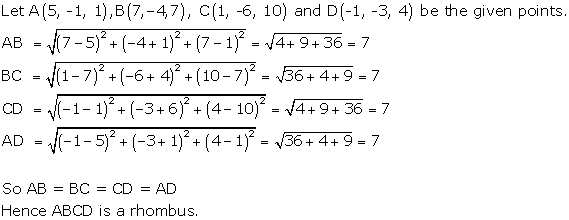
Introduction to 3-D coordinate geometry Exercise Ex. 28.3
Solution 1
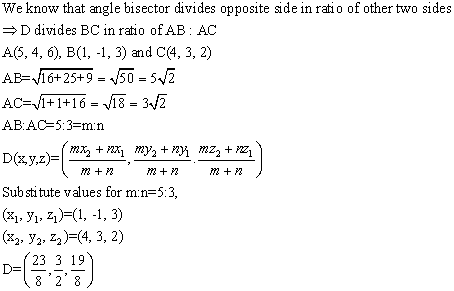
Solution 2

Solution 3

Solution 4
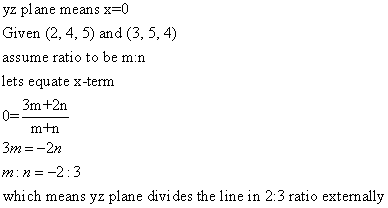
Solution 5

Solution 6
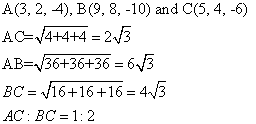
Solution 7

Solution 8
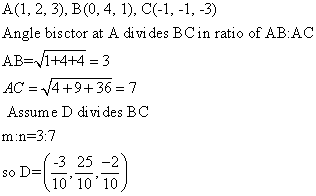
Solution 9

Solution 10

Solution 11

Solution 12
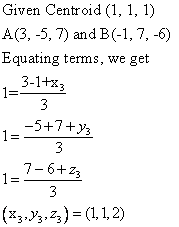
Solution 13

Solution 14

Solution 15

Solution 16



