Class 9 SELINA Solutions Maths Chapter 9 - Triangles [Congruency in Triangles]
Triangles [Congruency in Triangles] Exercise Ex. 9(A)
Solution 1(a)
Correct option: (i) AC = PR
ΔABC ≅ ΔPQR
Then, by c.p.c.t.
AB = PQ
BC = QR
AC = PR
Hence,
AC = PR.
Solution 1(b)
Correct option: (iii) angle BAC
In ΔABD and ΔACD
AB = AC … given
BD = CD … given
AD is common
∴ ΔABD ≅ ΔACD … (S.S.S.)
∴ ∠BAD = ∠CAD … (c.p.c.t.)
∴ AD bisects ∠BAC
Solution 1(c)
Correct option: (ii) CD = CB
In ΔADC and ΔABC
AD = AB … given
∠DAC = ∠BAC … given
AC is common
∴ ΔADC ≅ ΔABC … (S.S.S.)
∴ By c.p.c.t.
∠B = ∠D
∠ACD = ∠ACB
CD = CB
Solution 1(d)
Correct option: (iv) AM bisects ∠BAC
In ΔAMB and ΔAMC
AM is common
∠AMB = ∠AMC … each 90o
MB = MC … AM is the perpendicular bisector of BC
∴ ΔAMB ≅ ΔAMC … (S.A.S.)
∴ By c.p.c.t.
AB = AC
∠BAM = ∠CAM
∴ AM bisects ∠BAC
Solution 1(e)
Correct option: (iv) ΔABC @ ΔPQR
In ΔABM and ΔPQN
AB = PQ … given
AM = PN … given
BC = QR … given
∴ 2BM = 2QN … M and N are midpoints of BC and QR respectively
∴ .BM = QN
∴ ΔABM ≅ ΔPQN …(S.S.S.)
∴ ∠ABM = ∠PQN … (c.p.c.t.)
Now,
AB = PQ … given
BC = QR … given
∠ABC = ∠PQR
ΔABC ≅ ΔPQR … (S.A.S.)
Solution 2


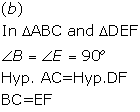






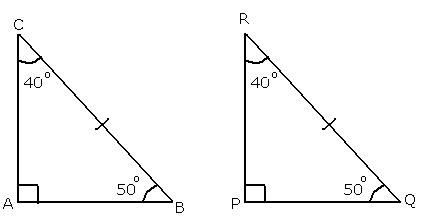

Solution 3

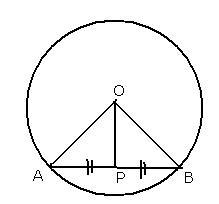

Solution 4



Solution 5
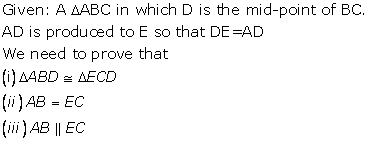


Solution 6
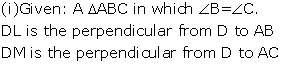


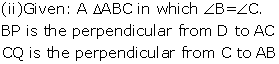
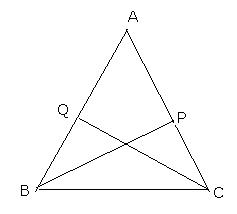

Solution 7

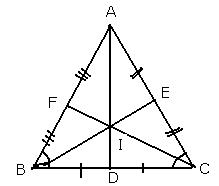


Solution 8
![]()


Solution 9
![]()
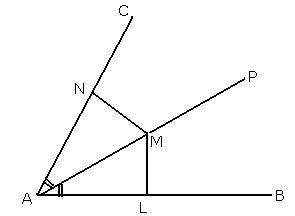

Solution 10
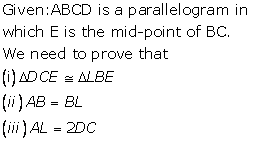
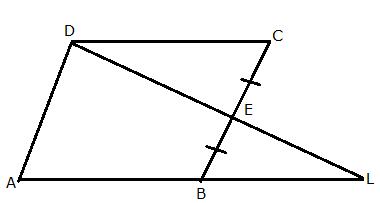


Triangles [Congruency in Triangles] Exercise Ex. 9(B)
Solution 1(a)
Correct option: (iii) AB and CD bisect each other
In, ΔACP and ΔBDP
AC = BD ... given
∠C = ∠D … each 90o
∠APC = ∠BPD … vertically opposite angles
ΔACP ≅ ΔBDP … (A.A.S.)
Then, by c.p.c.t.
CP = DP
AP = BP
Hence, AB and CD bisect each other
Solution 1(b)
Correct option: (ii) ΔABC ≅ ΔAED
In, ΔABC and ΔAED
∠BAD = ∠EAC ... given
∴ ∠BAD + ∠DAC = ∠EAC + ∠DAC
∴ ∠BAC = ∠EAD
BD = EC
∴ BD + DC = EC + DC
∴ BC = ED
∠B = ∠E … given
∴ ΔABC ≅ ΔAED … (A.A.S.)
Solution 1(c)
Correct option: (i) ΔABD ≅ ΔACD
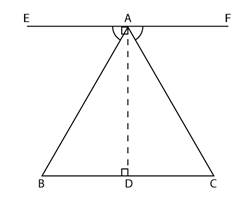
AD is ⊥ to both EF and BD.
Hence, EF || BD
Now, if AB is a transversal ∠EAB = ∠ABD…(alternate angles)
Similarly, if AC is a transversal
∠FAC = ∠ACD…(alternate angles)
Now,
∠EAB = ∠FAC … given
Hence,
∠ABD = ∠ACD… (1)
Now,
In, ΔABD and ΔACD
AD is common
∠ABD= ∠ACD … from (1)
∠ADB = ∠ADC … each 90o
ΔABD ≅ ΔACD … (A.A.S.)
Solution 1(d)
Correct option: (iii) BP = AR
Join PR
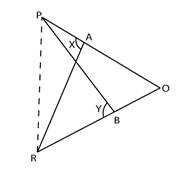
In ΔPOR
PO = RO
∠OPR = ∠ORP … angles opposite to equal sides in a triangle
In, ΔPAR and ΔRBP
∠x = ∠y … given
∠OPR = ∠ORP
PR is common
ΔPAR ≅ ΔRBP … (A.A.S.)
∴ BP = AR … (c.p.c.t.)
Solution 1(e)
Correct option: (i) AB and CD bisect each other
BC||DA
Now, if AB is a transversal ∠CBO = ∠DAO…(alternate angles)
Similarly, if CD is a transversal
∠BCO = ∠ADO…(alternate angles)
Also, BC = DA … given
Hence,
ΔCOB ≅ ΔDOA … (A.S.A.)
Then, by c.p.c.t.
CO = DO
BO = AO
Hence, AB and CD bisect each other
Solution 2



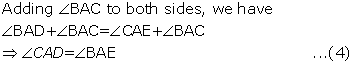


Solution 3









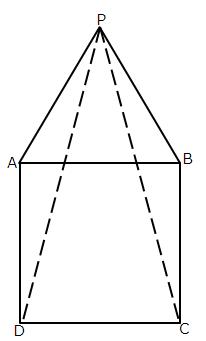







Solution 4
![]()
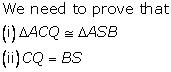
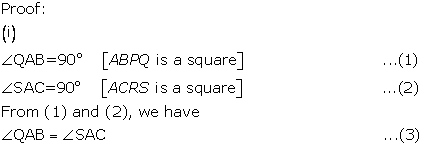
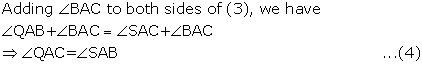

![]()
![]()
Solution 5

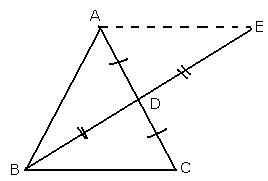
![]()

Solution 6
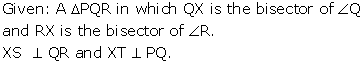

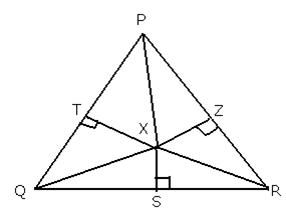



Solution 7
![]()
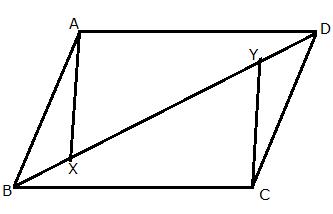


Solution 8

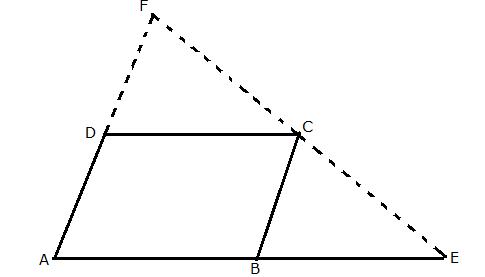

Solution 9

Solution 10


Solution 11


Solution 12
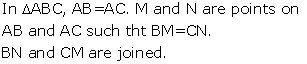
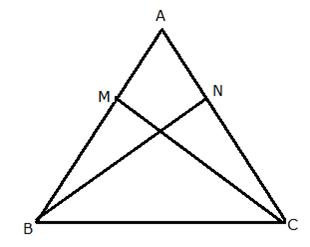
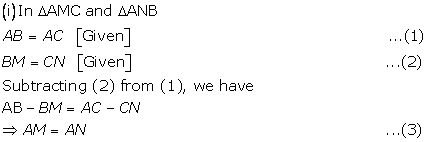



Solution 13

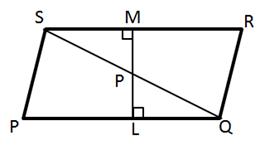
Solution 14

Solution 15

Triangles [Congruency in Triangles] Exercise Test Yourself
Solution 1
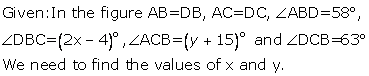

Solution 2
_SHR_files/20140924134305_image003.gif)
Solution 3
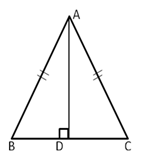

Solution 4

Solution 5

Solution 6

Solution 7
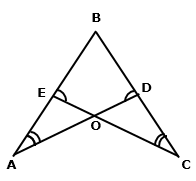
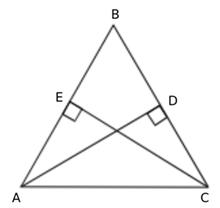
In triangles AOE and COD,
∠A = ∠C (given)
∠AOE = ∠COD (vertically opposite angles)
∴ ∠A + ∠AOE = ∠C + ∠COD
⇒180° - ∠AEO = 180° - ∠CDO
⇒ ∠AEO = ∠ CDO ….(i)
Now, ∠AEO + ∠OEB = 180° (linear pair)
And, ∠CDO + ∠ODB = 180° (linear pair)
∴ ∠AEO + ∠OEB = ∠CDO + ∠ODB
⇒ ∠OEB = ∠ODB [Using (i)]
⇒ ∠CEB = ∠ADB ….(ii)
Now, in ΔABD and ΔCBE,
∠A = ∠C (given)
∠ADB = ∠CEB [From (ii)]
AB = BC (given)
⇒ ΔABD ≅ ΔCBE (by AAS congruence criterion)
Solution 8
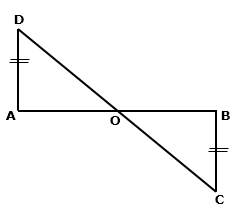
In ΔAOD and ΔBOC,
∠ AOD = ∠ BOC (vertically opposite angles)
∠ DAO = ∠ CBO (each 90°)
AD = BC (given)
∴ ΔAOD ≅ ΔBOC (by AAS congruence criterion)
⇒ AO = BO [cpct]
⇒ O is the mid-point of AB.
Hence, CD bisects AB.
Solution 9
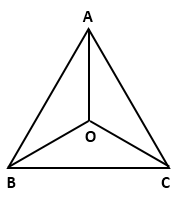
In ΔABC,
AB = AC
⇒ ∠B = ∠C (angles opposite to equal sides are equal)

Solution 10
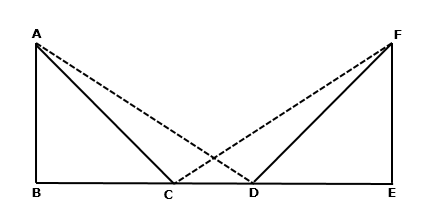
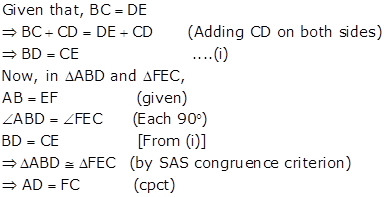
Solution 11
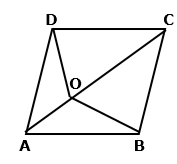
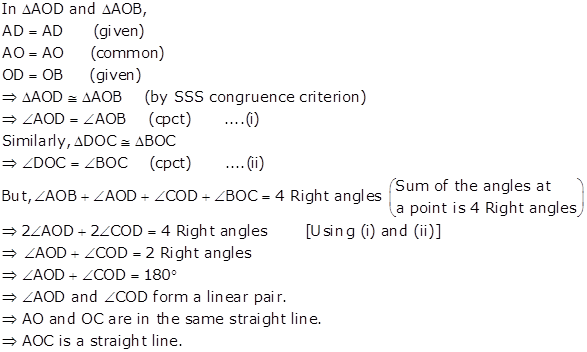
Solution 12
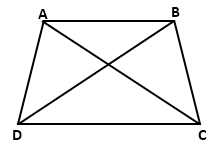
In ΔABD and ΔBAC,
AD = BC (given)
BD = CA (given)
AB = AB (common)
∴ ΔABD ≅ ΔBAC (by SSS congruence criterion)
⇒ ∠ADB = ∠BCA and ∠DAB = ∠CBA (cpct)

