Class 9 SELINA Solutions Maths Chapter 21 - Solids [Surface Area and Volume of 3-D Solids]
Selina Solutions forICSE Class 9 Math is a great source that delivers completely structured support to the students who are preparing for their examinations. Here is how Selina Solutions proves to serve your ultimate partner that helps you devote your valuable time to mastering the chapter "Solid Surface Area and Volume of 3D Solids" for theICSE syllabus.
Why Choose Selina Solutions?
This guide aims to improve exam preparation and comprehension through a range of solutions in the following ways:
- There are step-by-step instructions for surface area and volume estimates while simplifying complex 3D solid principles.
- The solutions successfully explain the real-world illustrations of surface area and volume ideas by intertwining theory with practical familiarity.
- Visual representations like diagrams and 3D models are used, thus, helping students visualise solid 3-D shapes and understand spatial relationships and volumes as well.
- The solutions offer detailed explanations of the formulas used to calculate different solids' surface area and volume. This helps students confidently apply these formulas to various shapes, including cylinders, spheres, cubes, and cones.
- Selina Solutions thoroughly reviews the chapter's fundamental ideas, making them an invaluable exam preparation tool. With the knowledge obtained from these solutions, students can confidently approach exam questions.
Selina Solutions for the Class 9 ICSE chapter "Solid Surface Area and Volume of 3D Solids" is essential for Class 9 students. It is a useful tool for learning and practising solid surface area and volume calculations. Saving time and effort, students may access a variety of knowledge in one location. These solutions give students the tools to understand the challenging calculations involved in determining the surface areas and volumes of various 3-D figures through thorough explanations and engaging tasks.
Selina Solutions offers useful methods for calculating values, encouraging critical thought, and using mathematical ideas in practical contexts. Other study materials are also available to aid students in exam preparations, includingsample papers,video lessons,MCQs, etc.
Solids [Surface Area and Volume of 3-D Solids] Exercise Ex. 21
Solution 1(a)
Correct option: (ii) 4 cm
Let the edge of the cube = 'a' cm
Then, length of the
diagonal![]()
Therefore,
Area of a square on
the diagonal of a cube![]()
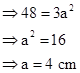
Solution 1(b)
Correct option: (iii) 144 cm2
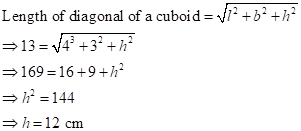
Therefore, volume
of a cuboid = ![]()
= 4 × 3 × 12
= 144 cm3
* Given length, breadth and diagonal of a cuboid, volume of cube cannot be determined.
Solution 1(c)
Correct option: (i) 6 cm
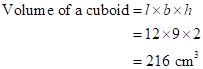
Let the edge of a cube = 'a' cm
Now,
Volume of a cube = Volume of a cuboid
![]()
Solution 1(d)
Correct option: (iv) 18 cm, 12 cm and 12 cm
Let the dimensions of the cuboid be as follows:
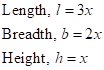
Then,
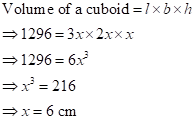
Therefore,
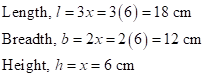
Solution 1(e)
Correct option: (iii) 75 cm
![]()
![]()
Now,
Volume of the soil spread = Area of the field × Rise in level of field
⇒ 960 m3 = 1280 × Rise in level of field
⇒ Rise in level of field = 0.75 m = 75 cm
Solution 1(f)
Correct option: (i) 0.0144 m3
Volume of water flowing in 1 second = 12 × 20 cm3 = 240 cm3
Therefore,
Volume of water flowing in 1 minute = 240 × 60 cm3 = 14,400 cm3 = 0.0144 m3
Solution 1(g)
Correct option: (iv)
![]()
Volume of given solid = Area of cross-section × length
= Area of trapezium × length
![]()
Solution 2
The length, breadth and height of a rectangular solid are in the ratio 5: 4: 2.
Let the length, breadth and height of a cuboid be 5x, 4x and 2x.
Total surface area of a Cuboid = 1216 cm3
⟹ 2(lb + bh + lh) = 1216
⟹ 2(20x2 + 8x2 + 10x2) = 1216
⟹ 76x2 = 1216
⟹ x2 = 16
⟹ x = 4
Therefore, length = 5(4) = 20cm, breadth = 4(4) = 16cm and height = 2(4) = 8cm.
Solution 3
Let a be the one edge of a cube.
Volume![]()
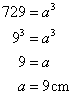
Total surface area=6![]()
Solution 4
Volume of cinema hall![]()
150 ![]() requires= 1 person
requires= 1 person
90000![]() requires=
requires=![]() persons
persons
Therefore, 600 persons can sit in the hall.
Solution 5
Let h be height of the room.
1 person requires 16![]()
75 person requires ![]()
Volume of room is 1200![]()
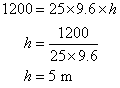
Solution 6
Volume of melted single cube ![]()
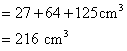
Let a be the edge of the new cube.
Volume![]()
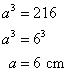
Therefore, 6 cm is the edge of cube.
Solution 7
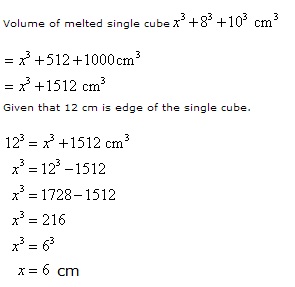
Solution 8
Let the side of a cube be 'a' units.
Total surface area of one cube![]()
Total surface area of 3 cubes ![]()
After joining 3 cubes in a row, length of Cuboid =3a
Breadth and height of cuboid = a
Total surface area of cuboid ![]()
Ratio of total surface area of cuboid to the total surface area of 3 cubes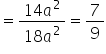
Solution 9

Solution 10
The area of the playground is 3650 m2 and the gravels are 1.2 cm deep. Therefore the total volume to be covered will be:
3650 x 0.012 =43.8 m3.
Since the cost of per cubic meter is Rs. 6.40, therefore the total cost will be:
43.8 x Rs.6.40 = Rs.280.32
Solution 11
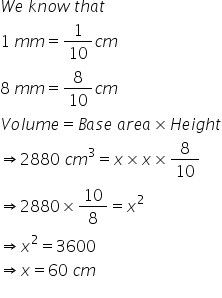
Solution 12
External volume of the box=![]()
Since, external dimensions are 27 cm, 19 cm, 11 cm; thickness of the wood is 1.5 cm.
![]() Internal dimensions
Internal dimensions

Hence, internal volume of box=![]()
(i)
Volume of wood in the box=![]()
(ii)
Cost of wood![]()
![]()
(iii)
Vol. of 4 cm cube=![]()
Number of 4 cm cubes that could be placed into the box
![]()
Solution 13
Area of sheet= Surface area of the tank
![]() Length of the sheet
Length of the sheet![]() its width=Area of 4 walls of the tank +Area of its base
its width=Area of 4 walls of the tank +Area of its base
![]() Length of the sheet
Length of the sheet ![]() 2.5 m=
2.5 m=![]()
![]() Length of the sheet= 300.8 m
Length of the sheet= 300.8 m
Cost of the sheet = 300.8 ![]() Rs 12.50 = Rs 3760
Rs 12.50 = Rs 3760
Solution 14
Let exterior height is h cm. Then interior dimensions are 78-3=75, 19-3=16 and h-3 (subtract two thicknesses of wood). Interior volume = 75 x 16 x (h-3) which must = 15 cu dm
= 15000 cm^3
(1 dm = 10cm, 1 cu dm = 10^3 cm^3).
15000![]() = 75 x 16 x (h-3)
= 75 x 16 x (h-3)
![]() h-3 = 15000/(75x16) = 12.5 cm
h-3 = 15000/(75x16) = 12.5 cm ![]() h = 15.5 cm.
h = 15.5 cm.
Solution 15
(i)
If the side of the cube= a cm
The length of its diagonal= ![]() cm
cm
And,
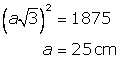
(ii)
Total surface area of the cube=![]()
=![]()
Solution 16
The given figure can be divided into two cuboids of dimensions 6 cm, 4 cm,3 cm, and 9 cm respectively. Hence, volume of solid

Solution 17
Area of cross section of the solid![]()
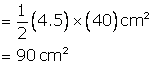
Volume of solid![]()
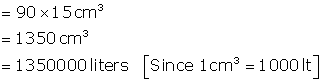
Solution 18
The cross section of a tunnel is of the trapezium shaped ABCD in which ![]() and AM = BN. The height is 2.4 m and its length is 40m.
and AM = BN. The height is 2.4 m and its length is 40m.
(i)
![]()
![]()

Perimeter of the cross- section of the tunnel=![]()
Length=40 m
![]() Internal surface area of the tunnel(except floor)
Internal surface area of the tunnel(except floor)
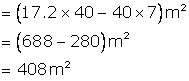
Rate of painting=Rs 5 per![]()
Hence, total cost of painting=Rs 5![]() 408=Rs 2040
408=Rs 2040
(ii)
Area of floor of tunnel![]()
Rate of cost of paving![]()
Total cost=![]()
Solution 19
(i)
The rate of speed ![]()
Volume of water flowing per sec![]()
(ii)
Vol. of water flowing per min![]()
Since 1000![]() = 1 lt
= 1 lt
Therefore, Vol. of water flowing per min=![]()
Solution 20
Vol. of water flowing in 1 sec=![]()
Vol. of water flowing =area of cross section![]() speed of water
speed of water
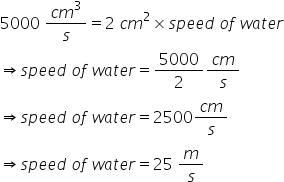
Solution 21
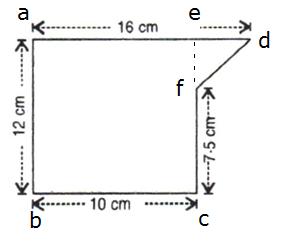
(i)
Area of total cross section= Area of rectangle abce+ area of ![]()
=![]()

(ii)
The volume of the piece of metal in cubic centimeters= Area of total cross section![]()
=![]()
1 cubic centimetre of the metal weighs 6.6 g
![]() of the metal weighs
of the metal weighs![]()
![]()
The weight of the piece of metal to the nearest Kg is 352 Kg.
Solution 22
Vol. of rectangular tank![]()
One liter= 1000![]()
Vol. of water flowing in per sec=
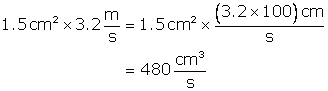
Vol. of water flowing in 1 min=![]()
Hence,
![]() can be filled = 1 min
can be filled = 1 min
![]() can be filled
can be filled![]()
Solids [Surface Area and Volume of 3-D Solids] Exercise Test Yourself
Solution 1
Given that the volume of the iron in the tube 192 cm3
Let the thickness of the tube![]()
![]() Side of the external square=
Side of the external square=![]()
![]() Ext. vol. of the tube
Ext. vol. of the tube ![]() its internal vol.= volume of iron in the tube, we have,
its internal vol.= volume of iron in the tube, we have,

Therefore, thickness is 1 cm.
Solution 2
Let l be the length of the edge of each cube.
The length of the resulting cuboid=![]()
Let width (b) = l cm and its height (h)= l cm
![]() The total surface area of the resulting cuboid
The total surface area of the resulting cuboid
![]()

Therefore, the length of each cube is 6 cm.

Solution 3
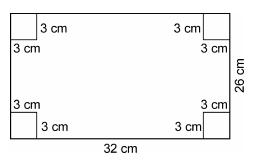
Length of sheet=32 cm
Breadth of sheet=26 cm
Side of each square=3cm
![]() Inner length=32-2
Inner length=32-2![]() 3=32-6=26 cm
3=32-6=26 cm
Inner breadth=![]() cm
cm
By folding the sheet, the length of the container=26 cm
Breadth of the container= 20 cm and height of the container= 3 cm
![]() Vol. of the container=
Vol. of the container=![]()
=![]()
Solution 4
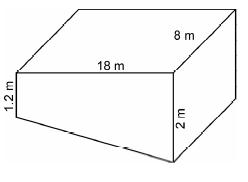
Length of pool= 18 m
Breadth of pool= 8 m
Height of one side= 2m
Height on second side=1.2 m
![]() Volume of pool=
Volume of pool=![]()
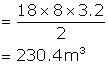
Solution 5
Consider the box 1
_SHR_files/20141014183308_image004.jpg)
Thus, the dimensions of box 1 are: 60 cm, 40 cm and 30 cm.
_SHR_files/20141014183308_image006.png)
Consider the box 2
_SHR_files/20141014183308_image008.jpg)
Thus, the dimensions of box 2 are: 40 cm, 30 cm and 30 cm.
_SHR_files/20141014183308_image010.png)
Consider the box 3
_SHR_files/20141014183308_image012.jpg)
Thus, the dimensions of box 2 are: 40 cm, 30 cm and 20 cm.
_SHR_files/20141014183308_image014.png)
_SHR_files/20141014183308_image016.png)
Solution 6
The perimeter of a cube formula is, Perimeter = 4a where (a= length)
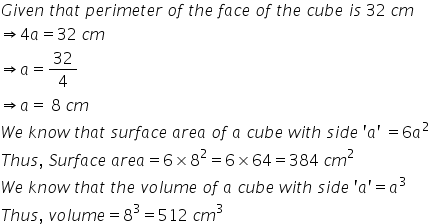
Solution 7
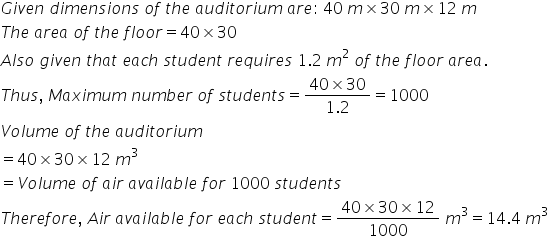
Solution 8
Length of longest rod=Length of the diagonal of the box
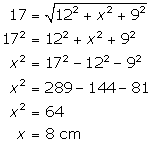
Solution 9
(i)
No. of cube which can be placed along length![]() .
.
No. of cube along the breadth![]()
No. of cubes along the height![]() .
.
![]() The total no. of cubes placed
The total no. of cubes placed![]()
(ii)
Cubes along length![]()
Cubes along width![]() and cubes along height
and cubes along height![]()
![]() The total no. of cubes placed
The total no. of cubes placed![]()
(iii)
Cubes along length![]()
Cubes along width![]() and cubes along height
and cubes along height![]()
![]() The total no. of cubes placed
The total no. of cubes placed![]()
Solution 10
Vol. of the tank= vol. of earth spread

Solution 11
_SHR_files/20141015093546_image002.png)
Solution 12
_SHR_files/20141015093546_image004.png)
_SHR_files/20141015093546_image006.jpg)
_SHR_files/20141015093546_image008.png)
Solution 13
_SHR_files/20141015093546_image016.png)
Solution 14
_SHR_files/20141015093546_image018.png)
Solution 15
_SHR_files/20141015093546_image024.png)

