Class 9 SELINA Solutions Maths Chapter 19 - Mean and Median (For Ungrouped Data Only)
Mean and Median (For Ungrouped Data Only) Exercise Ex. 19(A)
Solution 1(a)
Correct option: (i) ![]()
Number of observations = 4
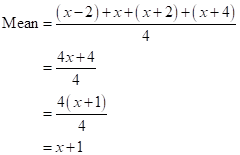 .
.
Solution 1(b)
Correct option: (ii) 31
Mean of 10 observations = 20
∴ Sum of 10 observations = 20 × 10 = 200
On including one observation, the mean of 11 observations = 21
∴ Sum of 11 observations = 21 × 11 = 231
Hence, included number
= Sum of 11 observations - Sum of 10 observations
= 231 - 200
= 31
Solution 1(c)
Correct option: (iii) 68
Mean of 20 observations = 30
∴ Sum of 20 observations = 30 × 20 = 600
On excluding one observation, the mean of remaining 19 observations = 28
∴ Sum of remaining 19 observations = 28 × 19 = 532
Hence, excluded number
= Sum of 20 observations - Sum of 19 observations
= 600 - 532
= 68
Solution 1(d)
Correct option: (iii) is decreased by 15
If each observation in a data set is decreased by quantity 'a', then their mean is also decreased by the same quantity 'a'.
Hence, if each observation of the data is decreased by 15, then the mean is decreased by 15.
Solution 1(e)
Correct option: (iv) 23
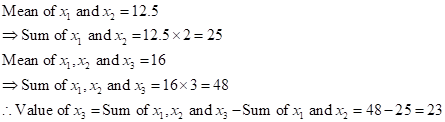
Solution 2
The numbers given are ![]()
The mean of the given numbers will be
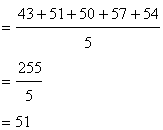
Solution 3
The first six natural numbers are ![]()
The mean of first six natural numbers
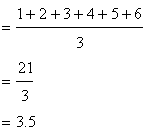
Solution 4
The first ten odd natural numbers are ![]()
The mean of first ten odd numbers
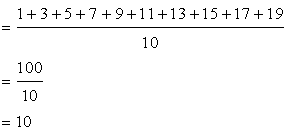
Solution 5
The all factors of 10are ![]()
The mean of all factors of 10 are
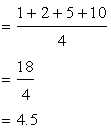
Solution 6
The given values are ![]()
The mean of the values are

Solution 7
(i)The given numbers are![]()
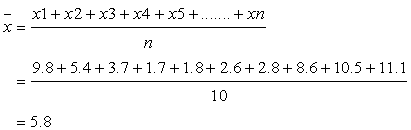
(ii) The value of ![]()
We know that
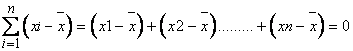
Here
![]()
Therefore
![]()

![]()
![]()
Solution 8
Given that the mean of 15 observations is 32
(i)resulting mean increased by 3
=32 + 3
=35
(ii)resulting mean decreased by 7
=32 - 7
= 25
(iii)resulting mean multiplied by 2
=32*2
=64
(iv)resulting mean divide by 0.5
![]()
(v)resulting mean increased by 60%
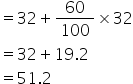
(vi)resulting mean decreased by 20%
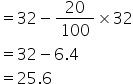
Solution 9
Given the mean of 5 numbers is 18
Total sum of 5 numbers
=18*5
=90
On excluding an observation, the mean of remaining 4 observation is 16
=16*4
=64
Therefore sum of remaining 4 observations
![]() total of 5 observations-total of 4 observations
total of 5 observations-total of 4 observations
= 90 - 64
= 26
Solution 10
(i)Given that the mean of observations x, x + 2, x + 4, x + 6 and x + 8 is 11
Mean=![]()

(ii)The mean of first three observations are
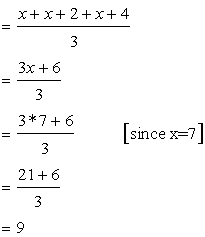
Mean and Median (For Ungrouped Data Only) Exercise Ex. 19(B)
Solution 1(a)
Correct option: (iii) 0
Median is the value of the middle observation when data is arranged either in ascending or descending order.
Hence, median is not affected by extreme values.
So, if the last observation is doubled, the median will increase by 0.
Solution 1(b)
Correct option: (i) remain same
Median is the value of the middle observation when data is arranged either in ascending or descending order.
Hence, median is not affected by extreme values.
So, if the first observation is doubled, the median will remain same.
Solution 1(c)
Correct option: (ii) 10
Number of observations, n = 9 (odd)
Arranging data in ascending order:
4, 6, 8, 9, 10, 10, 10, 12, 12
Therefore,
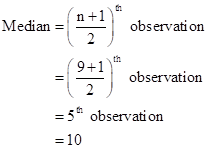
Solution 1(d)
Correct option: (iv) 120
Median is the value of the middle observation when data is arranged either in ascending or descending order.
Then, if each observation is doubled, the middle value will be doubled and hence the median will also be doubled.
So, the resulting median will be 60 × 2 = 120.
Solution 1(e)
Correct option: (iii) mean and median both decrease by 2
If each observation in a data set is decreased by quantity '2', then their mean is also decreased by the same quantity '2'.
Since median is the value of the middle observation when data is arranged either in ascending or descending order, if each observation is decreased by 2, the middle value will decrease by 2 and hence the median will also decrease by 2.
Solution 2
(i)Firstly arrange the numbers in ascending order
![]()
Now since
n=9(odd)
Therefore Median

Thus the median is ![]()
(ii)
Firstly arrange the numbers in ascending order
241, 243, 257, 258, 261, 271, 292, 299, 327, 347, 350
Now since n=11(Odd)

(iii) Firstly arrange the numbers in ascending order
![]()
Now since n=10(even)
![]()

Thus the median is ![]()
(iv) Firstly arrange the numbers in ascending order
173,185,189,194,194,200,204,208,220,223

Thus the median is 197
Solution 3
Given numbers are 34, 37, 53, 55, x, x+2, 77, 83, 89, 100
Here n = 10(even)

Solution 4
For any given set of data, the median is the value of its middle term.
Here, total observations = n = 10 (even)
If n is even, we have

Thus, for n = 10, we have
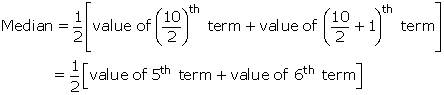
Hence, if 7th number is increased by 8, there is no change in the median value.
Solution 5
Here, total observations = n = 10 (even)
Thus, we have
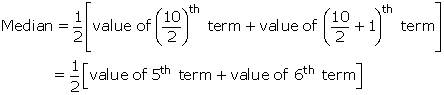
According to given information, data in ascending order is as follows:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Marks |
Less than 30 |
35 |
40 |
48 |
66 |
More than 75 |
||||
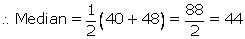
Hence, the median score of the whole group is 44.
Solution 6

Mean and Median (For Ungrouped Data Only) Exercise Test Yourself
Solution 1
Given the mean of 100 observations is 40.

Incorrect value of x=4000
Correct value of x=Incorrect value of x-Incorrect observation + correct observation
=4000-83+53
=3970
Correct mean

Solution 2
Given that the mean of 200 items was 50.

Incorrect value of ![]()
Correct value of

Correct mean

Solution 3
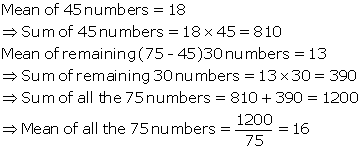
Solution 4

Solution 5

Solution 6

Solution 7
Total number of tests = 8
Average score of A = 25
Let the score of 8th test be x.
Then, total score of 8 tests = 29 + 26 + 18 + 20 + 27 + 24 + 29 + x
Now, we have

Thus, A scored 27 marks in the eight test.
Solution 8
_SHR_files/20140926172740_image002.gif)
(i) Multiplied by 3
_SHR_files/20140926172740_image004.gif)
(ii) Divided by 2
_SHR_files/20140926172740_image006.gif)
(iii) multiplied by 3 and then divided by 2
_SHR_files/20140926172740_image008.gif)
(iv) increased by 25%
_SHR_files/20140926172740_image010.gif)
(v) decreased by 40%
_SHR_files/20140926172740_image012.gif)
Solution 9
_SHR_files/20140926172740_image014.gif)
Solution 10
_SHR_files/20140926172740_image016.gif)
Solution 11
_SHR_files/20140926172740_image018.gif)
Solution 12
_SHR_files/20140926172740_image020.gif)
Solution 13
_SHR_files/20140926172740_image022.gif)
Solution 14
_SHR_files/20140926172740_image024.gif)
(i) Let us tabulate the observations and their deviations from the mean
_SHR_files/20140926172740_image026.gif)
(ii)
_SHR_files/20140926172740_image028.gif)
Solution 15
_SHR_files/20140926172740_image030.gif)
Let us rewrite the given data in ascending order:
Thus, we have
35, 48, 51, 52, 63, 64, 71, 76, 92
There are 9 observations, which is odd.
_SHR_files/20140926172740_image032.gif)
If 51 is replaced by 66, the new set of data in ascending order is:
35, 48, 52, 63, 64, 66, 71, 76, 92
![]()
Solution 16
_SHR_files/20140926172740_image036.gif)
Solution 17
_SHR_files/20140926172740_image038.gif)
Therefore, the data set is:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
_SHR_files/20140926172740_image040.gif)
Solution 18
Total number of students = 60
Mean weight of 60 students = 40
Let the number of boys = x
Then, number of girls = 60 - x
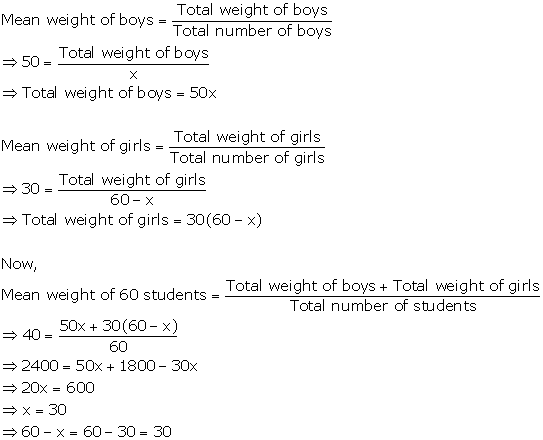
Hence, the number of boys is 30 and the number of girls is also 30.
Solution 19
Mean of n numbers = A
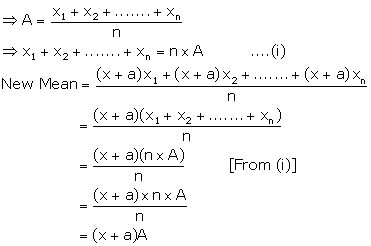
Solution 20
Total number of players in each team = 7

Thus, team A has greater average height.
Median of team A:
Arranging heights in ascending order, we get
175, 176, 178, 180, 181, 187, 190
Total number of observations = n = 7 (odd)
![]()
Median of team B:
Arranging heights in ascending order, we get
174, 175, 177, 178, 179, 185, 190
Total number of observations = n = 7 (odd)
![]()

