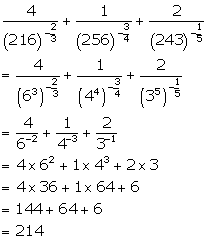Class 9 SELINA Solutions Maths Chapter 7 - Indices (Exponents)
Ex. 7(A)
Ex. 7(B)
Test Yourself
Indices (Exponents) Exercise Ex. 7(A)
Solution 1(a)
Correct option:
(ii) ![]()
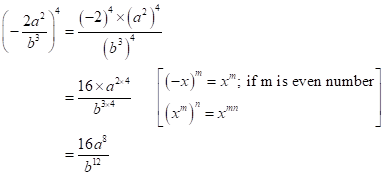
Solution 1(b)
Correct option: (i) ![]()

Solution 1(c)
Correct option:
(iii) ![]()
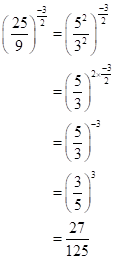
Solution 1(d)
Correct option: (iv) 6
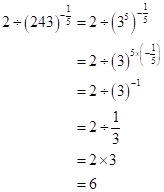
Solution 1(e)
Correct option: (i) 10
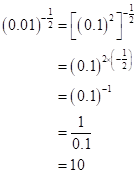
Solution 1(f)
Correct option: (ii) 12

Solution 2
(i)

(ii)

(iii)
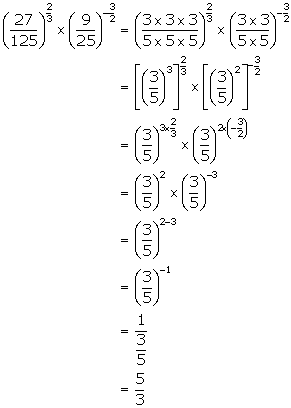
(iv)

(v)
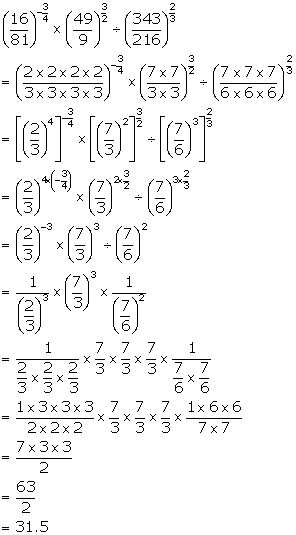
Solution 3
(i)
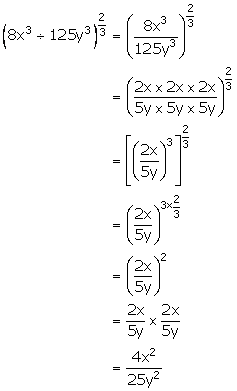
(ii)

(iii)

(iv)

Solution 4
(i)

(ii)
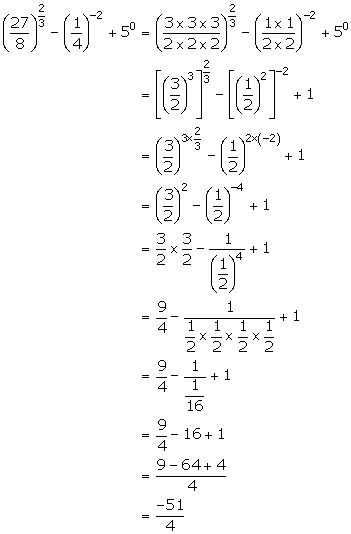
Solution 5
(i)

(ii)

(iii)
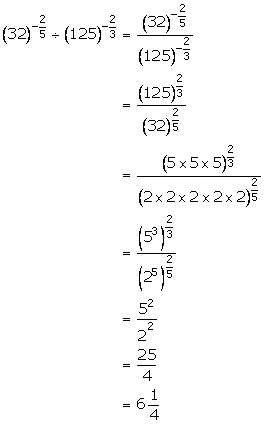
(iv)

Solution 6
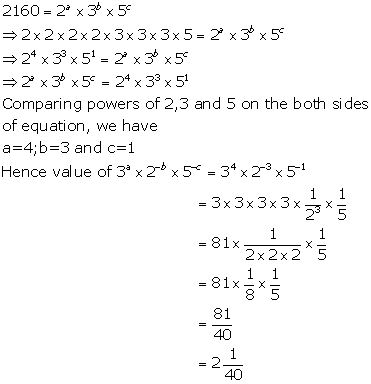
Solution 7
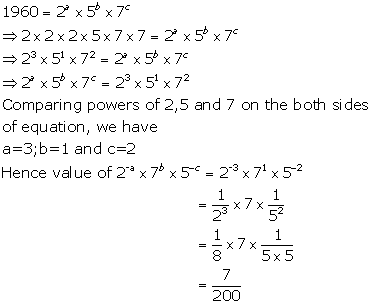
Solution 8
(i)

(ii)

Solution 9

Solution 10
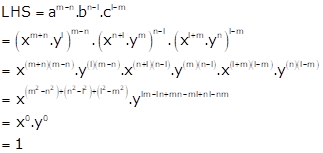
Solution 11
(i)

(ii)

Indices (Exponents) Exercise Ex. 7(B)
Solution 1(a)
Correct option: (i) ![]()
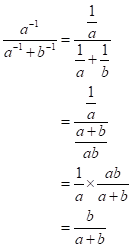
Solution 1(b)
Correct option:
(ii) ![]()
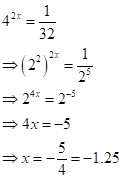
Solution 1(c)
Correct option:
(iii) ![]()

Solution 1(d)
Correct option: (i) ![]()
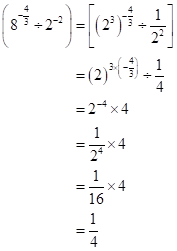
Solution 1(e)
Correct option: (i) ![]()
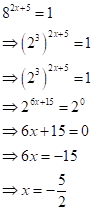
Solution 1(f)
Correct option: (ii) 5
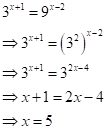
Solution 1(g)
Correct option: (i) ![]()
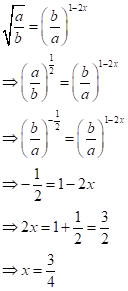
Solution 2
(i)
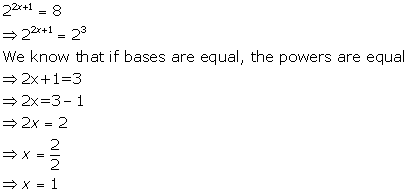
(ii)

(iii)

(iv)

Solution 3
(i)
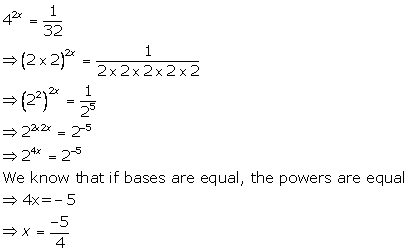
(ii)
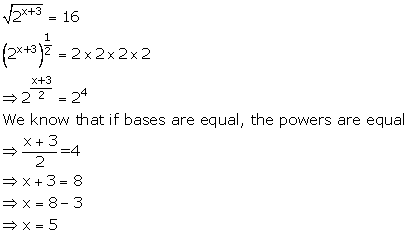
(iii)
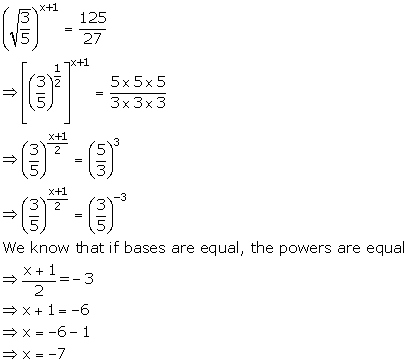
(iv)
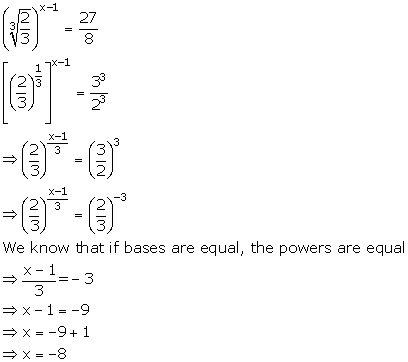
Solution 4
(i)

(ii)

Solution 5
(i)

(ii)

(iii)

Solution 6

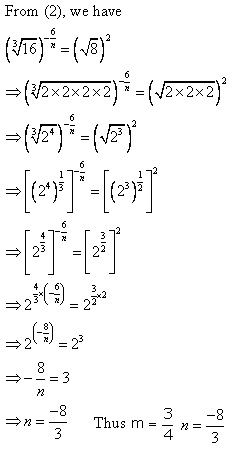
Solution 7


Solution 8
(i)

(ii)
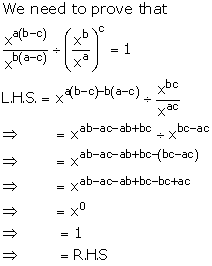
Solution 9

Solution 10
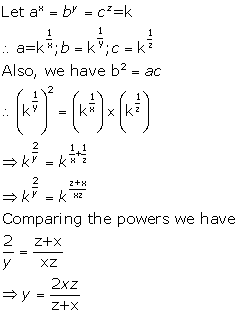
Solution 11
_SHR_files/20140923150850_image004.gif)
Solution 12
_SHR_files/20140923150850_image006.gif)
Solution 13
_SHR_files/20140923150850_image008.gif)
Solution 14
_SHR_files/20140923150850_image010.gif)
Solution 15 (i)
_SHR_files/20140923150850_image014.gif)
Solution 15 (ii)
_SHR_files/20140923150850_image016.gif)
Solution 15 (iii)
_SHR_files/20140923150850_image020.gif)
Solution 15 (iv)
_SHR_files/20140923150850_image022.gif)
Solution 15 (v)
_SHR_files/20140923150850_image024.gif)
Solution 15 (vi)
9x+2 = 720 + 9x
⇒ 9x+2 - 9x = 720
⇒ 9x (92 - 1) = 720
⇒ 9x (81 - 1) = 720
⇒ 9x (80) = 720
⇒ 9x = 9
⇒ 9x = 91
⇒ x = 1
Indices (Exponents) Exercise Test Yourself
Solution 1

Solution 2

Solution 3
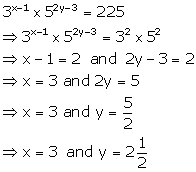
Solution 4
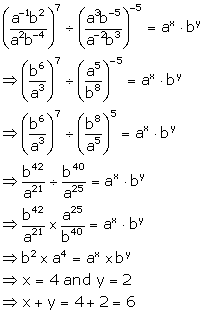
Solution 5

Solution 6
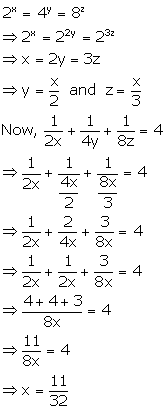
Solution 7

Solution 8

Solution 9

Solution 10
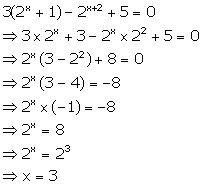
Solution 11
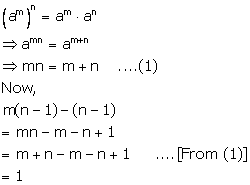
Solution 12
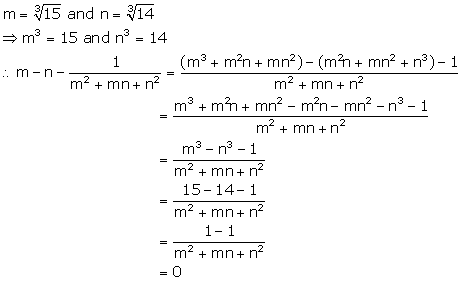
Solution 13
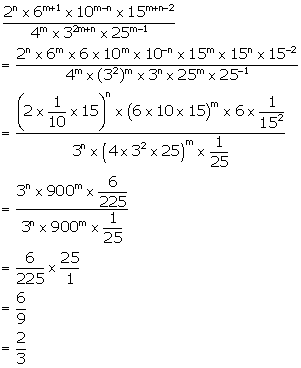
Solution 14
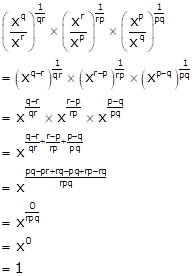
Solution 15 (i)
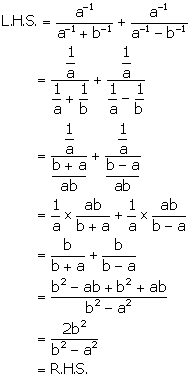
Solution 15 (ii)
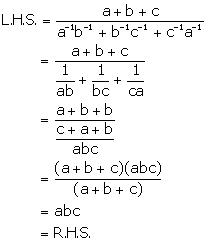
Solution 16