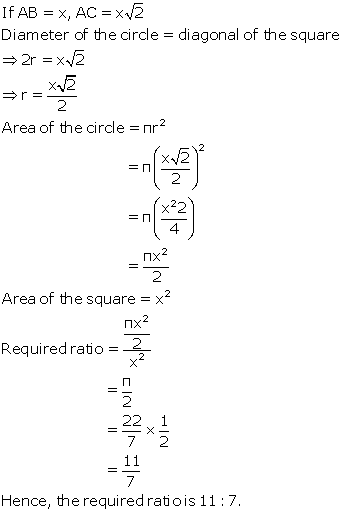Class 9 SELINA Solutions Maths Chapter 20 - Area and Perimeter of Plane Figures
Area and Perimeter of Plane Figures Exercise Ex. 20(A)
Solution 1(a)
Correct option: (iii) four times
![]()
If length and corresponding altitude is doubled, then
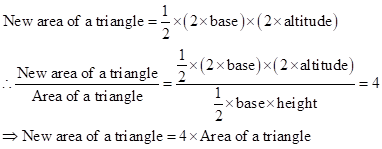
Solution 1(b)
Correct option: (iv) one-fourth
![]()
If each side is halved, then
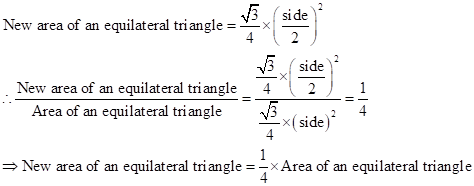
Solution 1(c)
Correct option: (iii) 6 cm
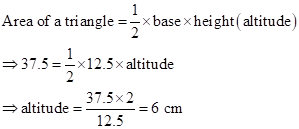
Solution 1(d)
Correct option: (iii) 72 cm2
The area of a right-angled triangle is equal to half the product of the sides containing the right angle.
Therefore,
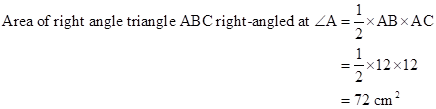
Solution 1(e)
Correct option: (i) 54 cm2
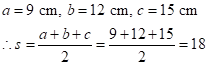
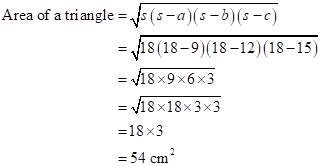
Solution 2
Since the sides of the triangle are 18cm,24cm and 30cm respectively.
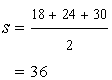
Hence area of the triangle is

Again
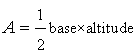
Hence
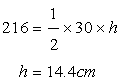
Solution 3
Let the sides of the triangle are
a=3x
b=4x
c=5x
Given that the perimeter is 144 cm.
hence
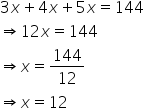
![]()
The sides are a=36 cm, b=48 cm and c=60 cm
Area of the triangle is![]()
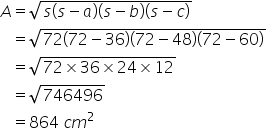
Solution 4
(i)
Area of the triangle is given by
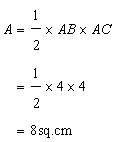
(ii)
Again area of the triangle

Solution 5
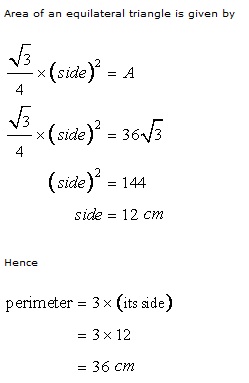
Solution 6
Since the perimeter of the isosceles triangle is 36cm and base is 16cm. hence the length of each of equal sides are 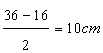
Here
It is given that
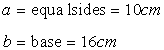
Let 'h' be the altitude of the isosceles triangle.
Since the altitude from the vertex bisects the base perpendicularly, we can apply Pythagoras Theorem.
Thus we have,
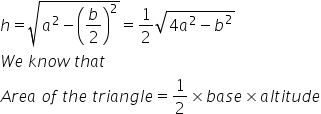
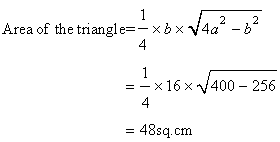
Solution 7
It is given that
![]()

Let 'a' be the length of an equal side.
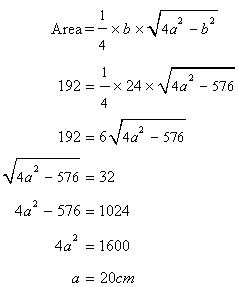
Hence perimeter=![]()
Solution 8
From ![]() ,
,

Area of![]()
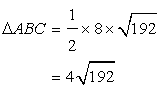
Area of ![]()
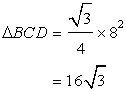
Now
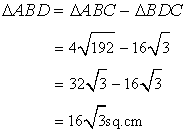
Solution 9
Given , AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ![]() DBC = 90o
DBC = 90o
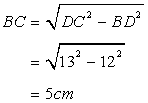
Hence perimeter=8+10+13+5=36cm
Area of ![]()

Area of ![]()
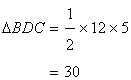
Now
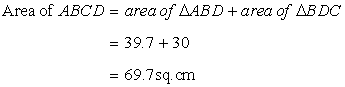
Solution 10

Solution 11
(i)
_SHR_files/20141020195131_image002.gif)
(ii) Consider the following figure.
_SHR_files/20141020195131_image003.jpg)
_SHR_files/20141020195131_image005.gif)
_SHR_files/20141020195131_image007.gif)
_SHR_files/20141020195131_image009.gif)
(iii)
_SHR_files/20141020195131_image011.gif)
Solution 12
Let the height of the triangle be x cm.
Equal sides are (x+4) cm.
According to Pythagoras theorem,

Hence perimeter=![]()
Area of the isosceles triangle is given by
Here a=20cm
b=24cm
hence
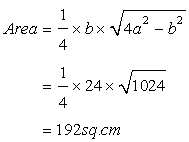
Solution 13
Each side of the triangle is 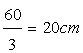
Hence the area of the equilateral triangle is given by
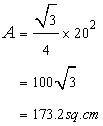
The height h of the triangle is given by
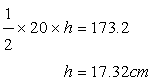
Solution 14
The area of the triangle is given as 150sq.cm
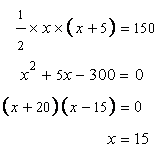
Hence AB=15cm,AC=20cm and
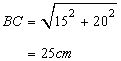
Solution 15
Let the two sides be x cm and (x-3) cm.
Now
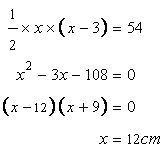
Hence the sides are 12cm, 9cm and ![]()
The required perimeter is 12+9+15=36cm.
Area and Perimeter of Plane Figures Exercise Ex. 20(B)
Solution 1(a)
Correct option: (ii)
![]()
When two diagonals of a quadrilateral cut each other at right angles, then
![]()
Solution 1(b)
Correct option: (i) ![]()
![]()
Solution 1(c)
Correct option: (iii) 256 cm2
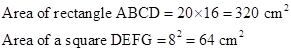
Therefore,
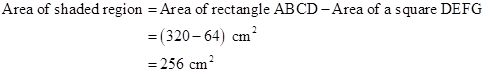
Solution 1(d)
Correct option: (iii) 324 cm2
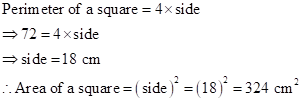
Solution 1(e)
Correct option: (iv) 36 cm
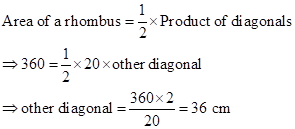
Solution 2

Solution 3

Solution 4
Consider the figure:
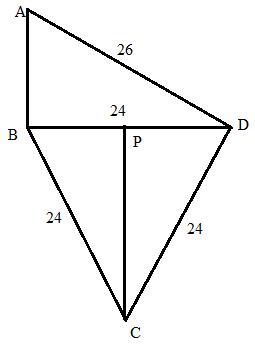
From the right triangle ABD we have

The area of right triangle ABD will be:
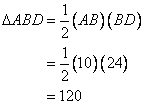
Again from the equilateral triangle BCD we have ![]()
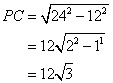
Therefore the area of the triangle BCD will be:
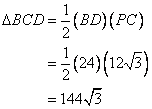
Hence the area of the quadrilateral will be:
![]()
Solution 5
The figure can be drawn as follows:
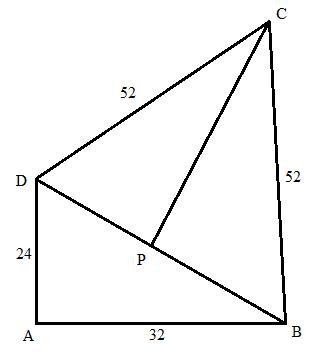
Here ABD is a right triangle. So the area will be:
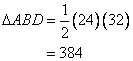
Again

Now BCD is an isosceles triangle and BP is perpendicular to BD, therefore

From the right triangle DPC we have

So
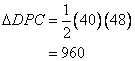
Hence the area of the quadrilateral will be:
![]()
Solution 6
Let the width be x and length 2x km.
Hence

Hence the width is 100m and length is 200m
The required area is given by
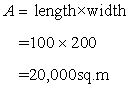
Solution 7
Length of the laid with grass=85-5-5=75m
Width of the laid with grass=60-5-5=50m
Hence area of the laid with grass is given by
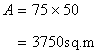
Solution 8
Area of the rectangle is given by
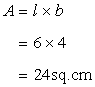
Let h be the height of the triangle ,then
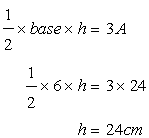
Solution 9
Consider the following figure.
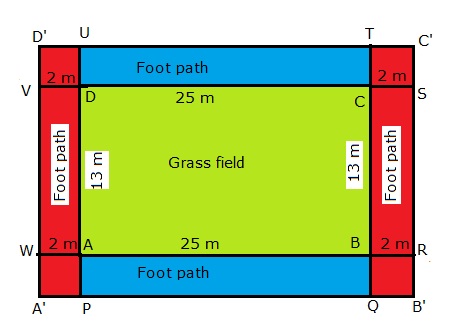
Thus the required area = area shaded in blue + area shaded in red
= Area ABPQ + Area TUDC + Area A'PUD' + Area QB'C'T
= 2Area ABPQ + 2Area QB'C'T
=2(Area ABPQ +Area QB'C'T)

Solution 10
Perimeter of the garden
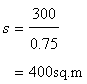
Again, length of the garden is given to be 120 m. hence breadth of the garden b is given by

Hence area of the field
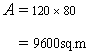
Solution 11
Length of the rectangle=x
Width of the rectangle=![]()
Hence its perimeter is given by

Again it is given that the perimeter is 4400cm.
Hence
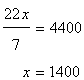
Length of the rectangle=1400 cm = 14 m
Solution 12
(i)
Breadth of the verandah=x
Length of the verandah=x+3
According to the question
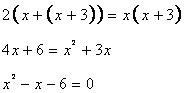
(ii)
From the above equation
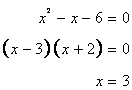
Hence breadth=3m
Length =3+3=6m
Solution 13
Consider the following figure.
_SHR_files/20141014160129_image004.jpg)
Thus, the area of the shaded portion
=Area(ABCD) + Area(EFGH) - Area(IJKL)…(1)
_SHR_files/20141014160129_image006.png)
Solution 14
First we have to calculate the area of the hall.
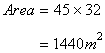
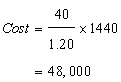
We need to find the cost of carpeting of 80 cm = 0.8 m wide carpet, if the rate of carpeting is Rs. 25. Per metre.
Then
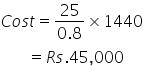
Solution 15
Let a be the length of each side of the square.
Hence

Hence
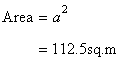
And
![]()
Solution 16
Consider the following figure.
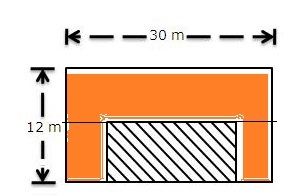
(i)
The length of the lawn = 30 - 2 - 2 = 26 m
The breadth of the lawn = 12 - 2 = 10 m
(ii)
The orange shaded area in the figure is the required area.
Area of the flower bed is calculated as follows:
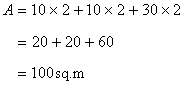
Solution 17
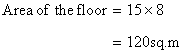
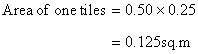
Number of tiles required

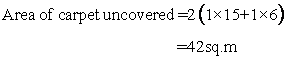
Fraction of floor uncovered=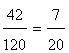
Solution 18
Since
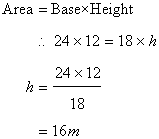
Hence the distance between the shorter sides is 16m.
Solution 19
At first we have to calculate the area of the triangle having sides, 28cm, 26cm and 30cm.
Let the area be S.
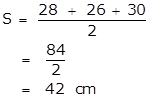
By Heron's Formula,
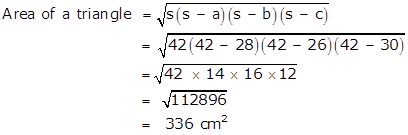
Area of a Parallelogram = 2 × Area of a triangle
= 2 × 336
= 672 cm2
We know that,
Area of a parallelogram = Height × Base
⇒ 672 = Height × 26
⇒ Height = 25.84 cm
∴ the distance between its shorter sides is 25.84 cm.
Solution 20
(i)
We know that
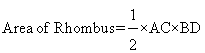
Here A=216sq.cm
AC=24cm
BD=?
Now
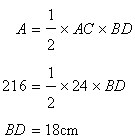
(ii)
Let a be the length of each side of the rhombus.

(iii)
Perimeter of the rhombus=4a=60cm.
Solution 21
Let a be the length of each side of the rhombus.

(i)
It is given that,
AC=24cm
We have to find BD.
Now

Hence the other diagonal is 10cm.
(ii)
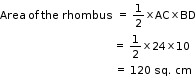
Solution 22
Let a be the length of each side of the rhombus.
![]()

We know that,
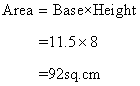
Solution 23
The diagram is redrawn as follows:
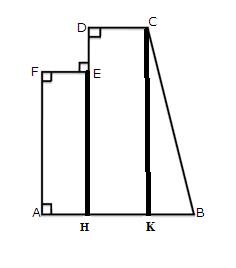
Here
AF=1.2m,EF=0.3m,DC=0.6m,BK=1.8-0.6-0.3=0.9m
Hence
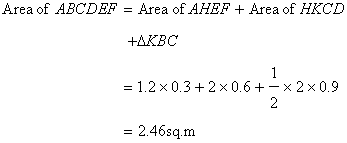
Solution 24
Here we found two geometrical figure, one is a triangle and other is the trapezium.
Now
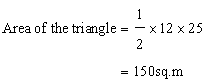

hence area of the whole figure=150+240=630sq.m
Solution 25
We can divide the field into three triangles and one trapezium.
Let A,B,C be the three triangular region and D be the trapezoidal region.
Now

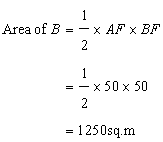
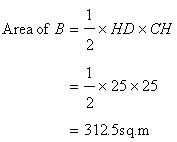

Area of the figure=Area of A+ Area of B+ Area of C+ Area of D
=3900+1250+312.5+2062.5
=7525sq.m
Mean and Median (For Ungrouped Data Only) Exercise Ex. 20(C)
Solution 1(a)
Correct option: (i) 77 cm2
In right-angled ΔABC,
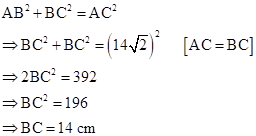
Diameter of semi-circle BPC = BC = 14 cm
⇒ Radius of semi-circle BPC, r = 7 cm
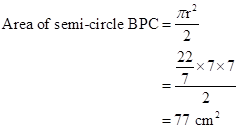
Solution 1(b)
Correct option: (ii) doubled
Diameter of a circle = 14 cm
![]()
If diameter is doubled, then
![]()
Solution 1(c)
Correct option: (iii) 42 cm2
Radius of a quadrant OCA = Side of a square = 14 cm
Then,
![]()
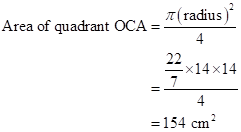
Now, area of shaded portion = Area of square OCBA - Area of quadrant OCA
= (196 - 154) cm2
= 42 cm2
Solution 1(d)
Correct option: (iii) four times
Let the radius of a circle = r
Then, ![]()
If radius is doubled, then
![]()
Solution 1(e)
Correct option: (i) 1848 cm2
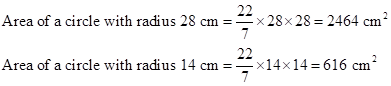
Therefore,
area of shaded portion = Area of circle with radius 28 cm - Area of circle with radius 14 cm
= (2464 - 616) cm2
= 1848 cm2
Solution 2
Let r be the radius of the circle.
(i)
![]()
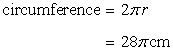
= 88 cm
(ii)

= 616 cm2
Solution 3

Solution 4
Let r be the radius of the circle.

Solution 5
Circumference of the first circle
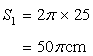
Circumference of the second circle
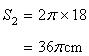
Let r be the radius of the resulting circle.
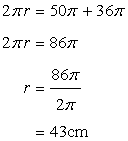
Solution 6
Circumference of the first circle
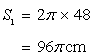
Circumference of the second circle
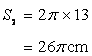
Let r be the radius of the resulting circle.
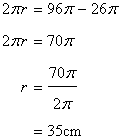
Hencearea of the circle
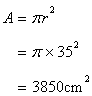
Solution 7
Let the area of the resulting circle be r.
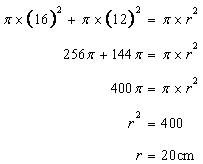
Hence the radius of the resulting circle is 20cm.
Solution 8
Area of the circle having radius 85m is
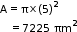
Let r be the radius of the circle whose area is 49times of the given circle.

Hence circumference of the circle
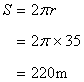
Solution 9
Area of the rectangle is given by
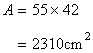
For the largest circle, the radius of the circle will be half of the sorter side of the rectangle.
Hence r=21cm.
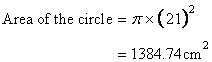
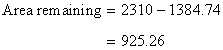
Hence

Solution 10
Area of the square is given by
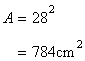
Since there are four identical circlesinside the square.
Hence radius of each circle is one fourth of the side of the square.

Area remaining in the cardboard is ![]()
Solution 11
Let the radius of the two circles be 3r and 8r respectively.

According to the question
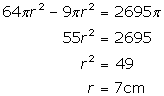
Hence radius of the smaller circle is ![]()
Area of the smaller circle is given by
![]()
Solution 12
Let the diameter of the three circles be 3d, 5d and 6d respectively.
Now
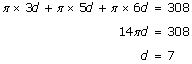
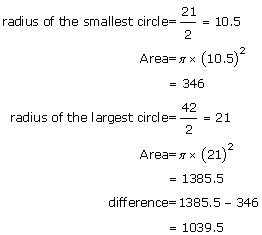
Solution 13

Solution 14
Let r be the radius of the circular park.
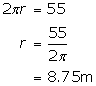
![]()
Radius of the outer circular region including the path is given by
![]()
Area of that circular region is
![]()
Hence area of the path is given by
![]()
Solution 15

Solution 16

Solution 17


Solution 18
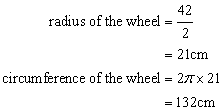

Solution 19
Time interval is ![]()
Area covered in one 60 minutes=![]()
Hence area swept in 35 minutes is given by
![]()
Solution 20
Let R and r be the radius of the big and small circles respectively.

Area and Perimeter of Plane Figures Exercise Test Yourself
Solution 1
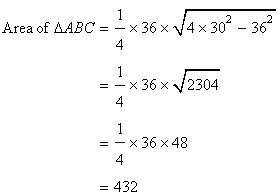
Since AB=AC and ![]()
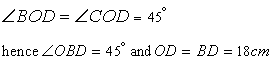
Now
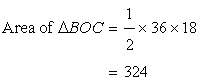

Solution 2
Let x be the width of the footpath.
Then
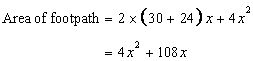
Again it is given that area of the footpath is 360sq.m.
Hence

Hence width of the footpath is 3m.
Solution 3
Area of the square is 484.
Let a be the length of each side of the square.
Now
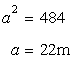
Hence length of the wire is=4x22=88m.
(i)
Now this 88m wire is bent in the form of an equilateral triangle.

(ii)
Let x be the breadth of the rectangle.
Now

Hence area=16x28=448m2
Solution 4
(i)
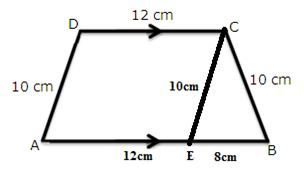

Again
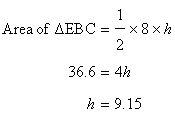

(ii)
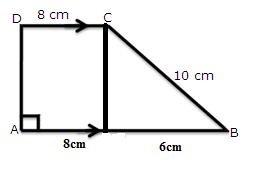

(iii)
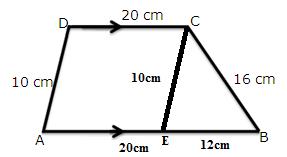
For the triangle EBC,
S=19cm
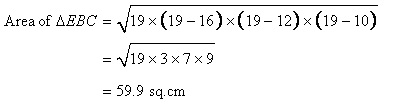
Let h be the height.
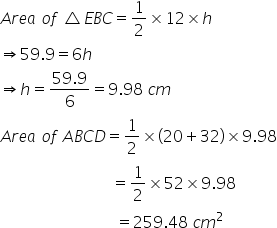
(iv)
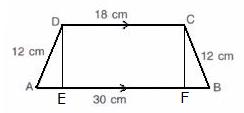
In the given figure, we can observe that the non-parallel sides are equal and hence it is an isosceles trapezium.
Therefore, let us draw DE and CF perpendiculars to AB.
Thus, the area of the parallelogram is given by

Solution 5
Let b be the breadth of rectangle. then its perimeter
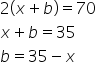
Again

Hence its length is 20cm and width is 15cm.
Solution 6
Let b be the width of the rectangle.
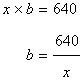
Again perimeter of the rectangle is 104m.
Hence

Hence
length=32m
width=20m.
Solution 7
Let a be the length of the sides of the square.
According to the question

Hence sides of the square are 12cm each and
Length of the rectangle =2a=24cm
Width of the rectangle=a+6=18cm.
Solution 8
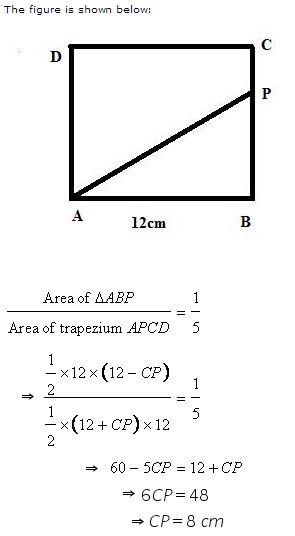
Solution 9
Length of the wall=45+2=47m
Breath of the wall=30+2=32m
Hence area of the inner surface of the wall is given by
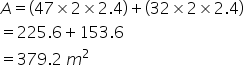
Solution 10
Let a be the length of each side.
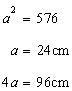
Hence length of the wire=96cm
(i)
For the equilateral triangle,

(ii)
Let the adjacent side of the rectangle be x and y cm.
Since the perimeter is 96 cm, we have,
![]()
Hence
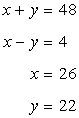
Hence area of the rectangle is = 26 x 22 = 572 sq.cm
Solution 11
Let 'y' and 'h' be the area and the height of the first parallelogram respectively.
Let 'height' be the height of the second parallelogram
base of the first parallelogram=![]() cm
cm
base of second parallelogram= cm
cm

Solution 12

Solution 13

Solution 14
Let the radius of the field is r meter.
Therefore circumference of the field will be: ![]() meter.
meter.
Now the cost of fencing the circular field is 52,800 at rate 240 per meter.
Therefore
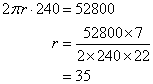
Thus the radius of the field is 35 meter.
Now the area of the field will be:
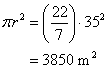
Thus the cost of ploughing the field will be:
![]()
Solution 15
Let r and R be the radius of the two circles.
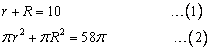
Putting the value of r in (2)

Hence the radius of the two circles is 3cm and 7cm respectively.
Solution 16

Solution 17
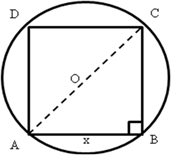
Since the diameter of the circle is the diagonal of the square inscribed in the circle.
Let a be the length of the sides of the square.
Hence
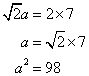
Hence the area of the square is 98sq.cm.![]()
Solution 18

Solution 19
Let the sides of the triangle be
a = 12x
b = 5x
c = 13x
Given that the perimeter = 450 cm
⇒ 12x + 5x + 13x = 450
⇒ 30x = 450
⇒ x = 15
Hence, the sides of a triangle are
a = 12x = 12(15) = 180 cm
b = 5x = 5(15) = 75 cm
c = 13x = 13(15) = 195 cm
Now,
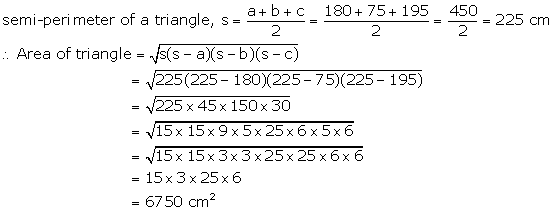
Solution 20
Let the sides of the triangle be
a = 26 cm, b = 28 cm and c = 30 cm
Now,

Solution 21
Construction: Draw CM ⊥ AB
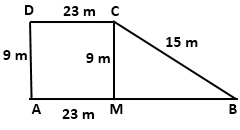
In right-angled triangle CMB,
BM2 = BC2 - CM2 = (15)2 - (9)2 = 225 - 81 = 144
⇒ BM = 12 m
Now, AB = AM + BM = 23 + 12 = 35 m
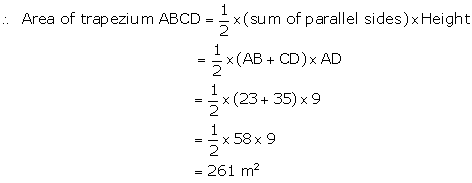
Solution 22
Let the sides of two squares be a and b respectively.
Then, area of one square, S1 = a2
And, area of second square, S2 = b2
Given, S1 + S2 = 400 cm2
⇒ a2 + b2 = 400 cm2 …..(1)
Also, difference in perimeter = 16 cm
⇒ 4a - 4b = 16 cm
⇒ a - b = 4
⇒ a = (4 + b)
Substituting the value of 'a' in (1), we get
(4 + b)2 + b2 = 400
⇒ 16 + 8b + b2 + b2 = 400
⇒ 2b2 + 8b - 384 = 0
⇒ b2 + 4b - 192 = 0
⇒ b2 + 16b - 12b - 192 = 0
⇒ b(b + 16) - 12(b + 16) = 0
⇒ (b +16)(b - 12) = 0
⇒ b + 16 = 0 or b - 12 = 0
⇒ b = -16 or b = 12
Since, the side of a square cannot be negative, we reject -16.
Thus, b = 12
⇒ a = 4 + b = 4 + 12 = 16
Hence, the sides of a square are 16 cm and 12 cm respectively.
Solution 23
Diagonal of a square = 24 cm
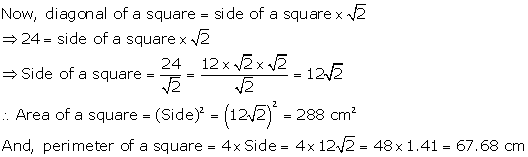
Solution 24

Solution 25

Solution 26
Let the radii of two circles be r1 and r2 respectively.
Sum of the areas of two circles = 130π sq. cm
⇒ πr12 + πr22 = 130π
⇒ r12 + r22 = 130 ….(i)
Also, distance between two radii = 14 cm
⇒ r1 + r2 = 14
⇒ r1 = (14 - r2)
Substituting the value of r1 in (i), we get
(14 - r2)2 + r22 = 130
⇒ 196 - 28r2 + r22 + r22 = 130
⇒ 2r22 - 28r2 + 66 = 0
⇒ r22 - 14r2 + 33 = 0
⇒ r22 - 11r2 - 3r2 + 33 = 0
⇒ r2 (r2 - 11) - 3 (r2 - 11) = 0
⇒ (r2 - 11) (r2 - 3) = 0
⇒ r2 = 11 or r2 = 3
⇒ r1 = 14 - 11 = 3 or r1 = 14 - 3 = 11
Thus, the radii of two circles are 11 cm and 3 cm respectively.
Solution 27

Solution 28

Solution 29