Class 10 SELINA Solutions Maths Chapter 15 - Similarity (With Applications to Maps and Models)
Similarity (With Applications to Maps and Models) Exercise Ex. 15(A)
Solution 2(i)

Solution 2(ii)

Solution 3(i)
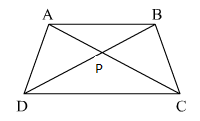

Solution 3(ii)


Solution 4(i)
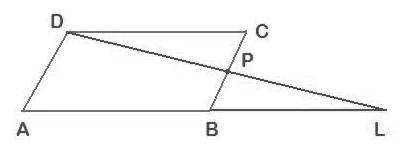

Solution 4(ii)


Solution 5(i)
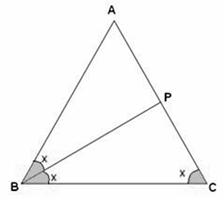

Solution 5(ii)




Solution 6
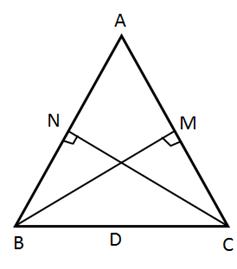

Solution 7(i)

Solution 7(ii)
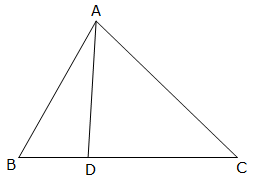
In ΔADE and ΔABC
Solution 8

Solution 9

Solution 10
(i) False
(ii) True
(iii) True
(iv) False
(v) True
(vi) True
(vii) True
Solution 11

Solution 12
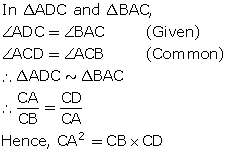
Solution 13
(i) In ∆ ABC and ∆ AMP,
![]() BAC=
BAC= ![]() PAM [Common]
PAM [Common]
![]() ABC=
ABC= ![]() PMA [Each = 90°]
PMA [Each = 90°]
∆ ABC ~ ∆ AMP [AA Similarity]
(ii)
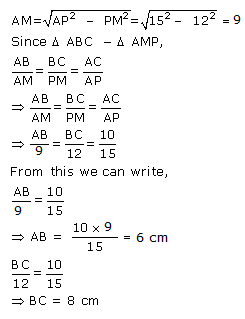
Solution 14
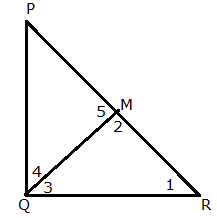
(i) In ![]() PQM and
PQM and ![]() PQR,
PQR,
![]() PMQ =
PMQ = ![]() PQR = 90o
PQR = 90o
![]() QPM =
QPM = ![]() RPQ (Common)
RPQ (Common)
![]()
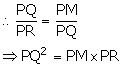
(ii) In ![]() QMR and
QMR and ![]() PQR,
PQR,
![]() QMR =
QMR = ![]() PQR = 90o
PQR = 90o
![]() QRM =
QRM = ![]() QRP (Common)
QRP (Common)
![]()
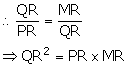
(iii) Adding the relations obtained in (i) and (ii), we get,
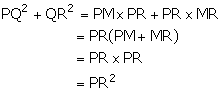
Solution 15

(i) In ![]() CDB,
CDB,
![]() 1 +
1 + ![]() 2 +
2 +![]() 3 = 180o
3 = 180o
![]() 1 +
1 + ![]() 3 = 90o ..... (1)(Since,
3 = 90o ..... (1)(Since, ![]() 2 = 90o)
2 = 90o)
![]() 3 +
3 + ![]() 4 = 90o .....(2) (Since,
4 = 90o .....(2) (Since, ![]() ABC = 90o)
ABC = 90o)
From (1) and (2),
![]() 1 +
1 + ![]() 3 =
3 = ![]() 3 +
3 + ![]() 4
4
![]() 1 =
1 = ![]() 4
4
Also, ![]() 2 =
2 = ![]() 5 = 90o
5 = 90o

Hence, AD = 6.4 cm

(iii)
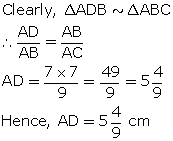
Solution 16

Solution 17
Given, AD2 = BD ![]() DC
DC
![]()
![]()
So, these two triangles will be equiangular.

Solution 18
(i) The three pair of similar triangles are:
![]() BEF and
BEF and ![]() BDC
BDC
![]() CEF and
CEF and ![]() CAB
CAB
![]() ABE and
ABE and ![]() CDE
CDE
(ii) Since, ![]() ABE and
ABE and ![]() CDE are similar,
CDE are similar,

Since, ![]() CEF and
CEF and ![]() CAB are similar,
CAB are similar,

Solution 19
(i) Given, AP: PB = 4: 3.
Since, PQ || AC. Using Basic Proportionality theorem,

Now, ![]() PQB =
PQB = ![]() ACB (Corresponding angles)
ACB (Corresponding angles)
![]() QPB =
QPB = ![]() CAB (Corresponding angles)
CAB (Corresponding angles)
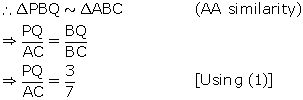
(ii) ![]() ARC =
ARC = ![]() QSP = 90o
QSP = 90o
![]() ACR =
ACR = ![]() SPQ (Alternate angles)
SPQ (Alternate angles)

Solution 20
We have:

Solution 21
(i) Since, BD and CE are medians.
AD = DC
AE = BE
Hence, by converse of Basic Proportionality theorem,
ED || BC
In ![]() EGD and
EGD and ![]() CGB,
CGB,

(ii) Since, ![]()
![]()
In ![]() AED and
AED and ![]() ABC,
ABC,

From (1),

Similarity (With Applications to Maps and Models) Exercise Ex. 15(B)
Solution 2(i)
![]()
Now, DE is parallel to BC.
Then, by Basic proportionality theorem, we have

Solution 2(ii)
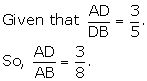
Solution 2(iii)

Solution 2(iv)

Solution 2(v)

Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 4
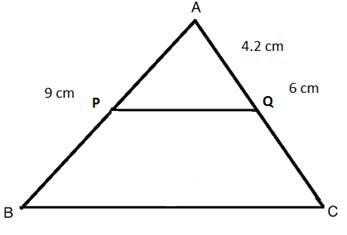

Solution 5(i)
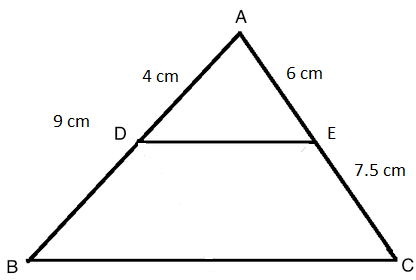

Solution 5(ii)
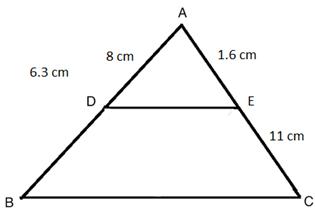

Solution 6
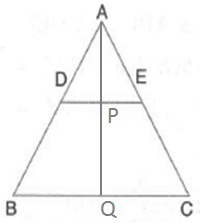


Solution 7
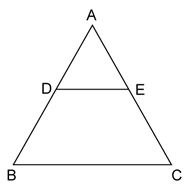
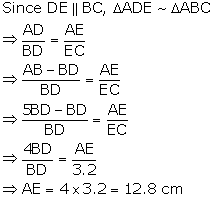
Solution 8
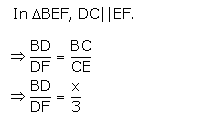

Similarly

Solution 9

Solution 10

Solution 11

Similarity (With Applications to Maps and Models) Exercise Ex. 15(C)
Solution 2
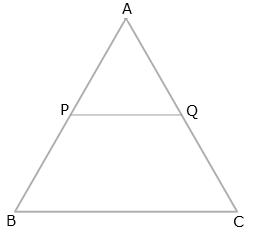
(i) AP =![]() PB
PB ![]()

(ii)

Solution 3
Let ![]()

Solution 4
Given, ![]()
(i)

(ii)
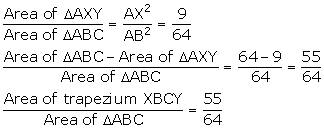
Solution 5

From the given information, we have:
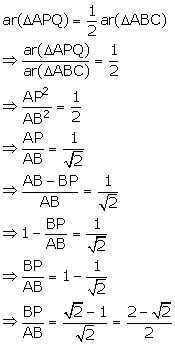
Solution 6
(i)

(ii) Since ![]() LMN and
LMN and ![]() MNR have common vertex at M and their bases LN and NR are along the same straight line
MNR have common vertex at M and their bases LN and NR are along the same straight line

(iii) Since ![]() LQM and
LQM and ![]() LQN have common vertex at L and their bases QM and QN are along the same straight line
LQN have common vertex at L and their bases QM and QN are along the same straight line
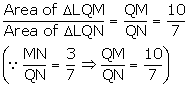
Solution 7


Solution 8

Solution 9

(i) Given, DE || BC and ![]()
In ![]() ADE and
ADE and ![]() ABC,
ABC,
![]() A =
A = ![]() A(Corresponding Angles)
A(Corresponding Angles)
![]() ADE =
ADE = ![]() ABC(Corresponding Angles)
ABC(Corresponding Angles)
![]()
![]() (By AA- similarity)
(By AA- similarity)
![]()
![]() ..........(1)
..........(1)
Now![]()
Using (1), we get![]() .........(2)
.........(2)
(ii) In ![]() DEF and
DEF and ![]() CBF,
CBF,
![]() FDE =
FDE = ![]() FCB(Alternate Angle)
FCB(Alternate Angle)
![]() DFE =
DFE = ![]() BFC(Vertically Opposite Angle)
BFC(Vertically Opposite Angle)
![]()
![]() DEF
DEF ![]()
![]() CBF(By AA- similarity)
CBF(By AA- similarity)
![]() using (2)
using (2)
![]() .
.
(iii) Since the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides, therefore
![]()
Solution 10
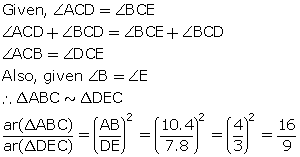
Similarity (With Applications to Maps and Models) Exercise Ex. 15(D)
Solution 2(i)

Solution 2(ii)

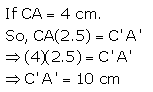
Solution 3(i)

Solution 3(ii)

Solution 4(i)
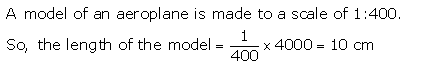
Solution 4(ii)
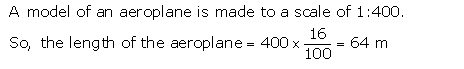
Solution 5
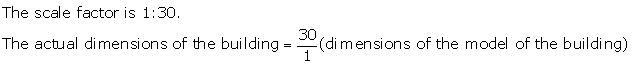

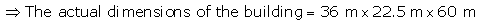
Solution 6(i)

Solution 6(ii)

Solution 7
![]()
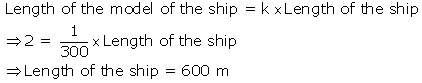

Similarity (With Applications to Maps and Models) Exercise TEST YOURSELF
Solution 2(i)
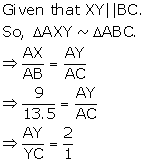
Solution 2(ii)
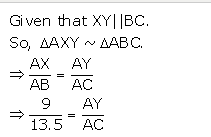

Solution 2(iii)
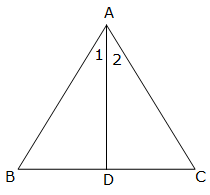
Given that XY || BC
So, △AXY ∼ △ABC
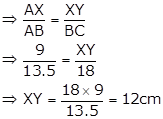
Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 4

Solution 5
Triangle ABC is similar to triangle PQR

Solution 6

Solution 7

Solution 8
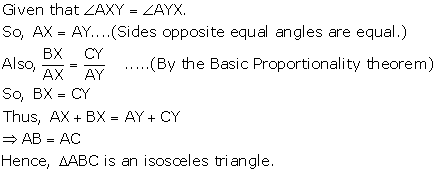
Solution 9

Solution 10(i)

Solution 10(ii)

Solution 11(i)

Solution 11(ii)

Solution 11(iii)

Solution 12

BF + FE = 2BF
Hence,
FE = BF
(ii) In ![]() AFD, EG || FD. Using Basic Proportionality theorem,
AFD, EG || FD. Using Basic Proportionality theorem,
![]() … (1)
… (1)
Now, AE = EB (as E is the mid-point of AB)
AE = 2EF (Since, EF = FB, by (i))
From (1),
![]()
Hence, AG: GD = 2: 1.
Solution 13
Let us assume two similar triangles as ![]() ABC
ABC ![]()
![]() PQR
PQR

Solution 14
The ratio between the altitudes of two similar triangles is same as the ratio between their sides.
(i) The ratio between the medians of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 3: 5
Required ratio = 3: 5
(ii) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 3: 5
Required ratio = 3: 5
(iii) The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.
![]() Required ratio = (3)2 : (5)2 = 9: 25
Required ratio = (3)2 : (5)2 = 9: 25
Solution 15
The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.
So, the ratio between the sides of the two triangles = 4: 5
(i) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
(ii) The ratio between the altitudes of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
(iii) The ratio between the medians of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
Solution 16
Scale :- 1 : 20000
1 cm represents 20000 cm= ![]() = 0.2 km
= 0.2 km
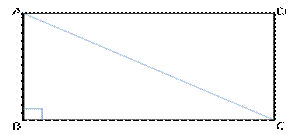
(i)
![]()
= ![]()
= 576 + 1024 = 1600
AC = 40 cm
Actual length of diagonal = 40 ![]() 0.2 km = 8 km
0.2 km = 8 km
(ii)
1 cm represents 0.2 km
1 cm2 represents 0.2 ![]() 0.2
0.2 ![]()
The area of the rectangle ABCD = AB ![]() BC
BC
= 24 ![]() 32 = 768
32 = 768![]()
Actual area of the plot = 0.2 ![]() 0.2
0.2 ![]() 768
768 ![]() = 30.72 km2
= 30.72 km2
Solution 17
The dimensions of the building are calculated as below.
Length = 1 ![]() 50 m = 50 m
50 m = 50 m
Breadth = 0.60 ![]() 50 m = 30 m
50 m = 30 m
Height = 1.20 ![]() 50 m = 60 m
50 m = 60 m
Thus, the actual dimensions of the building are 50 m ![]() 30 m
30 m ![]() 60 m.
60 m.
(i)
Floor area of the room of the building ![]()
(ii)
Volume of the model of the building
![]()
![]()
Solution 18

(iii)

Solution 19
Triangle ABC is enlarged to DEF. So, the two triangles will be similar.
![]()
Longest side in ![]() ABC = BC = 6 cm
ABC = BC = 6 cm
Corresponding longest side in ![]() DEF = EF = 9 cm
DEF = EF = 9 cm
Scale factor = ![]() = 1.5
= 1.5
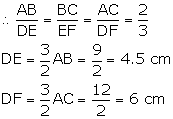
Solution 20
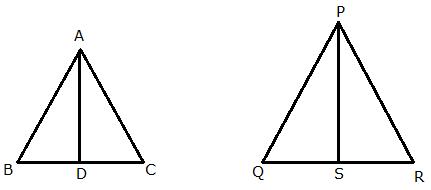
Let ABC and PQR be two isosceles triangles.
Then, ![]()
Also, ![]() A =
A = ![]() P (Given)
P (Given)
![]()
Let AD and PS be the altitude in the respective triangles.
We know that the ratio of areas of two similar triangles is equal to the square of their corresponding altitudes.

Solution 21
In triangle ABC, PO || BC. Using Basic proportionality theorem,
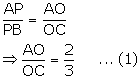
(i)
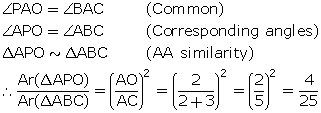
(ii)
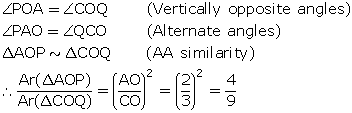
Solution 22
In ![]() ABC and
ABC and ![]() EBD,
EBD,
![]() ACB =
ACB = ![]() EDB (given)
EDB (given)
![]() ABC =
ABC = ![]() EBD (common)
EBD (common)
![]() (by AA- similarity)
(by AA- similarity)
(i) We have, ![]()
(ii) ![]()

Solution 23

Solution 24(i)

Solution 24(ii)

Solution 24(iii)

Solution 25
(i) In ![]() AGB, DE || AB , by Basic proportionality theorem,
AGB, DE || AB , by Basic proportionality theorem,
![]() .... (1)
.... (1)
In ![]() GBC, EF || BC, by Basic proportionality theorem,
GBC, EF || BC, by Basic proportionality theorem,
![]() .... (2)
.... (2)
From (1) and (2), we get,
![]()
![]()
(ii)
From (i), we have:

Solution 26
i.
In ∆PQR and ∆SPR,
∠PSR = ∠QPR … given
∠PRQ = ∠PRS … common angle
⇒ ∆PQR ∼ ∆SPR (AA Test)
ii. Find the lengths of QR and PS.
Since ∆PQR ∼ ∆SPR … from (i)
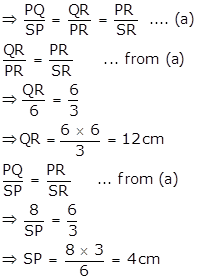
iii.
![]()

