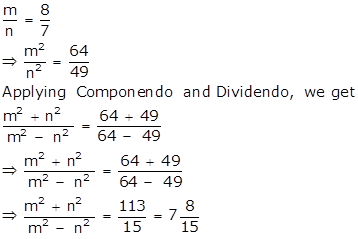Class 10 SELINA Solutions Maths Chapter 7 - Ratio and Proportion (Including Properties and Uses)
Ratio and Proportion (Including Properties and Uses) Exercise Ex. 7(A)
Solution 1(a)
Correct Option: (ii) 49 : 25
A : B = 7 : 5 ![]()
B : C = 7 : 5 ![]()
Then, ![]()
Solution 1(b)
Correct Option: (iv) ![]()
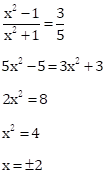
Solution 1(c)
Correct Option: (iii) 1 : 6
(2x + 3y) : (3x + 2y) = 4 : 3
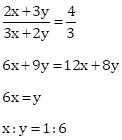
Solution 1(d)
Correct Option: (ii) 50 and 80
Since the ratio between the numbers is 5 : 8, if one number is 5x, the other number is 8x.
Now,
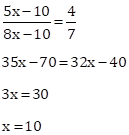
Then, 5x = 5(10) = 50 and 8x = 8(10) = 80
Solution 1(e)
Correct Option: (iii) 1 : 1
Compound ratio of x – y : x + y and (x + y)2 : x2 – y2
= (x – y)(x + y)2 : (x + y)(x2 – y2)
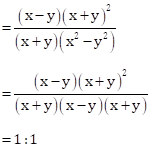
Solution 1(f)
Correct Option: (i) x : 2y
Sub-duplicate ratio of 6x2 : 24y2
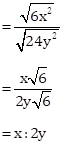
Solution 2
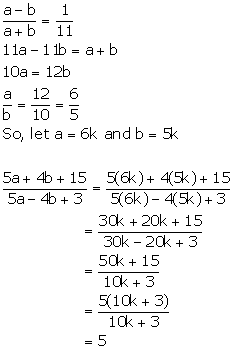
Hence, (5a + 4b + 15): (5a - 4b + 3) = 5: 1
Solution 3

Solution 4

Solution 5
x2 + 6y2 = 5xy
Dividing both sides by y2, we get,

Solution 6
Given,
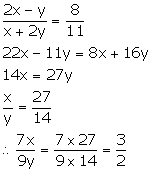
Solution 7
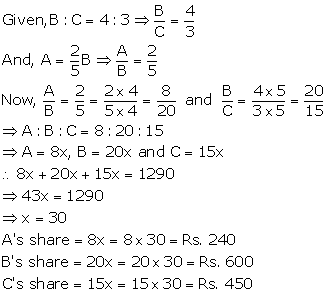
Solution 8
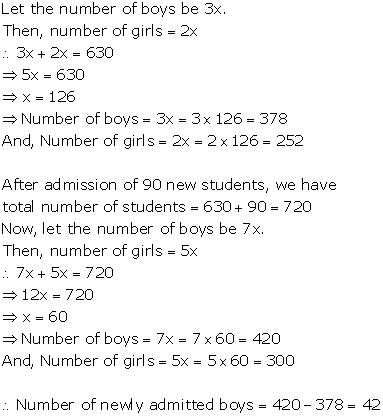
Solution 9
Let x be subtracted from each term of the ratio 9: 17.
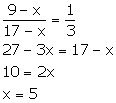
Thus, the required number which should be subtracted is 5.
Solution 10

Solution 11
Assuming that all the men do the same amount of work in one day and one day work of each man = 1 units, we have,
Amount of work done by (x - 2) men in (4x + 1) days
= Amount of work done by (x - 2)(4x + 1) men in one day
= (x - 2)(4x + 1) units of work
Similarly,
Amount of work done by (4x + 1) men in (2x - 3) days
= (4x + 1)(2x - 3) units of work
According to the given information,
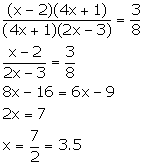
Solution 12
According to the given information,
Increased (new) bus fare = ![]() original bus fare
original bus fare
(i) We have:
Increased (new) bus fare = ![]() Rs 245 = Rs 315
Rs 245 = Rs 315
![]() Increase in fare = Rs 315 - Rs 245 = Rs 70
Increase in fare = Rs 315 - Rs 245 = Rs 70
(ii) We have:
Rs 207 = ![]() original bus fare
original bus fare
Original bus fare = ![]()
![]() Increase in fare = Rs 207 - Rs 161 = Rs 46
Increase in fare = Rs 207 - Rs 161 = Rs 46
Solution 13
Let the cost of the entry ticket initially and at present be 10 x and 13x respectively.
Let the number of visitors initially and at present be 6y and 5y respectively.
Initially, total collection = 10x ![]() 6y = 60 xy
6y = 60 xy
At present, total collection = 13x ![]() 5y = 65 xy
5y = 65 xy
Ratio of total collection = 60 xy: 65 xy = 12: 13
Thus, the total collection has increased in the ratio 12: 13.
Solution 14
Let the original number of oranges and apples be 7x and 13x.
According to the given information,
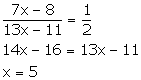
Thus, the original number of oranges and apples are 7 ![]() 5 = 35 and 13
5 = 35 and 13 ![]() 5 = 65 respectively.
5 = 65 respectively.
Solution 15

Solution 16(i)
3A = 4B = 6C
3A = 4B ![]()
4B = 6C ![]()
Hence, A: B: C = 4: 3: 2
Solution 16(ii)
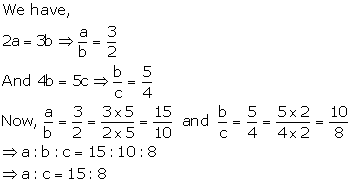
Solution 17
(i) Required compound ratio = 2 ![]() 9
9 ![]() 14: 3
14: 3 ![]() 14
14 ![]() 27
27
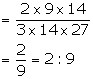
(ii) Required compound ratio = 2a ![]() mn
mn![]() x: 3b
x: 3b ![]() x2
x2![]() n
n
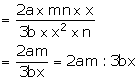
(iii) Required compound ratio = ![]()

Solution 18

Solution 19
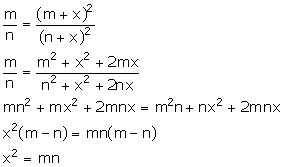
Solution 20

Solution 21
Reciprocal ratio of 15: 28 = 28: 15
Sub-duplicate ratio of 36: 49 = ![]()
Triplicate ratio of 5: 4 = 53: 43 = 125: 64
Required compounded ratio
= ![]()
Ratio and Proportion (Including Properties and Uses) Exercise Ex. 7(B)
Solution 1(a)
Correct Option: (iii) 0.4 and 50
x, 2, 10 and y are in continued proportion.
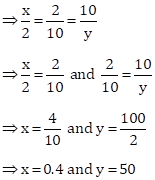
Solution 1(b)
Correct Option: (i) 9 : 4
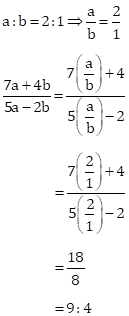
Solution 1(c)
Correct Option: (iii) x : z
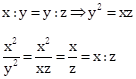
Solution 1(d)
Correct Option: (i) 1
Let b be the mean proportional between ![]() .
.
Then,
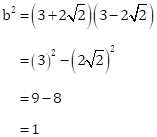
Therefore, b = 1
Solution 1(e)
Correct Option: (i) ![]()
2x, 9 and 18 are in continued proportion.
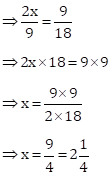
Solution 2
(i) Let the fourth proportional to 1.5, 4.5 and 3.5 be x.
![]() 1.5 : 4.5 = 3.5 : x
1.5 : 4.5 = 3.5 : x
![]() 1.5
1.5 ![]() x = 3.5
x = 3.5 ![]() 4.5
4.5
![]() x = 10.5
x = 10.5
(ii) Let the fourth proportional to 3a, 6a2 and 2ab2 be x.
![]() 3a : 6a2 = 2ab2 : x
3a : 6a2 = 2ab2 : x
![]() 3a
3a ![]() x = 2ab2
x = 2ab2![]() 6a2
6a2
![]() 3a
3a ![]() x = 12a3b2
x = 12a3b2
![]() x = 4a2b2
x = 4a2b2
Solution 3
(i) Let the third proportional to 2![]() and 4 be x.
and 4 be x.
![]() 2
2![]() , 4, x are in continued proportion.
, 4, x are in continued proportion.
![]() 2
2![]() : 4 = 4 : x
: 4 = 4 : x
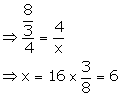
(ii) Let the third proportional to a - b and a2 - b2 be x.
![]() a - b, a2 - b2, x are in continued proportion.
a - b, a2 - b2, x are in continued proportion.
![]() a - b : a2 - b2 = a2 - b2 : x
a - b : a2 - b2 = a2 - b2 : x
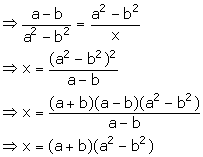
Solution 4
(i) Let the mean proportional between 6 + 3![]() and 8 - 4
and 8 - 4![]() be x.
be x.
![]() 6 + 3
6 + 3![]() , x and 8 - 4
, x and 8 - 4![]() are in continued proportion.
are in continued proportion.
![]() 6 + 3
6 + 3![]() : x = x : 8 - 4
: x = x : 8 - 4![]()
![]() x
x ![]() x = (6 + 3
x = (6 + 3![]() ) (8 - 4
) (8 - 4![]() )
)
![]() x2 = 48 + 24
x2 = 48 + 24![]() - 24
- 24![]() - 36
- 36
![]() x2 = 12
x2 = 12
![]() x= 2
x= 2![]()
(ii) Let the mean proportional between a - b and a3 - a2b be x.
![]() a - b, x, a3 - a2b are in continued proportion.
a - b, x, a3 - a2b are in continued proportion.
![]() a - b : x = x : a3 - a2b
a - b : x = x : a3 - a2b
![]() x
x ![]() x = (a - b) (a3 - a2b)
x = (a - b) (a3 - a2b)
![]() x2 = (a - b) a2(a - b) = [a(a - b)]2
x2 = (a - b) a2(a - b) = [a(a - b)]2
![]() x = a(a - b)
x = a(a - b)
Solution 5
Given, x + 5 is the mean proportion between x + 2 and x + 9.
![]() (x + 2), (x + 5) and (x + 9) are in continued proportion.
(x + 2), (x + 5) and (x + 9) are in continued proportion.
![]() (x + 2) : (x + 5) = (x + 5) : (x + 9)
(x + 2) : (x + 5) = (x + 5) : (x + 9)
![]() (x + 5)2 = (x + 2)(x + 9)
(x + 5)2 = (x + 2)(x + 9)
![]() x2 + 25 + 10x = x2 + 2x + 9x + 18
x2 + 25 + 10x = x2 + 2x + 9x + 18
![]() 25 - 18 = 11x - 10x
25 - 18 = 11x - 10x
![]() x = 7
x = 7
Solution 6
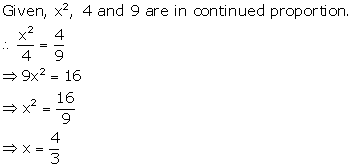
Solution 7
Since y is the mean proportion between x and z
Therefore, y2 = xz
Now, we have to prove that xy+yz is the mean proportional between x2+y2 and y2+z2, i.e.,

LHS = RHS
Hence, proved.
Solution 8
Given, q is the mean proportional between p and r.
![]() q2 = pr
q2 = pr
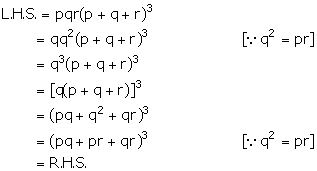
Solution 9
Let x, y and z be the three quantities which are in continued proportion.
Then, x : y :: y : z ![]() y2 = xz ....(1)
y2 = xz ....(1)
Now, we have to prove that
x : z = x2 : y2
That is we need to prove that
xy2 = x2z
LHS = xy2 = x(xz) = x2z = RHS [Using (1)]
Hence, proved.
Solution 10
Let the required third proportional be p.
![]()
![]() , p are in continued proportion.
, p are in continued proportion.

Solution 11
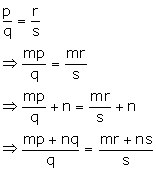
Hence, mp + nq : q = mr + ns : s.
Solution 12

Hence, proved.
Ratio and Proportion (Including Properties and Uses) Exercise Ex. 7(C)
Solution 1(a)
Correct Option: (iv) –1
x + y + z = 0 ⇒ x = –(y + z)
![]()
Solution 1(b)
Correct Option: (ii) a2 : c2
a, b, c and d are in proportion.
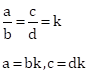
Now,
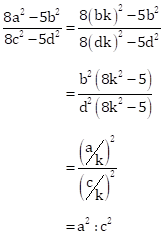
Solution 1(c)
Correct Option: (iii) 2
![]()
x + y = kz
y + z = kx
z + x = ky
(x + y) + (y + z) + (z + x) = kz + kx + ky
2(x + y + z) = k(x + y + z)
k = 2
Solution 1(d)
Correct Option: (ii) ±4
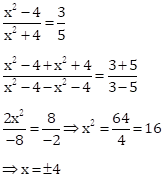
Solution 1(e)
Correct Option: (i) 35
![]()
x = 5(a + b – c)
y = 5(b + c – a)
z = 5(c + a – b)
x + y + z = 5[a + b – c + b + c – a + c + a – b]
= 5(a + b + c)
= 5(7)
= 35
Solution 2

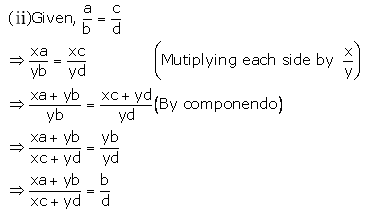
Solution 3
Given, ![]()
Applying componendo and dividendo,
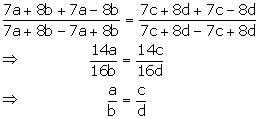
Hence, a: b = c: d.
Solution 4
(i) x = ![]()

(ii) ![]()
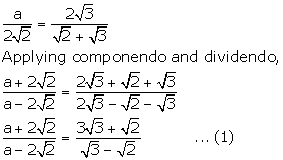

Solution 5

Solution 6

Solution 7
Given, ![]()
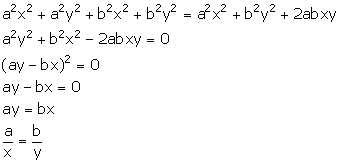
Solution 8
Given, a, b and c are in continued proportion.

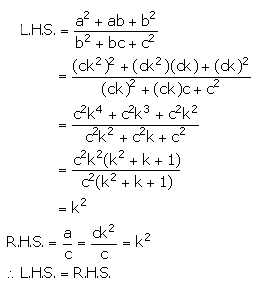
Solution 9


Solution 10
Since, ![]()
Applying componendo and dividendo, we get,
![]()
![]()
Squaring both sides,
![]()
Again applying componendo and dividendo,
![]()
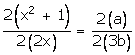
![]()
3bx2 + 3b = 2ax
3bx2 - 2ax + 3b = 0.
Solution 11

Solution 12
![]()
Applying componendo and dividendo,
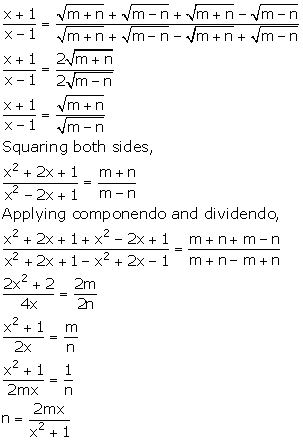
Solution 13
![]()
Applying componendo and dividendo,

Ratio and Proportion (Including Properties and Uses) Exercise TEST YOURSELF
Solution 1(a)
Correct Option: (iii) 1
Let b be the mean proportional of ![]() .
.
Then,

Therefore, b = 1
Solution 1(b)
Correct Option: (iv) ![]()
(a + b) : (a – b) = 13 : 3

Solution 1(c)
Correct Option: (iii) A = 9, B = 32
x is directly proportional to y.
Then,
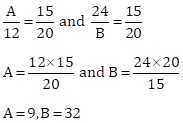
Solution 1(d)
Correct Option: (i) 3 : 7
(m + n) : (n – m) = 5 : 2
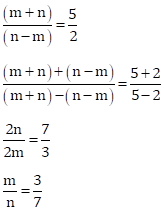
Solution 1(e)
Correct Option: (ii) 2 : 1
x = y ![]()
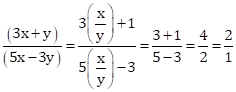
Solution 2
Given, ![]()
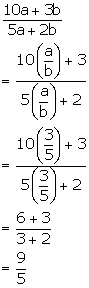
Solution 3
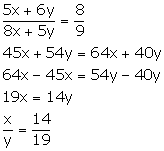
Solution 4
(i) Duplicate ratio of ![]()
(ii) Triplicate ratio of 2a: 3b = (2a)3: (3b)3 = 8a3 : 27b3
(iii) Sub-duplicate ratio of 9x2a4 : 25y6b2 = ![]()
(iv) Sub-triplicate ratio of 216: 343 = ![]()
(v) Reciprocal ratio of 3: 5 = 5: 3
(vi) Duplicate ratio of 5: 6 = 25: 36
Reciprocal ratio of 25: 42 = 42: 25
Sub-duplicate ratio of 36: 49 = 6: 7
Required compound ratio = ![]()
Solution 5
(i) (2x + 3): (5x - 38) is the duplicate ratio of ![]()
Duplicate ratio of ![]()
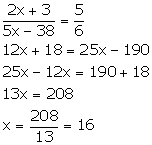
(ii) (2x + 1): (3x + 13) is the sub-duplicate ratio of 9: 25
Sub-duplicate ratio of 9: 25 = 3: 5

(iii) (3x - 7): (4x + 3) is the sub-triplicate ratio of 8: 27
Sub-triplicate ratio of 8: 27 = 2: 3
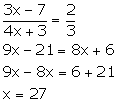
Solution 6
Let the required quantity which is to be added be p.
Then, we have:
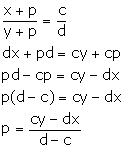
Solution 7

Solution 8
15(2x2 - y2) = 7xy

Solution 9
(i) Let the fourth proportional to 2xy, x2 and y2 be n.
![]() 2xy: x2 = y2: n
2xy: x2 = y2: n
![]() 2xy
2xy ![]() n = x2
n = x2![]() y2
y2
![]() n =
n =![]()
(ii) Let the third proportional to a2 - b2 and a + b be n.
![]() a2 - b2, a + b and n are in continued proportion.
a2 - b2, a + b and n are in continued proportion.
![]() a2 - b2 : a + b = a + b : n
a2 - b2 : a + b = a + b : n
![]() n =
n =![]()
(iii) Let the mean proportion to (x - y) and (x3 - x2y) be n.
![]() (x - y), n, (x3 - x2y) are in continued proportion
(x - y), n, (x3 - x2y) are in continued proportion
![]() (x - y) : n = n : (x3 - x2y)
(x - y) : n = n : (x3 - x2y)
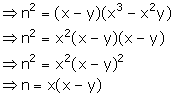
Solution 10
Let the required numbers be a and b.
Given, 14 is the mean proportional between a and b.
![]() a: 14 = 14: b
a: 14 = 14: b
![]() ab = 196
ab = 196
![]()
Also, given, third proportional to a and b is 112.
![]() a: b = b: 112
a: b = b: 112
![]()
Using (1), we have:
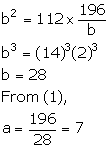
Thus, the two numbers are 7 and 28.
Solution 11
Given, ![]()
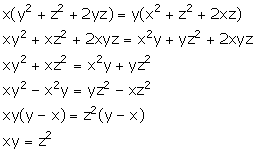
Hence, z is mean proportional between x and y.
Solution 12
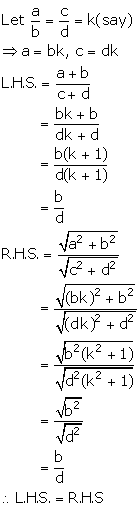
Solution 13
Ratio of number of boys to the number of girls = 3: 1
Let the number of boys be 3x and number of girls be x.
![]() 3x + x = 36
3x + x = 36
4x = 36
x = 9
![]() Number of boys = 27
Number of boys = 27
Number of girls = 9
Le n number of girls be added to the council.
From given information, we have:
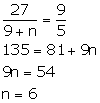
Thus, 6 girls are added to the council.
Solution 14
7x - 15y = 4x + y
7x - 4x = y + 15y
3x = 16y
![]()

Solution 15
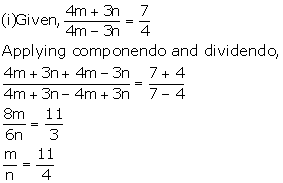

Solution 16
![]() x, y, z are in continued proportion,
x, y, z are in continued proportion,
![]()
![]()
Therefore,
![]()
![]()
![]() (By alternendo)
(By alternendo)
![]()
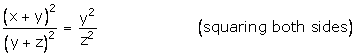
![]()

![]()

Hence Proved.
Solution 17
x = 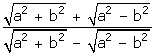
By componendo and dividendo,

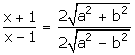
Squaring both sides,
![]()
By componendo and dividendo,
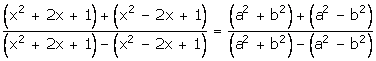
![]()
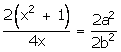
![]()
![]()
![]() b2 =
b2 = ![]()
Hence Proved.
Solution 18

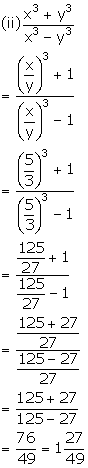
Solution 19

Solution 20
![]()

Solution 21
Given that b is the mean proportion between a and c.
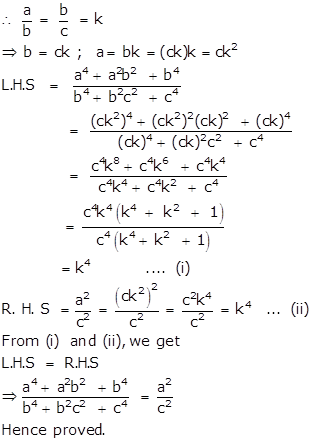
Solution 22
i.
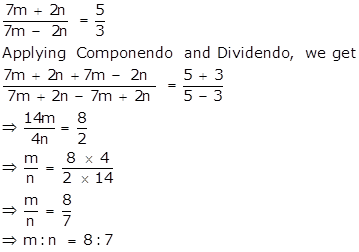
ii.
From (i),