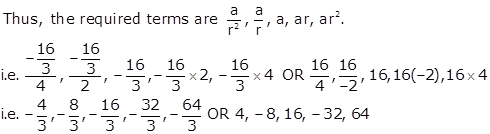Class 10 SELINA Solutions Maths Chapter 11 - Geometric Progression
Ex. 11(A)
Ex. 11(B)
Geometric Progression Exercise Ex. 11(A)
Solution 8
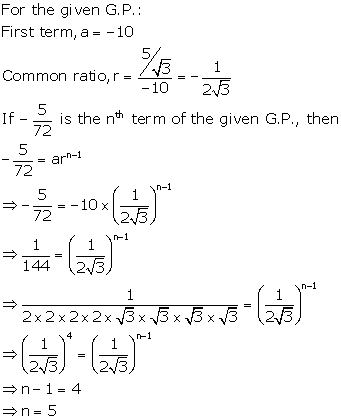
Solution 18

Solution 9

Solution 19

Solution 10
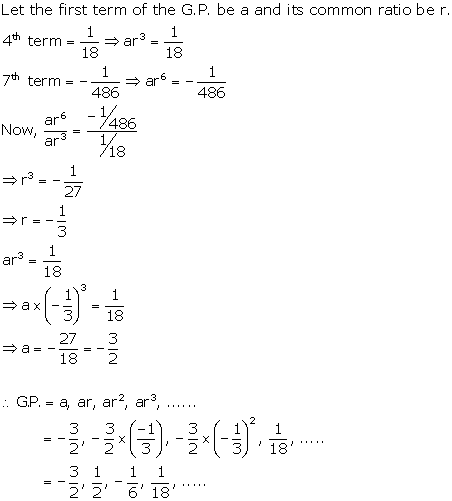
Solution 20
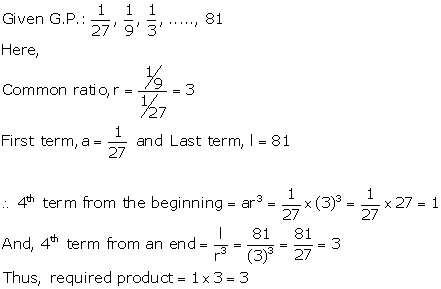
Solution 11

Solution 2

Solution 12

Solution 3

Solution 13

Solution 4

Solution 14

Solution 15

Solution 21(i)
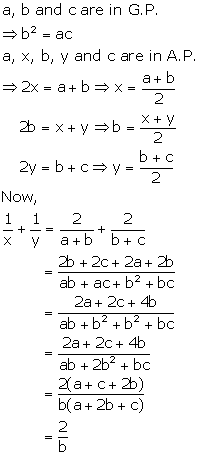
Solution 5

Solution 16

Solution 21(ii)
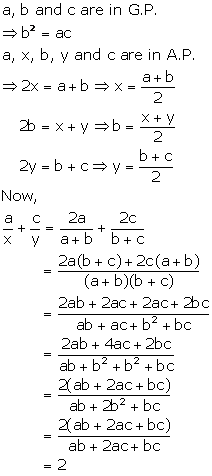
Solution 17

Solution 22
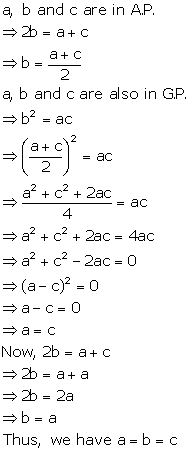
Solution 6

Solution 7
Given series: 2, - 6, 18, - 54 ……
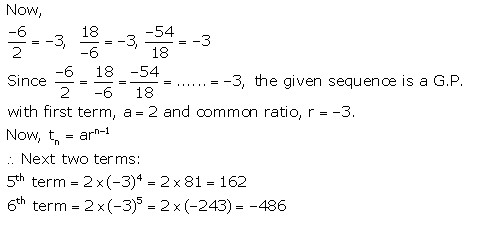
Geometric Progression Exercise Ex. 11(B)
Solution 2(i)

Solution 2(ii)

Solution 2(iii)
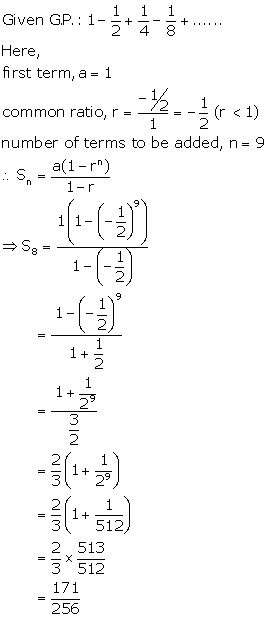
Solution 2(iv)

Solution 2(v)

Solution 2(vi)

Solution 3

Solution 4

Solution 5
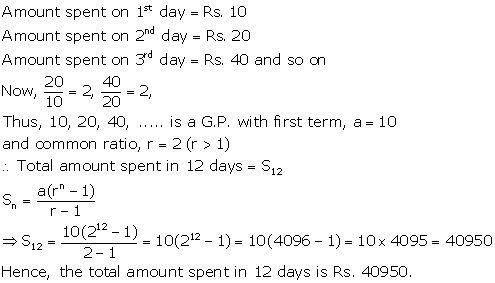
Solution 6

Solution 7
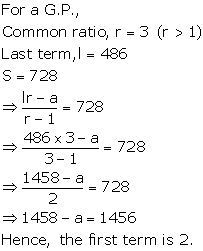
Solution 8

Solution 9

Solution 10
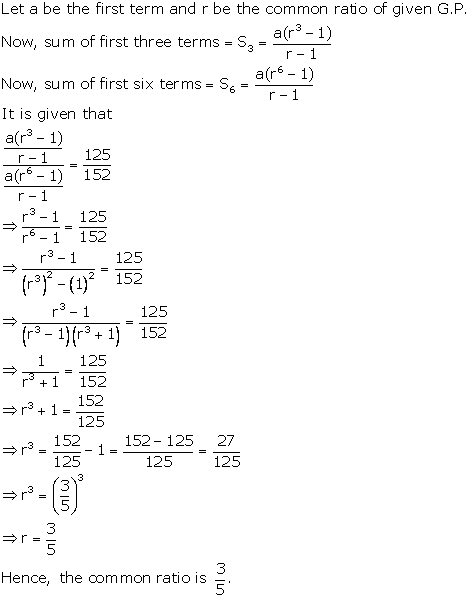
Solution 11
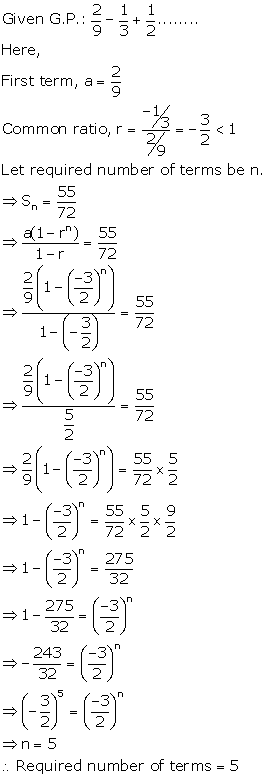
Solution 12
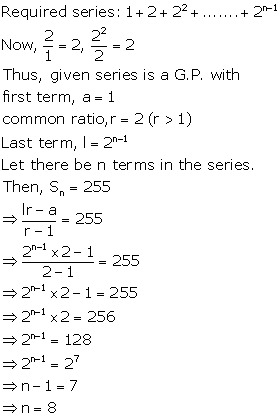
Solution 13(i)
![]()
Solution 13(ii)
![]()
Solution 13(iii)
![]()
Solution 14
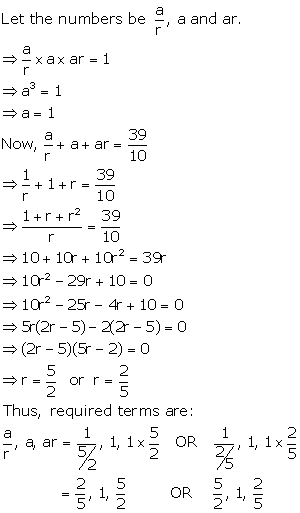
Solution 15

Solution 16
First term (a) = ![]()
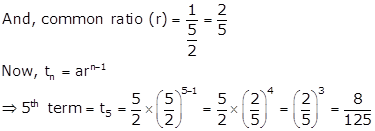
Solution 17
First term (a) = 125
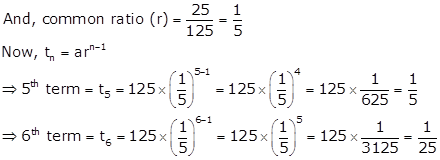
Solution 18
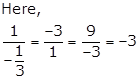
Thus, the given sequence is a G.P. with ![]()
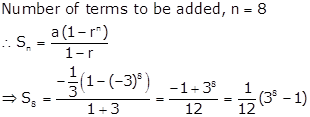
Solution 19
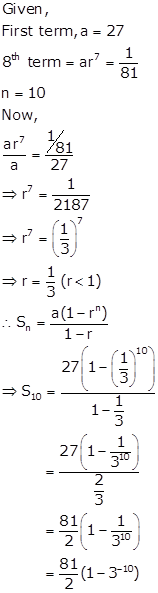
Solution 20
Let the five terms of the given G.P. be
![]()
Given, sum of first two terms = -4
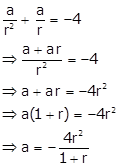
And, 5th term = 4(3rd term)
⇒ ar2 = 4(a)
⇒ r2 = 4
⇒ r = ±2
When r = +2,
![]()
When r = -2,
![]()