Class 10 SELINA Solutions Maths Chapter 17 - Circles
Circles Exercise Ex. 17(A)
Solution 2
Solution 3
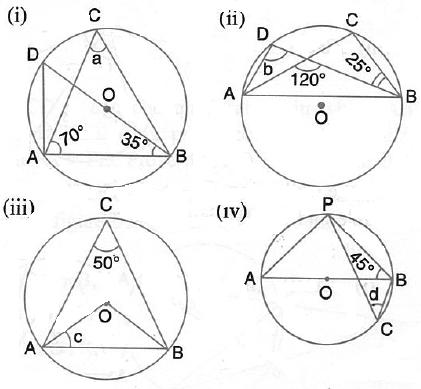
Solution 4
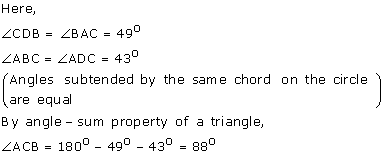
Solution 5
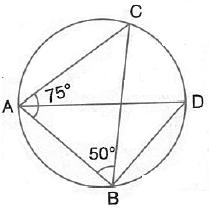
Solution 6
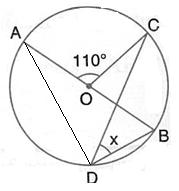
Solution 7
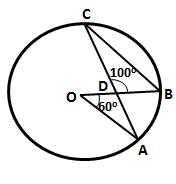
Solution 8
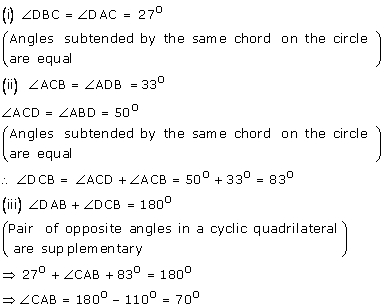
Solution 9
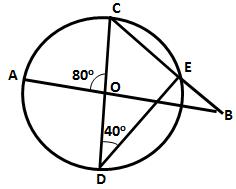
Solution 10
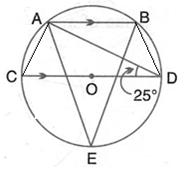
Solution 11
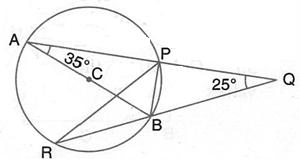
Solution 12
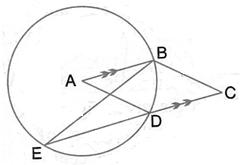
Solution 13
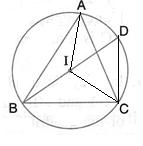
Solution 14
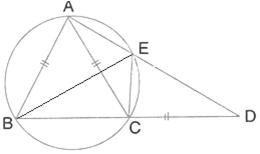
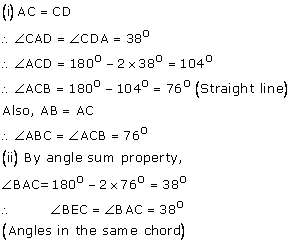
Solution 15
Solution 16
Solution 17
Solution 18
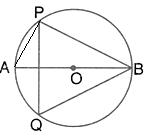
Solution 19
Circles Exercise Ex. 17(B)
Solution 2
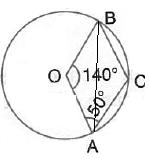
Solution 3
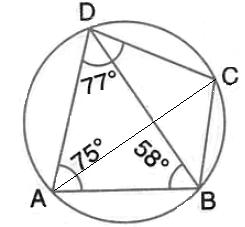
Solution 4
Solution 5
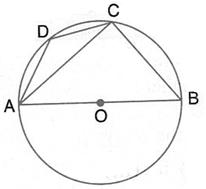
Solution 6
Solution 7
Solution 8
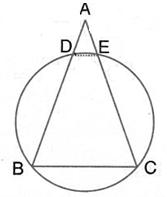
Solution 9
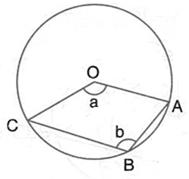
Solution 10
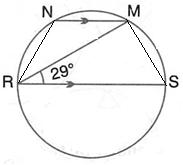
Solution 11
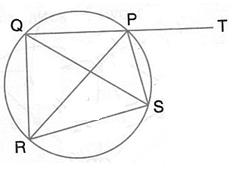
Solution 12
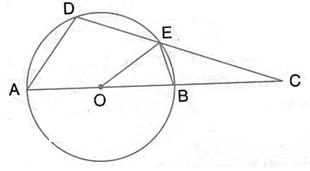
Solution 13
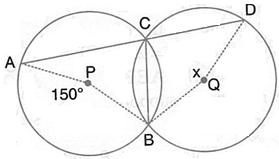
Solution 14
Solution 15
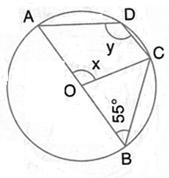
Solution 16
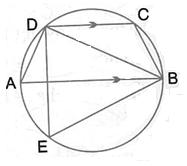
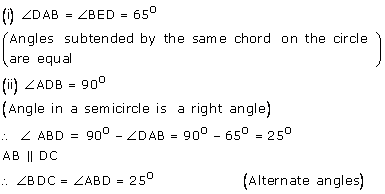
Solution 17
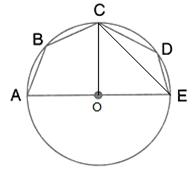
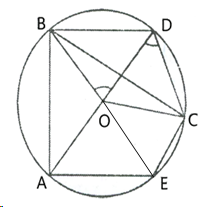
(i) 
AEB = 
(Angle in a semicircle is a right angle)
Therefore EBA = - EAB = - 
= 
(ii) AB 
ED
Therefore DEB = EBA = (Alternate angles)
Therefore BCDE is a cyclic quadrilateral
Therefore DEB + BCD = 
[Pair of opposite angles in a cyclic quadrilateral are supplementary]
Therefore BCD = - = 
Solution 18
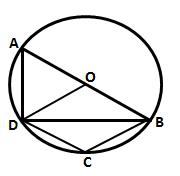
Solution 19
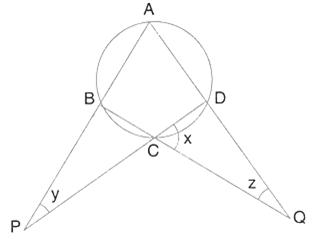
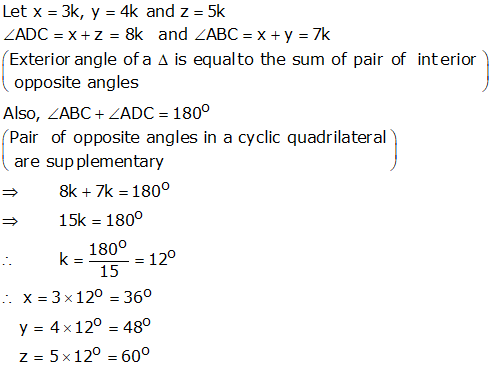
Solution 20
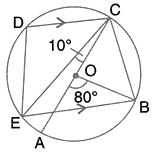
Solution 21
Solution 22
Solution 23
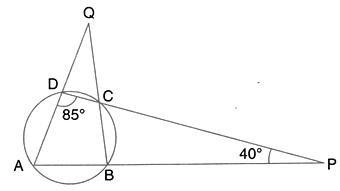
Solution 24
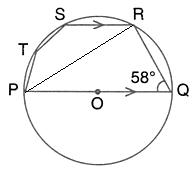
Solution 25
Solution 26
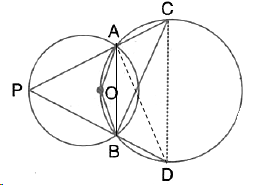
Solution 27
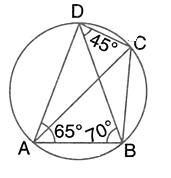
Solution 28
Circles Exercise Ex. 17(C)
Solution 2
Solution 3
Solution 4
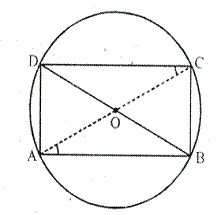
Solution 5
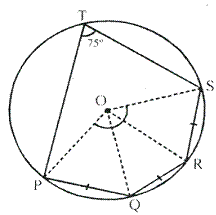
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Circles Exercise TEST YOURSELF
Solution 2
Solution 3
Solution 4
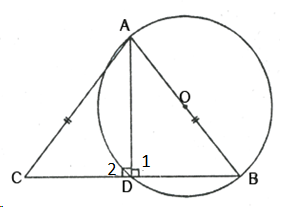
Given - In Δ ABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC at D.
To prove - D is the midpoint of BC.
Construction - Join AD.
Proof:
∠1 = 90° [Angle in a semi circle]
But ∠1 + ∠2 = 180° [Linear pair]
∴ ∠2 = 90°
Now in right ΔABD and Δ ACD,
Hyp. AB = Hyp. AC [Given]
Side AD = Ad [Common]
∴ By the Right angle - Hypotenuse - Side criterion of congruence, we have
Δ ABD ≅ ΔACD [RHS criterion of congruence]
The corresponding parts of the congruent triangles are congruent.
∴ BD = DC [c.p.c.t]
Hence D is the mid point of BC.
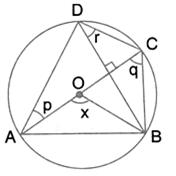
Solution 5
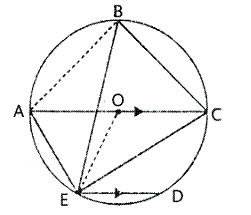
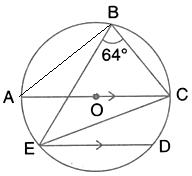
Join OE.
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∠EOC = 2 ∠EBC = 2 × 65° = 130°.
Now in Δ OEC, OE = OC [Radii of the same circle]
∴ ∠OEC = ∠OCE
But, in Δ EOC,
∠OEC + ∠OCE + ∠EOC = 180° [Angles of a triangle]
⇒ ∠OCE + ∠OCE + ∠EOC = 180°
⇒ 2 ∠OCE + 130° = 180°
⇒ 2 ∠OCE = 180° - 130°
⇒ 2 ∠OCE + 50°
⇒ ∠OCE = 
= 25°
∴ AC || ED [given]
∴ ∠DEC = ∠OCE [Alternate angles]
⇒ ∠DEC = 25°
Solution 6
Solution 7
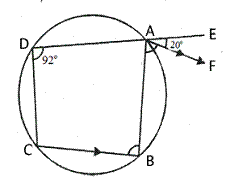
Solution 8
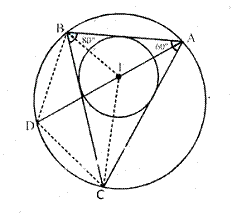
Solution 9
Solution 10
Solution 11
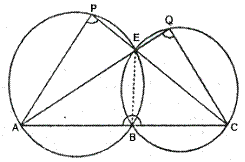
Solution 12
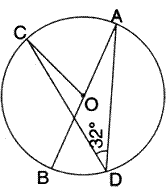
Solution 13
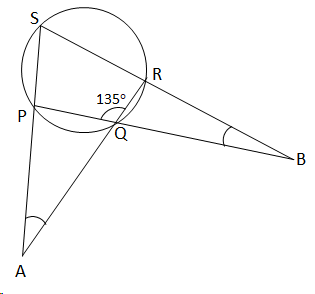
Solution 14
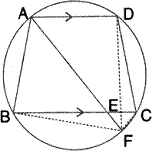
Solution 15
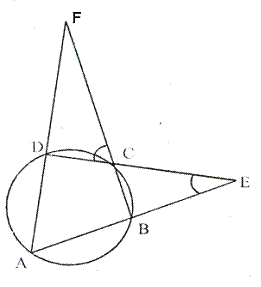
Solution 16
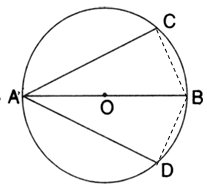
Solution 17
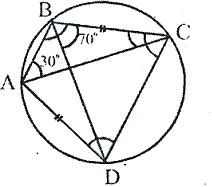
Solution 18
Solution 19
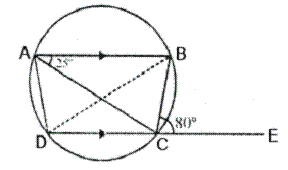
Solution 20
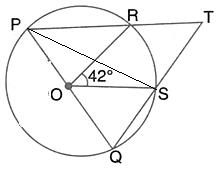
Given - In the figure, CP is the bisector of ∠ABC
To prove - DP is the bisector of ∠ADB
Proof - Since CP is the bisector of ∠ACB
∴ ∠ACP = ∠BCP
But ∠ACP = ∠ADP [Angles in the same segment of the circle]
and ∠BCP = ∠BDP
But ∠ACP = ∠BCP
∴ ∠ADP = ∠BDP
∴ DP is the bisector of ∠ADB
Solution 21
Solution 22
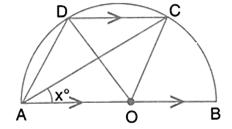
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.
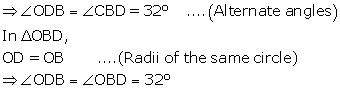
Solution 23
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∴∠DAB = 110°
Also,
∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC
∴∠BCD = 70°
∠BCD = 
∠BOD…angles subtended by an arc on the center and on the circle
∴∠BOD = 140°
In ΔBOD,
OB = OD……radii of same circle
So,
∠OBD =∠ODB……isosceles triangle theorem
∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle
2∠OBD = 40°
∠OBD = 20°
