Class 10 SELINA Solutions Maths Chapter 10 - Arithmetic Progression
Arithmetic Progression Exercise Ex. 10(A)
Solution 2
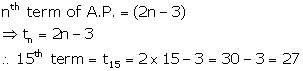
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11
The given A.P. is 1, 4, 7, 10, ……….
Solution 12
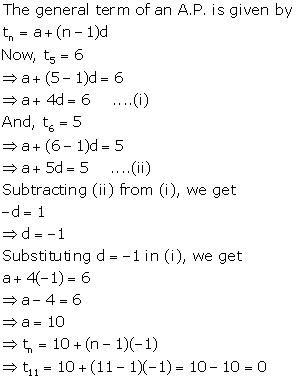
Solution 13

Solution 14

Solution 15

Solution 16
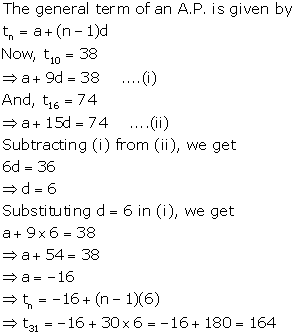
Solution 17

Solution 18
For a given A.P.,
Number of terms, n = 60
First term, a = 7
Last term, l = 125
⇒ t60 = 125
⇒ a + 59d = 125
⇒ 7 + 59d = 125
⇒ 59d = 118
⇒ d = 2
Hence, t31 = a + 30d = 7 + 30(2) = 7 + 60 = 67
Solution 19
Let 'a' be the first term and 'd' be the common difference of the given A.P.
t4 + t8 = 24 (given)
⇒ (a + 3d) + (a + 7d) = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ….(i)
And,
t6 + t10 = 34 (given)
⇒ (a + 5d) + (a + 9d) = 34
⇒ 2a + 14d = 34
⇒ a + 7d = 17 ….(ii)
Subtracting (i) from (ii), we get
2d = 5
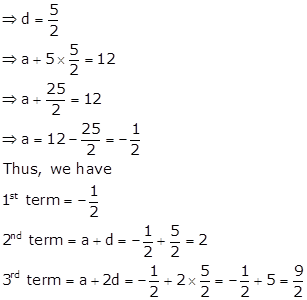
Solution 20
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Now, t3 = 5 (given)
⇒ a + 2d = 5 ….(i)
And,
t7 = 9 (given)
⇒ a + 6d = 9 ….(ii)
Subtracting (i) from (ii), we get
4d = 4
⇒ d = 1
⇒ a + 2(1) = 5
⇒ a = 3
Hence, 17th term = t17 = a + 16d = 3 + 16(1) = 19
Arithmetic Progression Exercise Ex. 10(B)
Solution 2

Solution 3

Solution 4

Solution 5
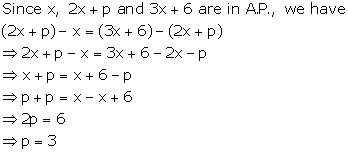
Solution 6

Solution 7

Solution 8
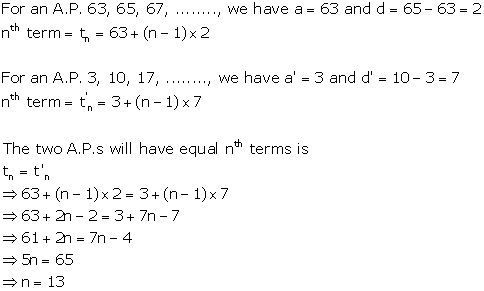
Solution 9

Solution 10
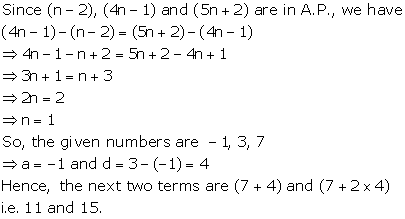
Solution 11
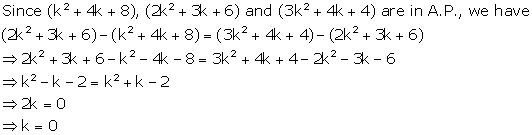
Solution 12

Solution 13
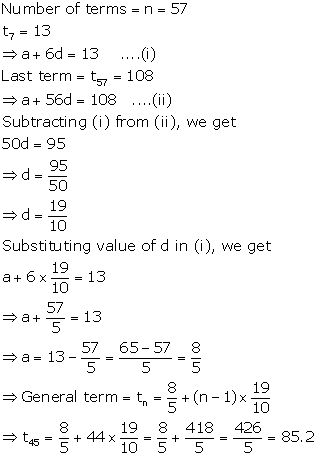
Solution 14

Solution 15

Solution 16
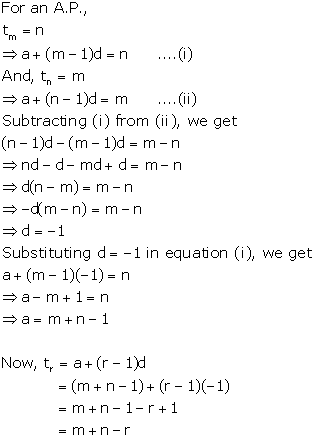
Solution 17

Arithmetic Progression Exercise Ex. 10(C)
Solution 2
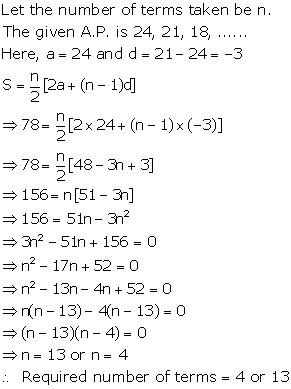
Solution 3

Solution 4(i)

Solution 4(ii)

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
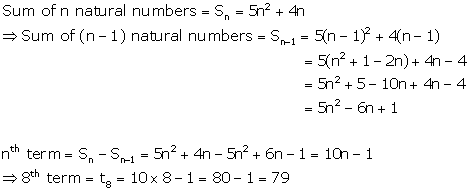
Solution 13

Arithmetic Progression Exercise Ex. 10(D)
Solution 2
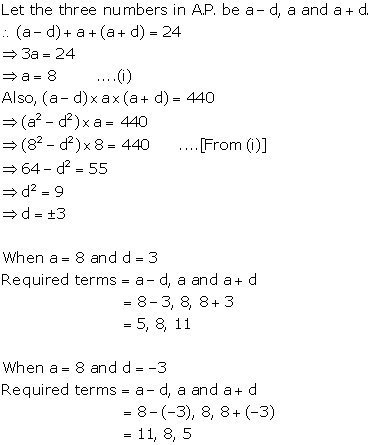
Solution 3

Solution 4

Solution 5
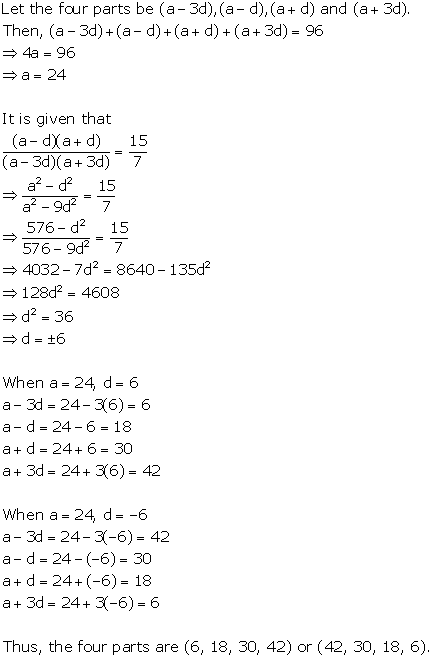
Solution 6
We know that,
Sum of n terms of an A.P = ![]()
Let the first term be 2x and the last term be 3x.
∴ Sum of 5 terms of an A.P = ![]()
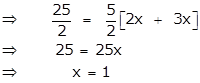
First term = 2x =2 × 1 = 2 and the last term = 3x = 3 × 1 = 3
nth term of an A.P. is given by
tn = a + (n - 1)d
⇒ a5 = 2 + (5 - 1)d
⇒ 3 = 2 + 4d
⇒ 1 = 4d
⇒ d = ![]() = 0.25
= 0.25
Therefore the five numbers in an A.P are 2, 2.25, 2.50, 2.75 and 3.
Solution 7

Solution 8
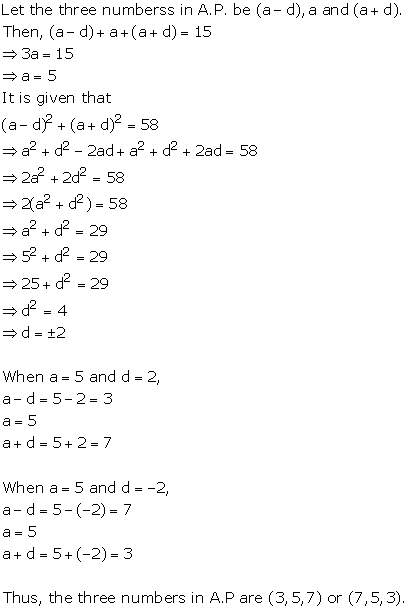
Solution 9
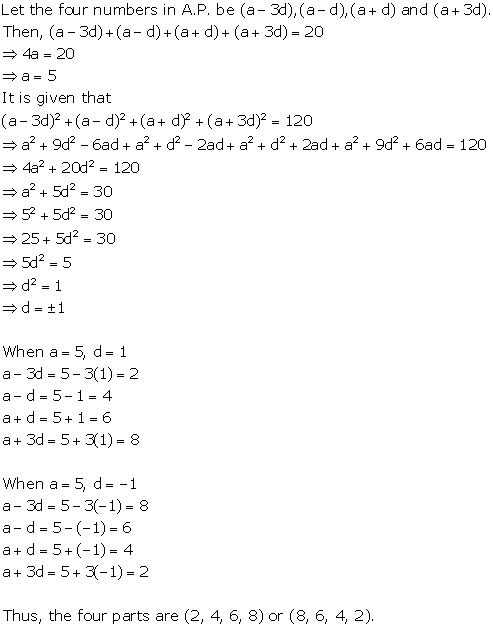
Solution 10
![]()
Solution 11

Solution 12
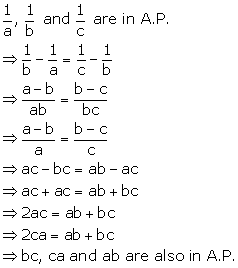
Arithmetic Progression Exercise TEST YOURSELF
Solution 2
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Now, t6 = 16 (given)
⇒ a + 5d = 16 ….(i)
And,
t14 = 32 (given)
⇒ a + 13d = 32 ….(ii)
Subtracting (i) from (ii), we get
8d = 16
⇒ d = 2
⇒ a + 5(2) = 16
⇒ a = 6
Hence, 36th term = t36 = a + 35d = 6 + 35(2) = 76
Solution 3

Solution 4
For a given A.P.,
Number of terms, n = 50
3rd term, t3 = 12
⇒ a + 2d = 12 ….(i)
Last term, l = 106
⇒ t50 = 106
⇒ a + 49d = 106 ….(ii)
Subtracting (i) from (ii), we get
47d = 94
⇒ d = 2
⇒ a + 2(2) = 12
⇒ a = 8
Hence, t29 = a + 28d = 8 + 28(2) = 8 + 56 = 64
Solution 5
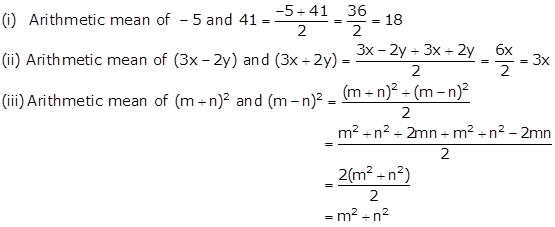
Solution 6
Here,
First term, a = 3
Last term, l = 57
n = 20
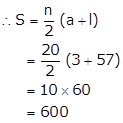
Solution 7
Here, we find that
15 - 18 = 12 - 15 = -3
Thus, the given series is an A.P. with first term 18 and common difference -3.
Let the number of term to be added be 'n'.
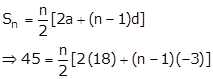
⇒ 90 = n[36 - 3n + 3]
⇒ 90 = n[39 - 3n]
⇒ 90 = 3n[13 - n]
⇒ 30 = 13n - n2
⇒ n2 - 13n + 30 = 0
⇒ n2 - 10n - 3n + 30 = 0
⇒ n(n - 10) - 3(n - 10) = 0
⇒ (n - 10)(n - 3) = 0
⇒ n - 10 = 0 or n - 3 = 0
⇒ n = 10 or n = 3
Thus, required number of term to be added is 3 or 10.
Solution 8
tn = 8 - 5n
Replacing n by (n + 1), we get
tn+1 = 8 - 5(n + 1) = 8 - 5n - 5 = 3 - 5n
Now,
tn+1 - tn = (3 - 5n) - (8 - 5n) = -5
Since, (tn+1 - tn) is independent of n and is therefore a constant.
Hence, the given sequence is an A.P.
Solution 9
The given sequence is 1, -1, -3, …..
Now,
1 - 3 = -1 - 1 = -3 - (-1) = -2
Hence, the given sequence is an A.P. with first term a = 3 and common difference d = -2.
The general term (nth term) of an A.P. is given by
tn = a + (n - 1)d
= 3 + (n - 1)(-2)
= 3 - 2n + 2
= 5 - 2n
Hence, 23rd term = t23 = 5 - 2(23) = 5 - 46 = -41
Solution 10
The given sequence is 11, 8, 5, 2, …..
Now,
8 - 11 = 5 - 8 = 2 - 5 = -3
Hence, the given sequence is an A.P. with first term a = 11 and common difference d = -3.
The general term of an A.P. is given by
tn = a + (n - 1)d
⇒ -150 = 11 + (n - 1)(-5)
⇒ -161 = -5n + 5
⇒ 5n = 166
![]()
The number of terms cannot be a fraction.
So, clearly, -150 is not a term of the given sequence.
Solution 11

Solution 12

Solution 13
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Given,
S14 = 1050
![]()
⇒ 7[2a + 13d] = 1050
⇒ 2a + 13d = 150
⇒ a + 6.5d = 75 ….(i)
And, t14 = 140
⇒ a + 13d = 140 ….(ii)
Subtracting (i) from (ii), we get
6.5d = 65
⇒ d = 10
⇒ a + 13(10) = 140
⇒ a = 10
Thus, 20th term = t20 = 10 + 19d = 10 + 19(10) = 200
Solution 14
nth term of an A.P. is given by tn= a + (n - 1) d.
⇒ t25 = a + (25 - 1)d = a + 24d and
t9 = a + (9 - 1)d = a + 8d
According to the condition in the question, we get
t25 = t9 + 16
⇒ a + 24d = a + 8d + 16
⇒ 16d = 16
⇒ d = 1
Solution 15
Let a and d be the first term and common difference respectively.
⇒(m + n)th term = a + (m + n - 1)d …. (i) and
(m - n)th term = a + (m - n - 1)d …. (ii)
From (i) + (ii), we get
(m + n)th term + (m - n)th term
= a + (m + n - 1)d + a + (m - n - 1)d
= a + md + nd - d + a + md - nd - d
= 2a + 2md - 2d
= 2a + (m - 1)2d
= 2[ a + (m - 1)d]
= 2 × mthterm
Hence proved.
Solution 16
In the first A.P. 58, 60, 62,....
a = 58 and d = 2
tn = a + (n - 1)d
⇒ tn = 58 + (n - 1)2 …. (i)
In the first A.P. -2, 5, 12, ….
a = -2 and d = 7
tn = a + (n - 1)d
⇒ tn= -2 + (n - 1)7 …. (ii)
Given that the nth term of first A.P is equal to the nth term of the second A.P.
⇒58 + (n - 1)2 = -2 + (n - 1)7 … from (i) and (ii)
⇒58 + 2n - 2 = -2 + 7n - 7
⇒ 65 = 5n
⇒ n = 15
Solution 17
Here a = 105 and d = 101 - 105 = -4
Let an be the first negative term.
⇒ an < 0
⇒ a + (n - 1)d < 0
⇒ 105 + (n - 1)(-4)<0
⇒ 105 - 4n + 4 <0
⇒ 109 - 4n < 0
⇒ 109 <4n
⇒ 27.25 < n
The value of n = 28.
Therefore 28th term is the first negative term of the given A.P.
Solution 18
Let the three parts of 216 in A.P be (a - d), a, (a + d).
⇒a - d + a + a + d = 216
⇒ 3a = 216
⇒ a = 72
Given that the product of the two smaller parts is 5040.
⇒a(a - d ) = 5040
⇒ 72(72 - d) = 5040
⇒ 72 - d = 70
⇒ d = 2
∴ a - d = 72 - 2 = 70, a = 72 and a + d = 72 + 2 = 74
Therefore the three parts of 216 are 70, 72 and 74.
Solution 19
We have 2n2 - 7,
Substitute n = 1, 2, 3, … , we get
2(1)2 - 7, 2(2)2 - 7, 2(3)2 - 7, 2(4)2 - 7, ….
-5, 1, 11, ….
Difference between the first and second term = 1 - (-5) = 6
And Difference between the second and third term = 11 - 1 = 10
Here, the common difference is not same.
Therefore the nth term of an A.P can't be 2n2 - 7.
Solution 20
Here a = 14 , d = 7 and tn = 168
tn = a + (n - 1)d
⇒ 168 = 14 + (n - 1)7
⇒ 154 = 7n - 7
⇒ 154 = 7n - 7
⇒ 161 = 7n
⇒ n = 23
We know that,

Therefore the sum of the A.P., 14, 21, 28, …, 168 is 2093.
Solution 21
Here a = 20 and S7 = 2100
We know that,
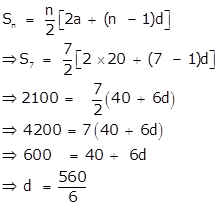
To find: t31 =?
tn = a + (n - 1)d
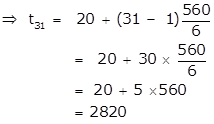
Therefore the 31st term of the given A.P. is 2820.
Solution 22
First we will reverse the given A.P. as we have to find the sum of last 8 terms of the A.P.
58, …., -8, -10, -12.
Here a = 58 , d = -2
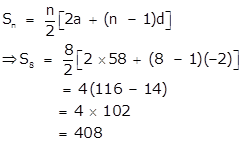
Therefore the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58 is 408.


